高中数学人教A版必修第一册 3.2.2奇偶性 课件 (共23张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册 3.2.2奇偶性 课件 (共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 21:56:36 | ||
图片预览






文档简介
(共23张PPT)
第3章 函数的概念与性质
3.2.2 函数的奇偶性
人教A版2019高中数学必修第一册
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上“上升”(或“下降” )的性质.
现在继续研究函数的奇偶性.
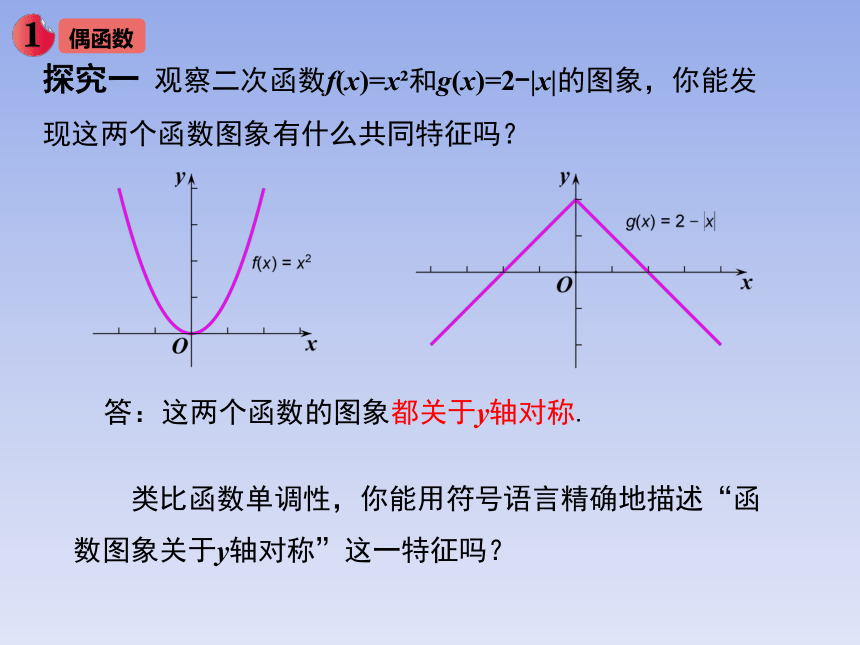
探究一 观察二次函数f(x)=x 和g(x)=2-|x|的图象,你能发现这两个函数图象有什么共同特征吗?
答:这两个函数的图象都关于y轴对称.
类比函数单调性,你能用符号语言精确地描述“函数图象关于y轴对称”这一特征吗?
偶函数
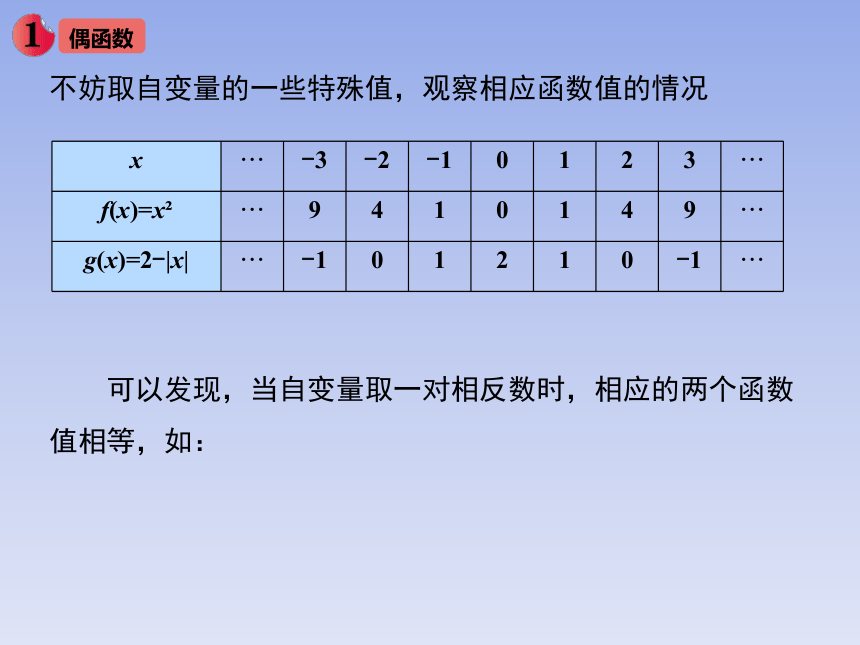
不妨取自变量的一些特殊值,观察相应函数值的情况
可以发现,当自变量取一对相反数时,相应的两个函数值相等,如:
x ··· -3 -2 -1 0 1 2 3 ···
f(x)=x ··· 9 4 1 0 1 4 9 ···
g(x)=2-|x| ··· -1 0 1 2 1 0 -1 ···
偶函数
对于函数f(x)=x ,有
f(-3)=9= f(3);
f(-2)=4= f(2);
f(-1)=1= f(1);
同样,对于函数g(x)=2-|x| ,有
g(-1)=2-|-1|=1= g(1);
g(-2)=2-|-2|=0= g(2);
g(-3)=2-|-3|=-1= g(3)······
偶函数
实际上, x∈R,都有f(-x)=(-x) =x =f(x),这时称函数f(x)=x 为偶函数.
同样, x∈R,都有g(-x)=2-|-x|=2-|x|=g(x),这时称函数g(x)=2-|x|为偶函数.
偶函数
偶函数
画出函数 和函数 的图像并观察,你能发现什么共
同的特征?
可以发现,这两个函数都关于y轴对称.也就是说,当自变量取互为相反数的
两个数时,函数值是相等的,即
对于 ,有
对于 ,有
常见的偶函数有 , 等等
偶函数
【定义】一般地,设函数 的定义域为A,如果对于 ,都有 ,
且 ,即 的图像关于y轴对称,那么就称 为偶函数.
【思考】对于定义在R上的函数 ,若 ,那么这个函数
是偶函数吗?
【答】不一定.因为 并不能保证所有的 ,所
以不一定是偶函数.
要证明某个函数不是偶函数,只需要列举出一个反例x0,证明f(-x0)≠f(x0)即可
【1】①该函数的定义域关于y轴对称,即任意x∈A(A为定义域),-x∈A;
②任取一个自变量x,都满足f(-x)=f(x)
偶函数
【总结】一般地,一个函数是偶函数的两个判断方式:
【2】几何法,函数的图像关于y轴对称,那么函数就是偶函数
偶函数
偶函数
图像关于y轴对称
代数特征
几何特征
定义中, 的常见变形有:
画出函数 和函数 的图像并观察,你能发现什么共
同的特征?
奇函数
可以发现,这两个函数都关于原点成中心对称.也就是说,当自变量取互为
相反数的两个数时,函数值也互为相反数,即
对于 ,有
对于 ,有
奇函数
常见的奇函数有 , , 等等
【思考】对于定义在R上的函数 ,若 ,那么这个
函数是奇函数吗?
【定义】一般地,设函数 的定义域为A,如果对于 ,都有 ,
且 , 即 的图像关于原点成中心对称,那么就称
为奇函数.
【答】不一定.因为 并不能保证所有的 ,
所以不一定是奇函数.
奇函数
要证明某个函数不是奇函数,只需要列举出一个反例x0,证明f(-x0)≠-f(x0)即可
【1】①该函数的定义域关于y轴对称,即任意x∈A(A为定义域),-x∈A;
②任取一个自变量x,都满足f(-x)=-f(x)
【总结】一般地,一个函数是奇函数的两个判断方式:
【2】几何法,函数的图像关于原点成中心对称,那么函数就是奇函数
奇函数
奇函数
图像关于原点对称
代数特征
几何特征
定义中, 的常见变形有:
如果奇函数在
处有定义,则:
如何证明
这个结论?
函数奇偶性的判断
【例题】判断下列函数的奇偶性.
【解】(1)首先判断定义域为R,关于y轴对称,再判断:
所以此函数是偶函数;
【解】(2)首先判断定义域为R,关于y轴对称,再判断:
所以此函数是奇函数;
【解】(3)首先判断定义域为 ,关于y轴对称,再判断:
所以此函数是奇函数;
【解】(3)首先判断定义域为 ,关于y轴对称,再判断:
所以此函数是偶函数.
判断函数奇偶性,首先要看定义域.
④ 既是奇函数,又是偶函数.
函数奇偶性的判断
利用定义判断函数奇偶性的方法:
【1】一看定义域:奇函数和偶函数的定义域一定关于y轴对称,如果一个函数的定
义域关于y轴对称,那么它才有可能是奇函数或者偶函数,否则就没有探究下
去的必要.
【2】二看等式:满足第一点之后,判断 与 的关系:
函数
既是奇函数,又是偶函数
① 是偶函数;
② 是奇函数;
③ 是非奇非偶函数;
奇(偶)函数的性质及应用
【探究】(1)如何判断函数 的奇偶性?
【解】(1)利用函数奇偶性定义来判断,函数
的定义域为R,且有
所以此
函数是奇函数.
(2)已知函数 图像的一部分,如何画出剩余部分?
(2)由奇函数的图像关于原点成中心对称可以画出函数 在
y轴左侧对的图像,将y轴右侧的图像沿着原点旋转180°即可,画出的
图像如图所示.
奇(偶)函数的性质及应用
【拓展】
(1)奇偶函数的单调性:
①奇函数:奇函数在y轴左右两边的单调性是完全相同的.如果
奇函数在区间[a,b]上的单调增函数,那么在区间[-a,-b]上就
是单调增函数.
②偶函数:奇函数在y轴左右两边的单调性是完全相反的.如果
偶函数在区间[a,b]上的单调增函数,那么在区间[-a,-b]上就
是单调减函数.
奇(偶)函数的性质及应用
【拓展】(2)奇偶函数的运算性质及符合函数的奇偶性:
设 , 的定义域分别是A和B,在公共定义域上有:
【注】上表中不考虑 和 的情况;
中需 , .
偶
偶
偶
偶
奇
奇
奇
奇
偶
奇
偶
奇
偶
奇
偶
奇
偶
偶
偶
奇
Thank you for watching !
第3章 函数的概念与性质
3.2.2 函数的奇偶性
人教A版2019高中数学必修第一册
前面我们用符号语言精确地描述了函数图象在定义域的某个区间上“上升”(或“下降” )的性质.
现在继续研究函数的奇偶性.
探究一 观察二次函数f(x)=x 和g(x)=2-|x|的图象,你能发现这两个函数图象有什么共同特征吗?
答:这两个函数的图象都关于y轴对称.
类比函数单调性,你能用符号语言精确地描述“函数图象关于y轴对称”这一特征吗?
偶函数
不妨取自变量的一些特殊值,观察相应函数值的情况
可以发现,当自变量取一对相反数时,相应的两个函数值相等,如:
x ··· -3 -2 -1 0 1 2 3 ···
f(x)=x ··· 9 4 1 0 1 4 9 ···
g(x)=2-|x| ··· -1 0 1 2 1 0 -1 ···
偶函数
对于函数f(x)=x ,有
f(-3)=9= f(3);
f(-2)=4= f(2);
f(-1)=1= f(1);
同样,对于函数g(x)=2-|x| ,有
g(-1)=2-|-1|=1= g(1);
g(-2)=2-|-2|=0= g(2);
g(-3)=2-|-3|=-1= g(3)······
偶函数
实际上, x∈R,都有f(-x)=(-x) =x =f(x),这时称函数f(x)=x 为偶函数.
同样, x∈R,都有g(-x)=2-|-x|=2-|x|=g(x),这时称函数g(x)=2-|x|为偶函数.
偶函数
偶函数
画出函数 和函数 的图像并观察,你能发现什么共
同的特征?
可以发现,这两个函数都关于y轴对称.也就是说,当自变量取互为相反数的
两个数时,函数值是相等的,即
对于 ,有
对于 ,有
常见的偶函数有 , 等等
偶函数
【定义】一般地,设函数 的定义域为A,如果对于 ,都有 ,
且 ,即 的图像关于y轴对称,那么就称 为偶函数.
【思考】对于定义在R上的函数 ,若 ,那么这个函数
是偶函数吗?
【答】不一定.因为 并不能保证所有的 ,所
以不一定是偶函数.
要证明某个函数不是偶函数,只需要列举出一个反例x0,证明f(-x0)≠f(x0)即可
【1】①该函数的定义域关于y轴对称,即任意x∈A(A为定义域),-x∈A;
②任取一个自变量x,都满足f(-x)=f(x)
偶函数
【总结】一般地,一个函数是偶函数的两个判断方式:
【2】几何法,函数的图像关于y轴对称,那么函数就是偶函数
偶函数
偶函数
图像关于y轴对称
代数特征
几何特征
定义中, 的常见变形有:
画出函数 和函数 的图像并观察,你能发现什么共
同的特征?
奇函数
可以发现,这两个函数都关于原点成中心对称.也就是说,当自变量取互为
相反数的两个数时,函数值也互为相反数,即
对于 ,有
对于 ,有
奇函数
常见的奇函数有 , , 等等
【思考】对于定义在R上的函数 ,若 ,那么这个
函数是奇函数吗?
【定义】一般地,设函数 的定义域为A,如果对于 ,都有 ,
且 , 即 的图像关于原点成中心对称,那么就称
为奇函数.
【答】不一定.因为 并不能保证所有的 ,
所以不一定是奇函数.
奇函数
要证明某个函数不是奇函数,只需要列举出一个反例x0,证明f(-x0)≠-f(x0)即可
【1】①该函数的定义域关于y轴对称,即任意x∈A(A为定义域),-x∈A;
②任取一个自变量x,都满足f(-x)=-f(x)
【总结】一般地,一个函数是奇函数的两个判断方式:
【2】几何法,函数的图像关于原点成中心对称,那么函数就是奇函数
奇函数
奇函数
图像关于原点对称
代数特征
几何特征
定义中, 的常见变形有:
如果奇函数在
处有定义,则:
如何证明
这个结论?
函数奇偶性的判断
【例题】判断下列函数的奇偶性.
【解】(1)首先判断定义域为R,关于y轴对称,再判断:
所以此函数是偶函数;
【解】(2)首先判断定义域为R,关于y轴对称,再判断:
所以此函数是奇函数;
【解】(3)首先判断定义域为 ,关于y轴对称,再判断:
所以此函数是奇函数;
【解】(3)首先判断定义域为 ,关于y轴对称,再判断:
所以此函数是偶函数.
判断函数奇偶性,首先要看定义域.
④ 既是奇函数,又是偶函数.
函数奇偶性的判断
利用定义判断函数奇偶性的方法:
【1】一看定义域:奇函数和偶函数的定义域一定关于y轴对称,如果一个函数的定
义域关于y轴对称,那么它才有可能是奇函数或者偶函数,否则就没有探究下
去的必要.
【2】二看等式:满足第一点之后,判断 与 的关系:
函数
既是奇函数,又是偶函数
① 是偶函数;
② 是奇函数;
③ 是非奇非偶函数;
奇(偶)函数的性质及应用
【探究】(1)如何判断函数 的奇偶性?
【解】(1)利用函数奇偶性定义来判断,函数
的定义域为R,且有
所以此
函数是奇函数.
(2)已知函数 图像的一部分,如何画出剩余部分?
(2)由奇函数的图像关于原点成中心对称可以画出函数 在
y轴左侧对的图像,将y轴右侧的图像沿着原点旋转180°即可,画出的
图像如图所示.
奇(偶)函数的性质及应用
【拓展】
(1)奇偶函数的单调性:
①奇函数:奇函数在y轴左右两边的单调性是完全相同的.如果
奇函数在区间[a,b]上的单调增函数,那么在区间[-a,-b]上就
是单调增函数.
②偶函数:奇函数在y轴左右两边的单调性是完全相反的.如果
偶函数在区间[a,b]上的单调增函数,那么在区间[-a,-b]上就
是单调减函数.
奇(偶)函数的性质及应用
【拓展】(2)奇偶函数的运算性质及符合函数的奇偶性:
设 , 的定义域分别是A和B,在公共定义域上有:
【注】上表中不考虑 和 的情况;
中需 , .
偶
偶
偶
偶
奇
奇
奇
奇
偶
奇
偶
奇
偶
奇
偶
奇
偶
偶
偶
奇
Thank you for watching !
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
