高中数学人教A版必修第一册课件 3.2.2奇偶性 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件 3.2.2奇偶性 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 21:57:00 | ||
图片预览





文档简介
(共19张PPT)
1.3.2函数的奇偶性
必修1(人教A版)
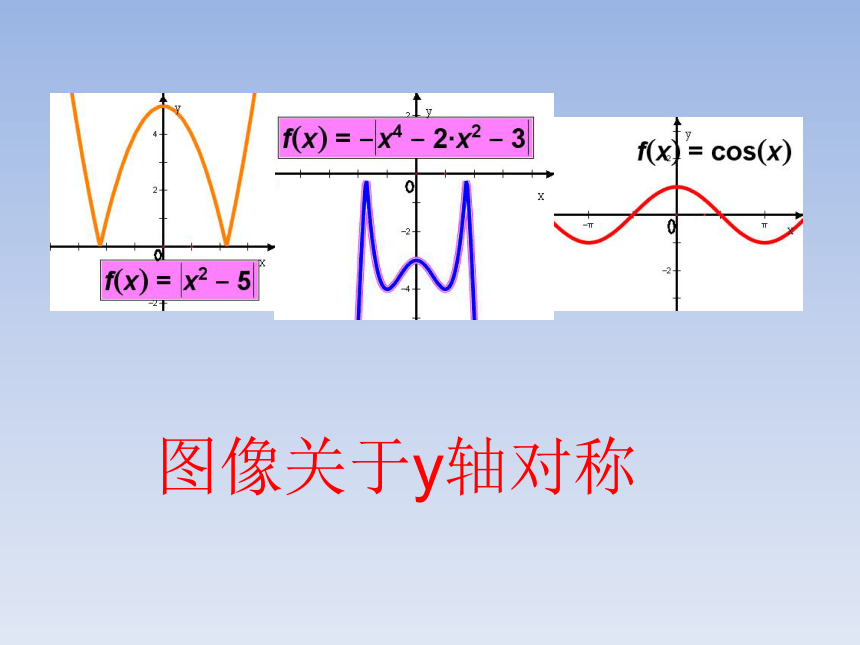
如果我们将以上图形放在坐标系中,观察这些图像,看哪个小组能说出它们有什么共同的特征?(抢答)
图像关于y轴对称
……
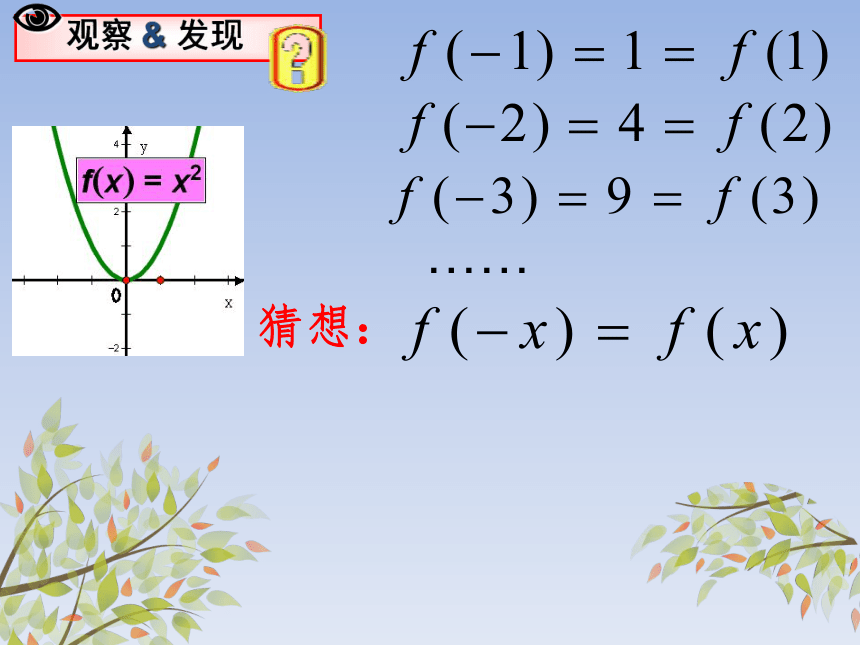
观察 & 发现
猜想:
我发现
【甄别】判断:
(1)若 则 是偶函数;
(2)若对于定义域内的一些 ,使 则 是偶函数;
(3)若 则 不是偶函数。
对于定义在 上的函数 ,
偶函数的定义
把图像关于原点对称函数称为奇函数
x ... -3 -2 -1 0 1 2 3 ...
f(x) ... ...
猜想:
… ...
类比&探究
x ... -3 -2 -1 0 1 2 3 ...
f(x) ... -27 -8 -1 0 1 8 27 ...
奇函数的定义
及时梳理
例1:根据图像判断函数是否为偶函数
思考&探究
具有奇偶性的函数,
其定义域在数轴上有怎样的特点?
具有奇偶性的函数,
其定义域关于原点对称。
思考一
如何根据定义判断函数的奇偶性?
(1)先看函数定义域,并判断定义域是否关于原点对称;
(2)计算f(-x)并化简
(3) 判断f(x)与f(-x)的关系;
若f(-x)=f(x),则f(x)是偶函数;
若f(-x)= - f(x),则f(x)是奇函数.
思考二
简记为:一看二算三判断
例2.判断下列函数的奇偶性:
1.本节课知识上有哪些收获?
2.本节课使用了那些数学思想?
3.做题过程中形成了那些数学素养?
4.本节课使用那些解决问题的方法?
5.你发现了数学中的那些美?
函数奇偶很对称, 式子关系别搞混, 判断步骤是什么, 一看二算三判断.
作业:
B组 判断下列函数的奇偶性
挑战老师
两人在一个足够大的圆内依次放等大圆形棋子,先超出边界着为输。老师先放一定会赢,你敢挑战吗?
1.3.2函数的奇偶性
必修1(人教A版)
如果我们将以上图形放在坐标系中,观察这些图像,看哪个小组能说出它们有什么共同的特征?(抢答)
图像关于y轴对称
……
观察 & 发现
猜想:
我发现
【甄别】判断:
(1)若 则 是偶函数;
(2)若对于定义域内的一些 ,使 则 是偶函数;
(3)若 则 不是偶函数。
对于定义在 上的函数 ,
偶函数的定义
把图像关于原点对称函数称为奇函数
x ... -3 -2 -1 0 1 2 3 ...
f(x) ... ...
猜想:
… ...
类比&探究
x ... -3 -2 -1 0 1 2 3 ...
f(x) ... -27 -8 -1 0 1 8 27 ...
奇函数的定义
及时梳理
例1:根据图像判断函数是否为偶函数
思考&探究
具有奇偶性的函数,
其定义域在数轴上有怎样的特点?
具有奇偶性的函数,
其定义域关于原点对称。
思考一
如何根据定义判断函数的奇偶性?
(1)先看函数定义域,并判断定义域是否关于原点对称;
(2)计算f(-x)并化简
(3) 判断f(x)与f(-x)的关系;
若f(-x)=f(x),则f(x)是偶函数;
若f(-x)= - f(x),则f(x)是奇函数.
思考二
简记为:一看二算三判断
例2.判断下列函数的奇偶性:
1.本节课知识上有哪些收获?
2.本节课使用了那些数学思想?
3.做题过程中形成了那些数学素养?
4.本节课使用那些解决问题的方法?
5.你发现了数学中的那些美?
函数奇偶很对称, 式子关系别搞混, 判断步骤是什么, 一看二算三判断.
作业:
B组 判断下列函数的奇偶性
挑战老师
两人在一个足够大的圆内依次放等大圆形棋子,先超出边界着为输。老师先放一定会赢,你敢挑战吗?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
