高中数学人教A版必修第一册课件 3.2函数的表示方法 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件 3.2函数的表示方法 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 21:57:54 | ||
图片预览





文档简介
(共19张PPT)
3.1.2函数的表示法
下列各组函数中是不是同一个函数?
否
否
否
是
是
判断两个函数是否表示同一个函数的方法步骤:
(1)先求两个函数的定义域,如果定义域不同,那么它们是不同的函数。如果定义域相同,则进行第2步
(2)化简函数解析式,如果化简后的解析式相同,那么它们是同一个函数,否则不是同一个函数。
即:判定两个函数是否相同,只需考察对应关系(表达式)与定义域是否相同即可。
问题4:恩格尔系数
列表法
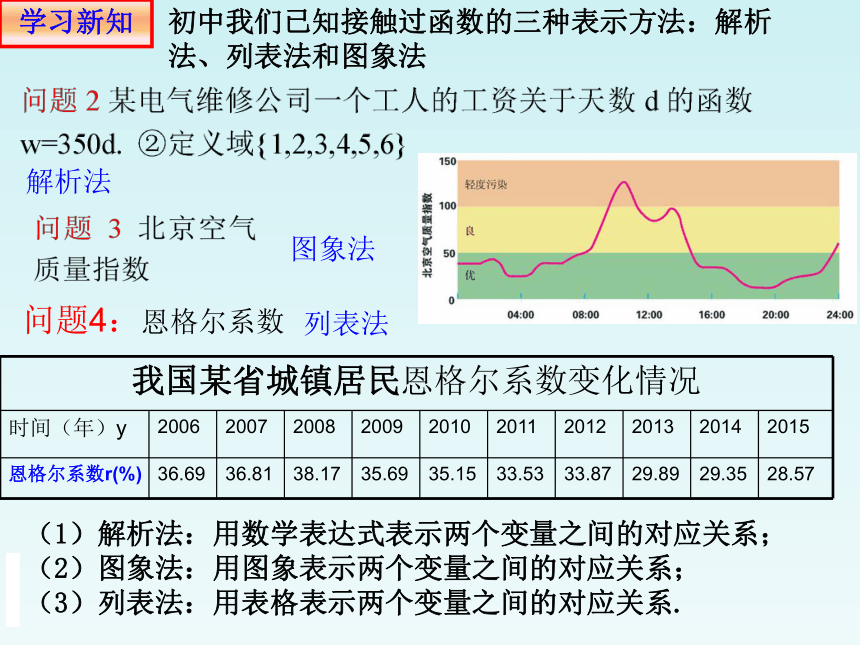
学习新知
初中我们已知接触过函数的三种表示方法:解析法、列表法和图象法
解析法
(1)解析法:用数学表达式表示两个变量之间的对应关系;
(2)图象法:用图象表示两个变量之间的对应关系;
(3)列表法:用表格表示两个变量之间的对应关系.
图象法
我国某省城镇居民恩格尔系数变化情况
时间(年)y 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
恩格尔系数r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35 28.57
解析法
y=5x
注:用解析法必须注明函数的定义域。
列表法
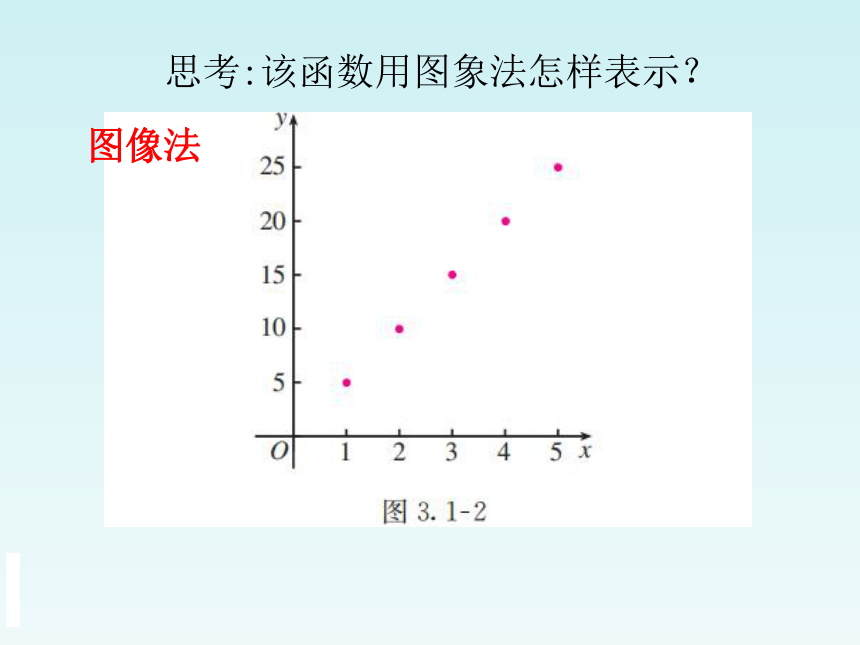
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
典型例题
思考:该函数用图象法怎样表示?
图像法
三种表示方法的特点
列表法的特点:不通过计算就可以直接看出与自变量的值相对应的函数值。
图像法的特点:直观形象地表示出函数的变化情况 ,有利于通过图形研究函数的某些性质。
学习新知
解析法的特点:全面.精确地概括了变量间的关系;可以通过用解析式求出任意一个自变量所对应的函数值。
1 设周长为20cm的矩形的一边长为xcm,面积为Scm2,那么x与S的对应关系是否为函数?若是,试用适当的方法表示出来.
所有的函数都能用三种方法表示吗
解:由绝对值的概念,我们有
注:我们把这样的函数叫做: 分段函数分段函数是一个函数,自变量所在区间变化,对应关系也随之变化。
例2.画出函数y=|x|的图象
典型例题
所以函数y=|x|的图象如右图所示
1. 分段函数是一个函数,不要把它误认为是“几个函数”;
2. 有些函数既可用列表法表示,也可用图像法或解析法表示.
注意
练习1:画出函数y=|x-2|的图像
针对练习
练习2:画函数y=|x -1|的图像
典型例题
典型例题
信函质量(m)/g
邮资(M)/元
0.80
1.60
2.40
3.20
4.00
1.国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如下表:
请画出图像,并写出函数的解析式.
巩固练习
解:邮资是信函质量的函数, 其图像如下:
20
M/元
m/g
40
60
80
100
0.8
1.6
2.4
3.2
4.0
。
。
。
。
。
O
函数解析式为
0.8, 01.60, 20M= 2.40, 403.20, 604.00, 802.某质点在30s内运动速度vcm/s是时间t的函数,它的图像如右图.用解析式表示出这个函数, 并求出9s时质点的速度.
10
20
30
10
30
v
t
O
巩固练习
t=9s时,v(9)=3×9=27 (cm/s)
解: 解析式为v (t)=
t+10, (0 ≤ t<5)
3t, (5 ≤ t<10)
30, ( 10 ≤t <20)
-3t+90,(20 ≤ t≤30)
3. 已知函数f (x)=
2x+3, x<-1,
x2, -1≤x<1,
x-1, x≥1 .
求f{f[f(-2)]}
解: (1) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
巩固练习
(2) 当f (x)=-7时,求x ;
(2)若x<-1 , 2x+3 <1,与f (x)=-7相符,
由2x+3 =-7得x=-5
易知其他二段均不符合f (x)=-7 。
故 x=-5
4.课本p69 : 1
5.以下叙述正确的有( )
(1)分段函数的定义域是各段定义域的并集。值域是各段值域的并集。
(2)分段函数在定义域的不同部分有不同的对应法则,但它是一个函数。
(3)若D1、D2分别是分段函数的两个不同对应法则的值域,则D1∩ D2 ≠φ也能成立。
A 1个 B 2个 C 3个 D 0个
C
巩固练习
深化练习
自主学习
阅读课本第69页和第70页的例7,例8完成课本第71页练习
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表
示法来 表示函数;
(3)注意分段函数的表示方法及其图象的画法。
课堂小结
3.1.2函数的表示法
下列各组函数中是不是同一个函数?
否
否
否
是
是
判断两个函数是否表示同一个函数的方法步骤:
(1)先求两个函数的定义域,如果定义域不同,那么它们是不同的函数。如果定义域相同,则进行第2步
(2)化简函数解析式,如果化简后的解析式相同,那么它们是同一个函数,否则不是同一个函数。
即:判定两个函数是否相同,只需考察对应关系(表达式)与定义域是否相同即可。
问题4:恩格尔系数
列表法
学习新知
初中我们已知接触过函数的三种表示方法:解析法、列表法和图象法
解析法
(1)解析法:用数学表达式表示两个变量之间的对应关系;
(2)图象法:用图象表示两个变量之间的对应关系;
(3)列表法:用表格表示两个变量之间的对应关系.
图象法
我国某省城镇居民恩格尔系数变化情况
时间(年)y 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
恩格尔系数r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35 28.57
解析法
y=5x
注:用解析法必须注明函数的定义域。
列表法
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
典型例题
思考:该函数用图象法怎样表示?
图像法
三种表示方法的特点
列表法的特点:不通过计算就可以直接看出与自变量的值相对应的函数值。
图像法的特点:直观形象地表示出函数的变化情况 ,有利于通过图形研究函数的某些性质。
学习新知
解析法的特点:全面.精确地概括了变量间的关系;可以通过用解析式求出任意一个自变量所对应的函数值。
1 设周长为20cm的矩形的一边长为xcm,面积为Scm2,那么x与S的对应关系是否为函数?若是,试用适当的方法表示出来.
所有的函数都能用三种方法表示吗
解:由绝对值的概念,我们有
注:我们把这样的函数叫做: 分段函数分段函数是一个函数,自变量所在区间变化,对应关系也随之变化。
例2.画出函数y=|x|的图象
典型例题
所以函数y=|x|的图象如右图所示
1. 分段函数是一个函数,不要把它误认为是“几个函数”;
2. 有些函数既可用列表法表示,也可用图像法或解析法表示.
注意
练习1:画出函数y=|x-2|的图像
针对练习
练习2:画函数y=|x -1|的图像
典型例题
典型例题
信函质量(m)/g
邮资(M)/元
0.80
1.60
2.40
3.20
4.00
1.国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如下表:
请画出图像,并写出函数的解析式.
巩固练习
解:邮资是信函质量的函数, 其图像如下:
20
M/元
m/g
40
60
80
100
0.8
1.6
2.4
3.2
4.0
。
。
。
。
。
O
函数解析式为
0.8, 0
10
20
30
10
30
v
t
O
巩固练习
t=9s时,v(9)=3×9=27 (cm/s)
解: 解析式为v (t)=
t+10, (0 ≤ t<5)
3t, (5 ≤ t<10)
30, ( 10 ≤t <20)
-3t+90,(20 ≤ t≤30)
3. 已知函数f (x)=
2x+3, x<-1,
x2, -1≤x<1,
x-1, x≥1 .
求f{f[f(-2)]}
解: (1) f{f[f(-2)]} = f{f[-1]}
= f{1} =0
巩固练习
(2) 当f (x)=-7时,求x ;
(2)若x<-1 , 2x+3 <1,与f (x)=-7相符,
由2x+3 =-7得x=-5
易知其他二段均不符合f (x)=-7 。
故 x=-5
4.课本p69 : 1
5.以下叙述正确的有( )
(1)分段函数的定义域是各段定义域的并集。值域是各段值域的并集。
(2)分段函数在定义域的不同部分有不同的对应法则,但它是一个函数。
(3)若D1、D2分别是分段函数的两个不同对应法则的值域,则D1∩ D2 ≠φ也能成立。
A 1个 B 2个 C 3个 D 0个
C
巩固练习
深化练习
自主学习
阅读课本第69页和第70页的例7,例8完成课本第71页练习
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表
示法来 表示函数;
(3)注意分段函数的表示方法及其图象的画法。
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
