高中数学人教A版必修第一册课件 3.3幂函数 课件(共21张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件 3.3幂函数 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 22:24:36 | ||
图片预览







文档简介
(共21张PPT)
2.4幂函数与二次函数第2课时
考点一:幂函数的图像与性质
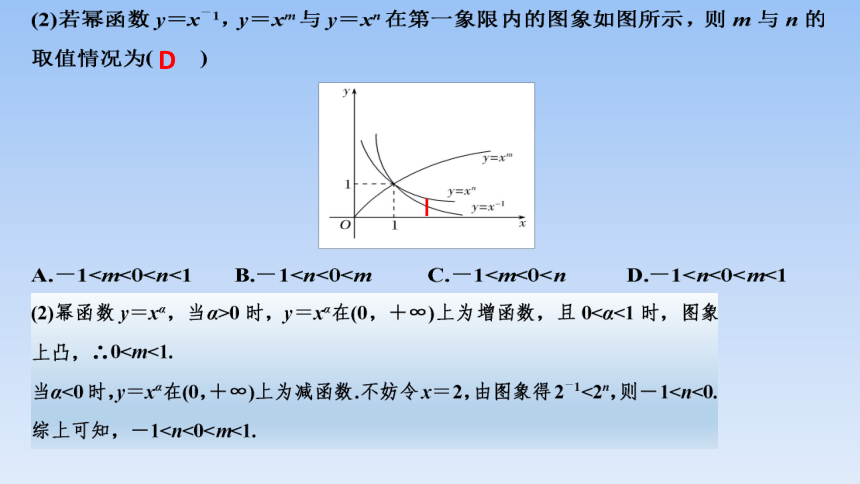
A
D
考点二:二次函数的解析式
x2-4x+3
考点二:二次函数的解析式
x2-4x+3
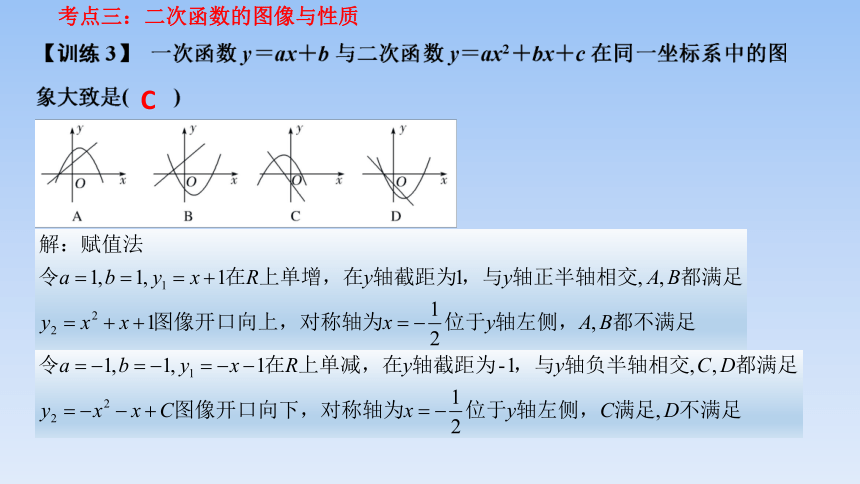
考点三:二次函数的图像与性质
C
考点四:二次函数的性质-单调性
A
考点四:二次函数的性质-恒成立问题
A
B
B
B
D
1
[0,4]
二次函数最值问题的解法:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
解 (1)当a=-2时,
f(x)=x2-4x+3=(x-2)2-1,
由于x∈[-4,6],
∴f(x)在[-4,2]上单调递减,
在[2,6]上单调递增,
∴f(x)的最小值是f(2)=-1,
又f(-4)=35,f(6)=15,
故f(x)的最大值是35.
(2)由于函数f(x)的图象开口向上,
对称轴是x=-a,
所以要使f(x)在[-4,6]上是单调函数,
应有-a≤-4或-a≥6,
即a≤-6或a≥4,
故a的取值范围是(-∞,-6]∪[4,+∞).
A
布置作业
1.复习必修一指数运算与指数函数,完成复习大书23-24页知识梳理和
诊断自测1-6,拍照发云校家课前导学里
2.完成复习大书24-25页例1(1)例2(2),例3-1,例3-2(1)(2),
例3-3(2),拍照发云校家课后作业里
2.4幂函数与二次函数第2课时
考点一:幂函数的图像与性质
A
D
考点二:二次函数的解析式
x2-4x+3
考点二:二次函数的解析式
x2-4x+3
考点三:二次函数的图像与性质
C
考点四:二次函数的性质-单调性
A
考点四:二次函数的性质-恒成立问题
A
B
B
B
D
1
[0,4]
二次函数最值问题的解法:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
解 (1)当a=-2时,
f(x)=x2-4x+3=(x-2)2-1,
由于x∈[-4,6],
∴f(x)在[-4,2]上单调递减,
在[2,6]上单调递增,
∴f(x)的最小值是f(2)=-1,
又f(-4)=35,f(6)=15,
故f(x)的最大值是35.
(2)由于函数f(x)的图象开口向上,
对称轴是x=-a,
所以要使f(x)在[-4,6]上是单调函数,
应有-a≤-4或-a≥6,
即a≤-6或a≥4,
故a的取值范围是(-∞,-6]∪[4,+∞).
A
布置作业
1.复习必修一指数运算与指数函数,完成复习大书23-24页知识梳理和
诊断自测1-6,拍照发云校家课前导学里
2.完成复习大书24-25页例1(1)例2(2),例3-1,例3-2(1)(2),
例3-3(2),拍照发云校家课后作业里
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
