高中数学人教A版必修第一册教案 3.4函数的应用 教案1(含答案)
文档属性
| 名称 | 高中数学人教A版必修第一册教案 3.4函数的应用 教案1(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-05 00:00:00 | ||
图片预览

文档简介
§3.4函数的应用
1教学目标
结合具体的现实问题情境,合理选择已经学习过的正比例函数,反比例函数,一次函数,二次函数,幂函数以及分段函数等函数模型,解决简单的实际问题。
2教学过程
一.常见的数学模型有哪些
(1)一次函数模型:_______________________
(2 )反比例函数模型:_______________________
(3)二次函数模型:_________________________
(4)幂函数模型:_________________________
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
二.练习
1.某自行车存车处在某一天总共存放车辆4000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆。若该天普通自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4000)
B.y=0.5x(0≤x≤4000)
C.y=-0.1x+1200(0≤x≤4000)
D.y=0.1x+1200(0≤x≤4000)
2.某物体一天内的温度T是时间t的函数T(t)=t3-3t+60,时间单位是h,温度单位为℃,t=0时表示中午12:00,则上午8:00时的温度为_______℃.
三.典例分析
例1.依法纳税是每个公民尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定。
计算公式为:个税税额=应纳税所得额×税率一速算扣除数。①
立纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除一专项附加扣除一依法确定的其他扣除。②
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见表
假定小王缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,全年综合所得收入额为x (单位:元) ,那么他全年应缴纳综合所得个税为y(单位:元)
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得为24960元,那么他全年应缴纳多少综合所得个税
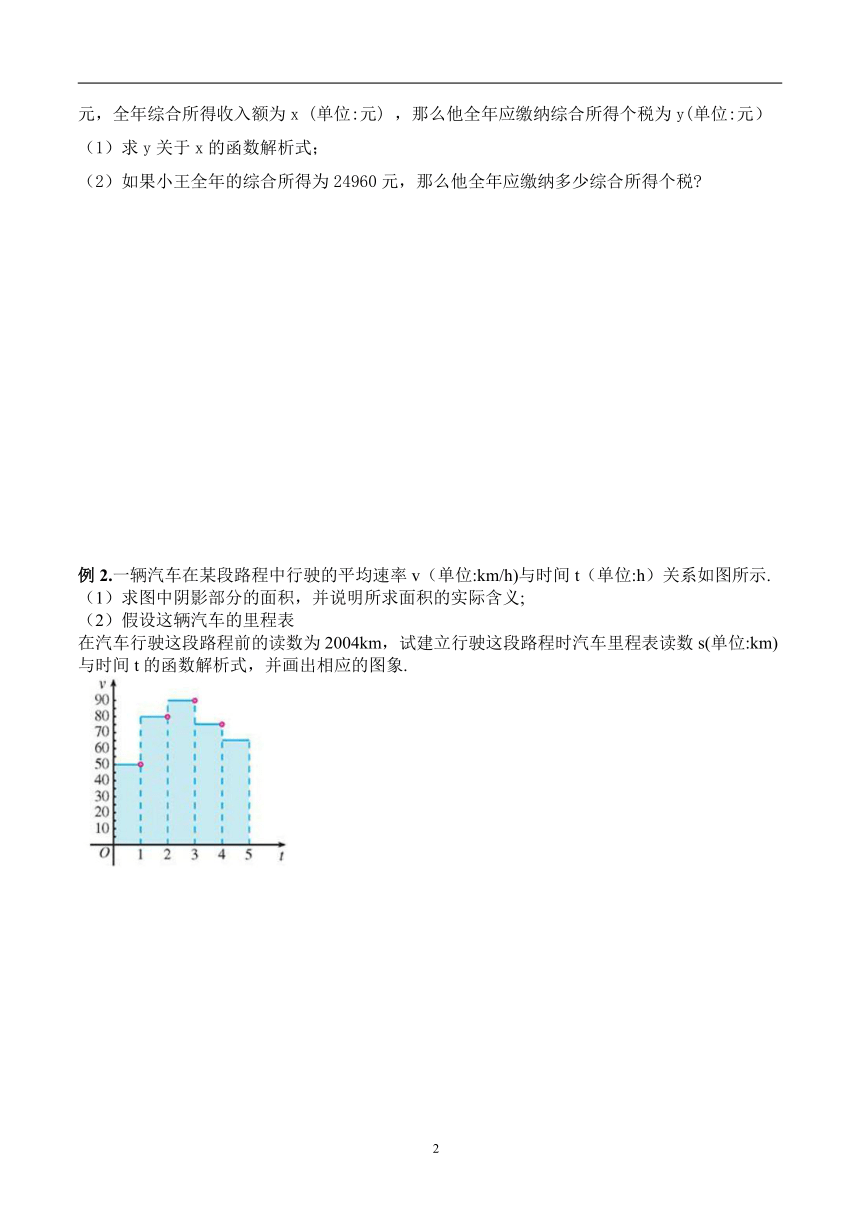
例2.一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表
在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数s(单位:km)
与时间t的函数解析式,并画出相应的图象.
例3.某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000 C.4 000套 D.5 000套
例4某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱.价格每提高1元,平均每天少销售3箱.
①求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
②求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
③当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
例5.北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。该商品原来每件售价为25元,年销售8万件.
(1)据市 场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入(x2-600)万作为技改费用,投入50万元作为固定宣传费用,投入万元作为浮动宣传费用.
试问:当该商品改革后的销 售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
【巩固练习】
A层次课本95页1--3题。
B层次
1、商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
2.某商店进货单价为45元,若按50元一个销售,能卖出50个;若销售单价每涨1元,其销售量就减少2个,为了获得最大利润,此商品的最佳售价应为每个________元.
3.某人从A地出发,开汽车以80千米/小时的速度经2小时到达B地,在B地停留2小时,则汽车离开A地的距离y(单位:千米)是时间t(单位:小时)的函数,该函数的解析式是________.
C层次
4.某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,t小时内供水总量为120 吨(0≤t≤24).
①从供水开始到第几小时时,蓄水池中的存水量最少 最少存水量是多少吨
②若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象.
4
3
1教学目标
结合具体的现实问题情境,合理选择已经学习过的正比例函数,反比例函数,一次函数,二次函数,幂函数以及分段函数等函数模型,解决简单的实际问题。
2教学过程
一.常见的数学模型有哪些
(1)一次函数模型:_______________________
(2 )反比例函数模型:_______________________
(3)二次函数模型:_________________________
(4)幂函数模型:_________________________
(5)分段函数模型:这个模型实则是以上两种或多种模型的综合,因此应用也十分广泛.
二.练习
1.某自行车存车处在某一天总共存放车辆4000辆次,存车费为:电动自行车0.3元/辆,普通自行车0.2元/辆。若该天普通自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4000)
B.y=0.5x(0≤x≤4000)
C.y=-0.1x+1200(0≤x≤4000)
D.y=0.1x+1200(0≤x≤4000)
2.某物体一天内的温度T是时间t的函数T(t)=t3-3t+60,时间单位是h,温度单位为℃,t=0时表示中午12:00,则上午8:00时的温度为_______℃.
三.典例分析
例1.依法纳税是每个公民尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定。
计算公式为:个税税额=应纳税所得额×税率一速算扣除数。①
立纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除一专项附加扣除一依法确定的其他扣除。②
其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见表
假定小王缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,全年综合所得收入额为x (单位:元) ,那么他全年应缴纳综合所得个税为y(单位:元)
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得为24960元,那么他全年应缴纳多少综合所得个税
例2.一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)关系如图所示.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;
(2)假设这辆汽车的里程表
在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数s(单位:km)
与时间t的函数解析式,并画出相应的图象.
例3.某厂日生产文具盒的总成本y(元)与日产量x(套)之间的关系为y=6x+30 000.而出厂价格为每套12元,要使该厂不亏本,至少日生产文具盒( )
A.2 000套 B.3 000 C.4 000套 D.5 000套
例4某水果批发商销售每箱进价为40元的苹果,假设每箱售价不得低于50元且不得高于55元.市场调查发现,若每箱以50元的价格销售,平均每天销售90箱.价格每提高1元,平均每天少销售3箱.
①求平均每天的销售量y(箱)与销售单价x(元/箱)之间的函数关系式;
②求该批发商平均每天的销售利润w(元)与销售单价x(元/箱)之间的函数关系式;
③当每箱苹果的售价为多少元时,可以获得最大利润 最大利润是多少
例5.北京、张家港2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估。该商品原来每件售价为25元,年销售8万件.
(1)据市 场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入(x2-600)万作为技改费用,投入50万元作为固定宣传费用,投入万元作为浮动宣传费用.
试问:当该商品改革后的销 售量a至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
【巩固练习】
A层次课本95页1--3题。
B层次
1、商店出售茶壶和茶杯,茶壶定价为每个20元,茶杯每个5元,该商店推出两种优惠办法:
①买一个茶壶赠一个茶杯;
②按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯x(个),付款y(元),试分别建立两种优惠办法中y与x之间的函数解析式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠
2.某商店进货单价为45元,若按50元一个销售,能卖出50个;若销售单价每涨1元,其销售量就减少2个,为了获得最大利润,此商品的最佳售价应为每个________元.
3.某人从A地出发,开汽车以80千米/小时的速度经2小时到达B地,在B地停留2小时,则汽车离开A地的距离y(单位:千米)是时间t(单位:小时)的函数,该函数的解析式是________.
C层次
4.某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,t小时内供水总量为120 吨(0≤t≤24).
①从供水开始到第几小时时,蓄水池中的存水量最少 最少存水量是多少吨
②若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象.
4
3
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
