2022—2023学年沪科版数学八年级上册14.2 三角形全等的判定(3)课件 (共17张PPT)
文档属性
| 名称 | 2022—2023学年沪科版数学八年级上册14.2 三角形全等的判定(3)课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 21:12:11 | ||
图片预览






文档简介
(共17张PPT)
14.2 三角形全等的判定
三边分别相等的两个三角形
学习目标
准备好了吗?一起去探索吧!
1.理解并掌握判定两个三角形全等“边边边”判定定理.
2.在探究“边边边”判定定理的过程中,能进行有条理的思考.
3.通过学习以上内容,培养严谨的分析能力,体会几何学的应用价值.
4.通过探究对给定的三边的长度来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力.
三
角
形
全
等
的
判
定
-
SSS
到目前为止,可以作为判定两个三角形全等的方法有几种?
回顾
定义
能够完全重合的两个三角形全等.
边角边(SAS)
两边及其夹角分别相等的两个三角形全等.
角边角(ASA)
两角及其夹边分别相等的两个三角形全等.
我们继续探究三角形全等的判定方法!
情境引入
日常生活中,常会看到应用三角形稳定性的例子,如下三种情况.
为什么说三角形具有稳定性呢?
操作
拼出的三角形的大小和形状都是一样的!
7 cm
6 cm
5 cm
7 cm
6 cm
5 cm
跟同组小伙伴拼出的三角形比一比,你发现了什么?
请你用如下三根小棒拼一个三角形.
操作
已知:△ABC.
求作:△A'B'C',使A'B'=AB,B'C'=BC ,使C'A'=CA.
作法:
(1)作线段B′C′=BC;
(2)分别以点B′,C′为圆心,线段AB、AC长为半径画弧,两弧相交于点A′;
(3)连接A′B′,A′C′得△A′B′C′.
A
B
C
B′
M
C′
A′
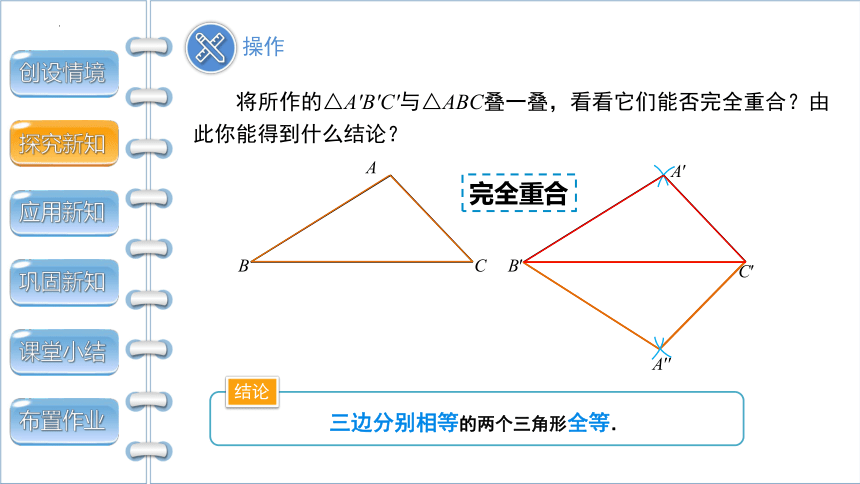
操作
A
B
C
B′
C′
A′
完全重合
A′′
结论
三边分别相等的两个三角形全等.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
归纳
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
几何语言:
如图,在△ABC与△A'B'C'中:
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
AC=A'C',
BC=B'C',
B′
A′
C′
B
A
C
想一想
现在你能解释三角形的稳定性了吗?
根据三角形全等的判定定理——边边边,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.
请你再照样举一些生活中的例子!
典型例题
例 已知:如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:AB∥DE,AC∥DF.
E
D
F
B
A
C
分析:要证明线平行,可通过角相等
结合平行线的判定定理证明;
证明角相等可通过三角形全等得到.
“△ABC和△DEF”
已知:AB=DE,AC=DF,
由“BE=CF”得“BE+EC=CF+EC”,
即BC=EF.
我们在找相等的边时,注意隐含的条件相等的边——相等的边之间的差或和.
典型例题
例 已知:如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:AB∥DE,AC∥DF.
E
D
F
B
A
C
证明:∵BE=CF,(已知)
∴ BE+EC=CF+EC,(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∴ △ABC≌△DEF.(SSS)
∴ ∠B=∠DEF,∠ACB=∠F.(全等三角形的对应角相等)
∴ AB∥DE,AC∥DF.(同位角相等,两直线平行)
抢答
随堂练习
1.在下图中找出全等三角形.
(1)和(10)
(2)和(6)
(3)和(5)
(4)和(8)
(7)和(9)
边边边
边角边
角边角
抢答
随堂练习
2.如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
我们在找相等的边时,注意隐含的条件相等的边——公共边.
证明:
∵D是BC的中点,
∴BD=CD.
在△ABD和≌△ACD中,
AB=AC,(已知)
BD=CD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(SSS).
抢答
随堂练习
3.已知:如图,在△ABC中,AB=AC.点D,E在BC上,且AD=AE,
BE=CD.求证:△ABD≌△ACE.
E
D
B
A
C
证明:∵BE=CD,(已知)
∴ BE–DE=CD–DE,(等式的性质)
即BD=CE.
在△ABD和△ACE中,
∴ △ABD≌△ACE.(SSS)
三
角
形
全
等
的
判
定
-
SSS
三角形全等的判定-SSS:
三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
几何语言:
如图,在△ABC与△A'B'C'中:
∴△ABC≌△A'B'C'(SSS).
B′
A′
C′
B
A
C
AB=A'B',
BC=B'C',
AC=A'C',
找相等的边:
相等的边之间的差或和
公共边
教科书第111页习题14.2
第11题
再见
14.2 三角形全等的判定
三边分别相等的两个三角形
学习目标
准备好了吗?一起去探索吧!
1.理解并掌握判定两个三角形全等“边边边”判定定理.
2.在探究“边边边”判定定理的过程中,能进行有条理的思考.
3.通过学习以上内容,培养严谨的分析能力,体会几何学的应用价值.
4.通过探究对给定的三边的长度来确定三角形的形状和大小是否唯一这一过程,培养学生分析问题、解决问题的能力.
三
角
形
全
等
的
判
定
-
SSS
到目前为止,可以作为判定两个三角形全等的方法有几种?
回顾
定义
能够完全重合的两个三角形全等.
边角边(SAS)
两边及其夹角分别相等的两个三角形全等.
角边角(ASA)
两角及其夹边分别相等的两个三角形全等.
我们继续探究三角形全等的判定方法!
情境引入
日常生活中,常会看到应用三角形稳定性的例子,如下三种情况.
为什么说三角形具有稳定性呢?
操作
拼出的三角形的大小和形状都是一样的!
7 cm
6 cm
5 cm
7 cm
6 cm
5 cm
跟同组小伙伴拼出的三角形比一比,你发现了什么?
请你用如下三根小棒拼一个三角形.
操作
已知:△ABC.
求作:△A'B'C',使A'B'=AB,B'C'=BC ,使C'A'=CA.
作法:
(1)作线段B′C′=BC;
(2)分别以点B′,C′为圆心,线段AB、AC长为半径画弧,两弧相交于点A′;
(3)连接A′B′,A′C′得△A′B′C′.
A
B
C
B′
M
C′
A′
操作
A
B
C
B′
C′
A′
完全重合
A′′
结论
三边分别相等的两个三角形全等.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合?由此你能得到什么结论?
归纳
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
几何语言:
如图,在△ABC与△A'B'C'中:
∴△ABC≌△A'B'C'(SSS).
AB=A'B',
AC=A'C',
BC=B'C',
B′
A′
C′
B
A
C
想一想
现在你能解释三角形的稳定性了吗?
根据三角形全等的判定定理——边边边,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.
请你再照样举一些生活中的例子!
典型例题
例 已知:如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:AB∥DE,AC∥DF.
E
D
F
B
A
C
分析:要证明线平行,可通过角相等
结合平行线的判定定理证明;
证明角相等可通过三角形全等得到.
“△ABC和△DEF”
已知:AB=DE,AC=DF,
由“BE=CF”得“BE+EC=CF+EC”,
即BC=EF.
我们在找相等的边时,注意隐含的条件相等的边——相等的边之间的差或和.
典型例题
例 已知:如图,点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.
求证:AB∥DE,AC∥DF.
E
D
F
B
A
C
证明:∵BE=CF,(已知)
∴ BE+EC=CF+EC,(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∴ △ABC≌△DEF.(SSS)
∴ ∠B=∠DEF,∠ACB=∠F.(全等三角形的对应角相等)
∴ AB∥DE,AC∥DF.(同位角相等,两直线平行)
抢答
随堂练习
1.在下图中找出全等三角形.
(1)和(10)
(2)和(6)
(3)和(5)
(4)和(8)
(7)和(9)
边边边
边角边
角边角
抢答
随堂练习
2.如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
我们在找相等的边时,注意隐含的条件相等的边——公共边.
证明:
∵D是BC的中点,
∴BD=CD.
在△ABD和≌△ACD中,
AB=AC,(已知)
BD=CD,(已证)
AD=AD,(公共边)
∴ △ABD≌△ACD(SSS).
抢答
随堂练习
3.已知:如图,在△ABC中,AB=AC.点D,E在BC上,且AD=AE,
BE=CD.求证:△ABD≌△ACE.
E
D
B
A
C
证明:∵BE=CD,(已知)
∴ BE–DE=CD–DE,(等式的性质)
即BD=CE.
在△ABD和△ACE中,
∴ △ABD≌△ACE.(SSS)
三
角
形
全
等
的
判
定
-
SSS
三角形全等的判定-SSS:
三边分别相等的两个三角形全等.
简记为“边边边”或“SSS”.
几何语言:
如图,在△ABC与△A'B'C'中:
∴△ABC≌△A'B'C'(SSS).
B′
A′
C′
B
A
C
AB=A'B',
BC=B'C',
AC=A'C',
找相等的边:
相等的边之间的差或和
公共边
教科书第111页习题14.2
第11题
再见
