高中数学人教A版必修第一册课件4.2 指数函数 课件(共15张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件4.2 指数函数 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 39.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 10:58:37 | ||
图片预览





文档简介
(共15张PPT)
第4章 指数函数与对数函数
4.2 指数函数
人教A版2019高中数学必修第一册
什么是指数函数?
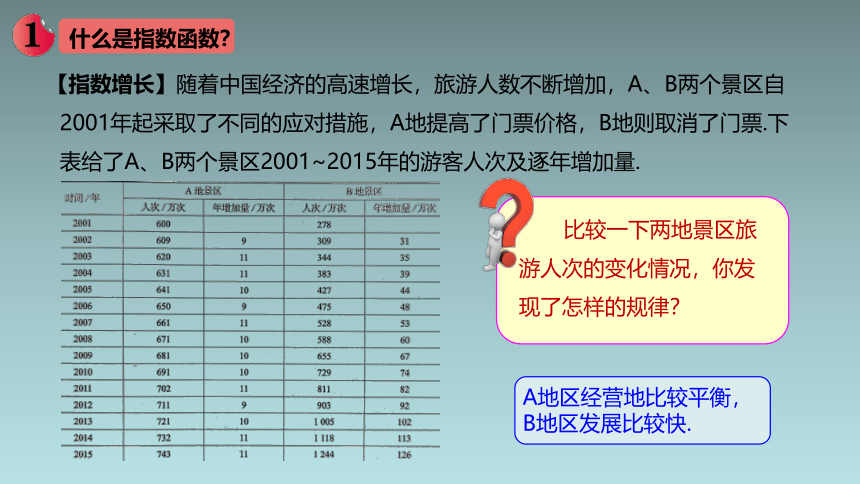
【指数增长】随着中国经济的高速增长,旅游人数不断增加,A、B两个景区自
2001年起采取了不同的应对措施,A地提高了门票价格,B地则取消了门票.下
表给了A、B两个景区2001~2015年的游客人次及逐年增加量.
比较一下两地景区旅游人次的变化情况,你发现了怎样的规律?
A地区经营地比较平衡,B地区发展比较快.
什么是指数函数?
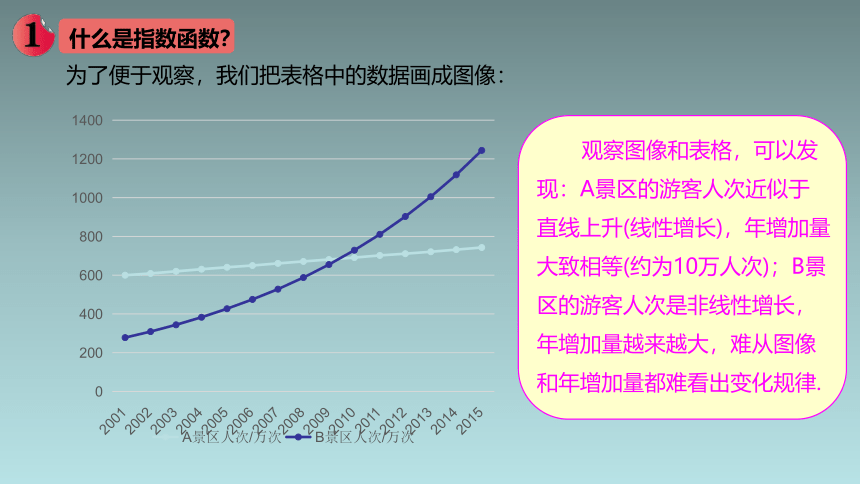
为了便于观察,我们把表格中的数据画成图像:
观察图像和表格,可以发现:A景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为10万人次);B景区的游客人次是非线性增长,年增加量越来越大,难从图像和年增加量都难看出变化规律.
什么是指数函数?
【探究】我们知道,年增加量是对相邻两年的游客人次做减法得到的.那么能否通过
对B景区每年的游客人次做其他运算来发现规律呢?
增加量=变后量-变前量
【尝试】从2002年起,将B景区每年的游客人次除以上一年的游客人次,可以得到
2002年游客人次
2001年游客人次
=
2003年游客人次
2002年游客人次
=
2015年游客人次
2014年游客人次
=
增长率=
增加量
变前量
【结论】结果表明,B景区的游客人次的年增长率都约为1.11-1=0.11,是一个常数.
什么是指数函数?
【总结】像这样,增长率为常数的变化方式,称为指数增长.因此,B景区的游客
人数近似于指数增长.即从2011年起,每一年的游客人次都是上一年的
1.1倍左右,增长量越来越多.
t年后,B景区游客人次是2011年的1.11t倍.即t年后B景区的游客人次:
容易看出这是一个函数,其中指数t是自变量.
【指数衰减】南极冬季的冰架面积大约为1880万平方千米,假设冰川每年融化0.1%,
那么n年后南极的冰川的剩余量W为:
什么是指数函数?
【定义】如果用字母 代替上述两个问题中的底数1.11和0.999,那么函数
一般地,函数 叫做指数函数.
其中 是自变量,定义域是R.
和 就都可以表示为 的形式,
其中, 是自变量,底数 是一个大于0且不等于1的常量.
所以它是指数函数.
指数函数的结构特征.
【1】 解析式中 的系数为1
【2】 底数 是常数,满足
【3】 自变量 是指数,且
因此,指数函数的定义只是一个形式定义.判断一个函数是不是指数函数关键是看这个函数的解析式变形整理之后是不是具备以上三个特征.
例如, 等都是指数函数,这是因为
其中, 称为指数型函数,
称为正整数指数函数.
指数函数的结构特征.
【问题】 指数函数 中为什么规定 ?
【答】 ①若 ,则当 时, ;当 时, 无意义.
②若 ,则对于 的某些数值,可以 无意义.如 ,这
时对于 等情况在实数范围内函数值不存在.
②若 ,则对于任意 , ,是一个常量,没有研究
的必要.为了避免上述情况的发生,所以规定 ,这样
规定之后,对于任意的实数 , 都有意义且 .
指数函数的图像和性质
【二】指数函数的性质:在同一坐标系中作出底数不同的指数函数图像.
-3 -2 -1 1 2 3
1
一般地,指数函数的图像和性质如下表所示:
(1)过定点(0,1)
(2)减函数
(3)增函数
指数函数的图像和性质
【1】指数函数既不是奇函数也不是偶函数
【2】指数函数在y轴右侧的图像,底数越大
图像越高.(底大图高)
-3 -2 -1 1 2 3
1
【3】①当
②当
③当
④当
【4】指数函数图像下端与 轴无限接近,
但永不相交.
【5】指数函数都是下凸的函数.
指数函数的应用
【例题】比较下列各题中两个值的大小.
【解】(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(2)函数 是减函数,且 ,则
(3)
【1】求下列函数的定义域和值域.
【解】(1)
(2)
【2】不论 为何值,函数 的图像一定经过点P,
则点P的坐标是多少?
【解】(方法一)当
所以函数经过定点(2,2)
(方法二)因为指数函数 经过定点(0,1),
所以当 ,此时
所以函数经过定点(2,2)
【3】求出函数 的单调区间.
【解】设
易知 在 上是增函数,在 上是减函数
当 时, 在R上单调递增,
所以 在 上是增函数,在 上是减函数
THANKS
“
”
第4章 指数函数与对数函数
4.2 指数函数
人教A版2019高中数学必修第一册
什么是指数函数?
【指数增长】随着中国经济的高速增长,旅游人数不断增加,A、B两个景区自
2001年起采取了不同的应对措施,A地提高了门票价格,B地则取消了门票.下
表给了A、B两个景区2001~2015年的游客人次及逐年增加量.
比较一下两地景区旅游人次的变化情况,你发现了怎样的规律?
A地区经营地比较平衡,B地区发展比较快.
什么是指数函数?
为了便于观察,我们把表格中的数据画成图像:
观察图像和表格,可以发现:A景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为10万人次);B景区的游客人次是非线性增长,年增加量越来越大,难从图像和年增加量都难看出变化规律.
什么是指数函数?
【探究】我们知道,年增加量是对相邻两年的游客人次做减法得到的.那么能否通过
对B景区每年的游客人次做其他运算来发现规律呢?
增加量=变后量-变前量
【尝试】从2002年起,将B景区每年的游客人次除以上一年的游客人次,可以得到
2002年游客人次
2001年游客人次
=
2003年游客人次
2002年游客人次
=
2015年游客人次
2014年游客人次
=
增长率=
增加量
变前量
【结论】结果表明,B景区的游客人次的年增长率都约为1.11-1=0.11,是一个常数.
什么是指数函数?
【总结】像这样,增长率为常数的变化方式,称为指数增长.因此,B景区的游客
人数近似于指数增长.即从2011年起,每一年的游客人次都是上一年的
1.1倍左右,增长量越来越多.
t年后,B景区游客人次是2011年的1.11t倍.即t年后B景区的游客人次:
容易看出这是一个函数,其中指数t是自变量.
【指数衰减】南极冬季的冰架面积大约为1880万平方千米,假设冰川每年融化0.1%,
那么n年后南极的冰川的剩余量W为:
什么是指数函数?
【定义】如果用字母 代替上述两个问题中的底数1.11和0.999,那么函数
一般地,函数 叫做指数函数.
其中 是自变量,定义域是R.
和 就都可以表示为 的形式,
其中, 是自变量,底数 是一个大于0且不等于1的常量.
所以它是指数函数.
指数函数的结构特征.
【1】 解析式中 的系数为1
【2】 底数 是常数,满足
【3】 自变量 是指数,且
因此,指数函数的定义只是一个形式定义.判断一个函数是不是指数函数关键是看这个函数的解析式变形整理之后是不是具备以上三个特征.
例如, 等都是指数函数,这是因为
其中, 称为指数型函数,
称为正整数指数函数.
指数函数的结构特征.
【问题】 指数函数 中为什么规定 ?
【答】 ①若 ,则当 时, ;当 时, 无意义.
②若 ,则对于 的某些数值,可以 无意义.如 ,这
时对于 等情况在实数范围内函数值不存在.
②若 ,则对于任意 , ,是一个常量,没有研究
的必要.为了避免上述情况的发生,所以规定 ,这样
规定之后,对于任意的实数 , 都有意义且 .
指数函数的图像和性质
【二】指数函数的性质:在同一坐标系中作出底数不同的指数函数图像.
-3 -2 -1 1 2 3
1
一般地,指数函数的图像和性质如下表所示:
(1)过定点(0,1)
(2)减函数
(3)增函数
指数函数的图像和性质
【1】指数函数既不是奇函数也不是偶函数
【2】指数函数在y轴右侧的图像,底数越大
图像越高.(底大图高)
-3 -2 -1 1 2 3
1
【3】①当
②当
③当
④当
【4】指数函数图像下端与 轴无限接近,
但永不相交.
【5】指数函数都是下凸的函数.
指数函数的应用
【例题】比较下列各题中两个值的大小.
【解】(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(2)函数 是减函数,且 ,则
(3)
【1】求下列函数的定义域和值域.
【解】(1)
(2)
【2】不论 为何值,函数 的图像一定经过点P,
则点P的坐标是多少?
【解】(方法一)当
所以函数经过定点(2,2)
(方法二)因为指数函数 经过定点(0,1),
所以当 ,此时
所以函数经过定点(2,2)
【3】求出函数 的单调区间.
【解】设
易知 在 上是增函数,在 上是减函数
当 时, 在R上单调递增,
所以 在 上是增函数,在 上是减函数
THANKS
“
”
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
