人教版数学七年级上册 第一章有理数小结 课件(共31张PPT)
文档属性
| 名称 | 人教版数学七年级上册 第一章有理数小结 课件(共31张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 10:40:50 | ||
图片预览










文档简介
(共31张PPT)
第一章 有理数总复习
1.负数
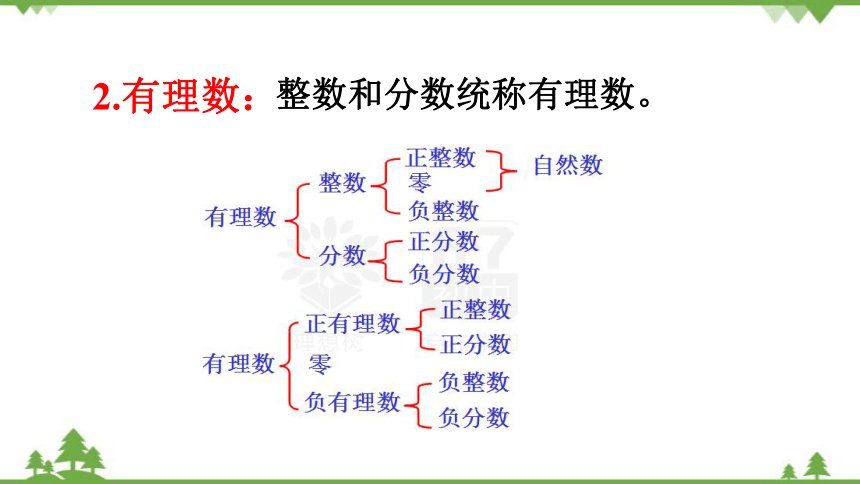
2.有理数
3.数轴
4.互为相反数、互为倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数
一、有理数的基本概念
二、有理数的运算
加、减、乘、除、乘方运算
2.有理数:
整数和分数统称有理数。
3.数 轴
4.相反数
5.倒 数
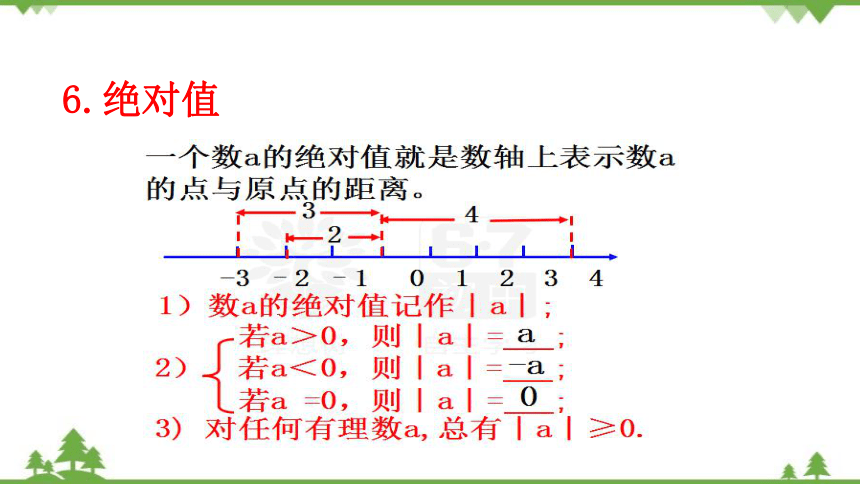
6.绝对值
7.有理数大小的比较
1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.
1)有理数加法法则
① 同号两数相加,取相同的符号,并把绝对值相加;
② 绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两数相加得0;
③ 一个数同0相加,仍得这个数。
2)有理数减法法则
减去一个数,等于加上这个数的相反数.
即 a-b=a+(-b)
例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。
解:①2-(-7)=2+7=9
(或︱-7-2︱=︱-9︱=9)
②-1-(-3)=-1+3=2
3)有理数的乘法法则
4)有理数除法法则
①除以一个数等于乘上这个数的倒数;
即
a÷b=a× (b≠0)
② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都得0.
2.运算顺序
1)有括号,先算括号里面的;
2)先算乘方,再算乘除,
最后算加减;
3)对只含乘除,或只含加减的
运算,应从左往右运算。
5)有理数的乘方
8.科学记数法、近似数
1. 把一个大于10的数记成a×10n
的形式,其中a是整数数位只有一位
的数,这种记数法叫做科学记数法 .
判断:
①带“-”号的数都是负数
②-a一定是负数
③不存在既不是正数,也不是负数的数
④0℃表示没有温度
增加-20%,实际的意思是 .
甲比乙大-3表示的意思是 .
正负数的概念
数轴的概念 ★★选择题:
(1)在数轴上,原点及原点左边所表示的数( )
A整数 B负数 C非负数 D非正数
(2)下列语句中正确的是( ) A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
(5)在数轴上点A表示-4,如果把原点O向负方向移
动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
D
D
C
1、 -(-8)的相反数是 ;
- [+(-6)]=_____,a的相反数是 ;
-8 的相反数的倒数是______________ ;
2、若a和b是互为相反数,则a+b=( )
A. –2a B .2b C. 0 D. 任意有理数
3、(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)如果-x=9,那么x=______.
4、用-a表示的数一定是( )
A .负数 B. 正数
C .正数或负数 D.正数或负数或0
5、一个数的相反数是最小的正整数,那么这个数是( )
A .–1 B. 1 C .±1 D. 0
D
A
1、-|-5|= ; 绝对值等于4的数是__________。
2、绝对值等于其相反数的数一定是( ) A.负数 B.正数
C.负数或零 D.正数或零
3、★ 若 ,则x=______;
若 则 x=_______;
4、已知a、b都是有理数,且|a|=a,|b|=-b则ab是( )
A.负数 B.正数 C.负数或零 D.非负数
绝对值训练
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上
表示a的点在表示b的点左侧,则b的值为 .
0,±1
零和正数
-1,-2,-3
5
绝对值训练
1、若(x-1)2+|y+4|=0,则3x+5y=______
2、若|a-3|+ |3a-4b|=0,则-2a+8b=____
绝对值训练
3、已知|x|=3,|y|=2,且x4、计算
1、用科学记数数表示:
①1305000000= ;
②-1020= .
2、水星和太阳的平均距离约为57900000
km用科学记数法表示为
3、 120万用科学记数法应写成 ;
2.4万的原数是 .
4、 近似数3.5万精确到 位
5、 近似数0.4062精确到 位
科学计数法及近似数
例:下列由四舍五入得到的近似数,各精确到哪一位?
(1)43.8(2)0.03086(3)2.4万
(4)6×104 (5)6.0×104
(1)43.8精确到十分位.
(2)0.03086精确到十万分位,
(3)2.4万精确到千位,
(4) 6×104 精确到万位,
(5) 6.0×104 精确到千位,
下面的解题过程是否正确?如果有错误请加以订正。
改正:
有理数的运算
专题训练
已知a、b互为相反数,c,d互为倒数,m是绝对值最小的数,求代数式
的值
非负数性质的应用
1、若a>0,b<0,且|a|<|b|,则a+b___0
特殊值法
2、若x<0,y>0,且|x|<|y|,则x+y__0
1、已知有理数a、b、c在数轴上的位置如图,
化简|a|-|a+b|+|c-a|+|b+c||
拓展延伸
第一章 有理数总复习
1.负数
2.有理数
3.数轴
4.互为相反数、互为倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数
一、有理数的基本概念
二、有理数的运算
加、减、乘、除、乘方运算
2.有理数:
整数和分数统称有理数。
3.数 轴
4.相反数
5.倒 数
6.绝对值
7.有理数大小的比较
1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.
1)有理数加法法则
① 同号两数相加,取相同的符号,并把绝对值相加;
② 绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两数相加得0;
③ 一个数同0相加,仍得这个数。
2)有理数减法法则
减去一个数,等于加上这个数的相反数.
即 a-b=a+(-b)
例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。
解:①2-(-7)=2+7=9
(或︱-7-2︱=︱-9︱=9)
②-1-(-3)=-1+3=2
3)有理数的乘法法则
4)有理数除法法则
①除以一个数等于乘上这个数的倒数;
即
a÷b=a× (b≠0)
② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都得0.
2.运算顺序
1)有括号,先算括号里面的;
2)先算乘方,再算乘除,
最后算加减;
3)对只含乘除,或只含加减的
运算,应从左往右运算。
5)有理数的乘方
8.科学记数法、近似数
1. 把一个大于10的数记成a×10n
的形式,其中a是整数数位只有一位
的数,这种记数法叫做科学记数法 .
判断:
①带“-”号的数都是负数
②-a一定是负数
③不存在既不是正数,也不是负数的数
④0℃表示没有温度
增加-20%,实际的意思是 .
甲比乙大-3表示的意思是 .
正负数的概念
数轴的概念 ★★选择题:
(1)在数轴上,原点及原点左边所表示的数( )
A整数 B负数 C非负数 D非正数
(2)下列语句中正确的是( ) A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
(5)在数轴上点A表示-4,如果把原点O向负方向移
动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
D
D
C
1、 -(-8)的相反数是 ;
- [+(-6)]=_____,a的相反数是 ;
-8 的相反数的倒数是______________ ;
2、若a和b是互为相反数,则a+b=( )
A. –2a B .2b C. 0 D. 任意有理数
3、(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)如果-x=9,那么x=______.
4、用-a表示的数一定是( )
A .负数 B. 正数
C .正数或负数 D.正数或负数或0
5、一个数的相反数是最小的正整数,那么这个数是( )
A .–1 B. 1 C .±1 D. 0
D
A
1、-|-5|= ; 绝对值等于4的数是__________。
2、绝对值等于其相反数的数一定是( ) A.负数 B.正数
C.负数或零 D.正数或零
3、★ 若 ,则x=______;
若 则 x=_______;
4、已知a、b都是有理数,且|a|=a,|b|=-b则ab是( )
A.负数 B.正数 C.负数或零 D.非负数
绝对值训练
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上
表示a的点在表示b的点左侧,则b的值为 .
0,±1
零和正数
-1,-2,-3
5
绝对值训练
1、若(x-1)2+|y+4|=0,则3x+5y=______
2、若|a-3|+ |3a-4b|=0,则-2a+8b=____
绝对值训练
3、已知|x|=3,|y|=2,且x
1、用科学记数数表示:
①1305000000= ;
②-1020= .
2、水星和太阳的平均距离约为57900000
km用科学记数法表示为
3、 120万用科学记数法应写成 ;
2.4万的原数是 .
4、 近似数3.5万精确到 位
5、 近似数0.4062精确到 位
科学计数法及近似数
例:下列由四舍五入得到的近似数,各精确到哪一位?
(1)43.8(2)0.03086(3)2.4万
(4)6×104 (5)6.0×104
(1)43.8精确到十分位.
(2)0.03086精确到十万分位,
(3)2.4万精确到千位,
(4) 6×104 精确到万位,
(5) 6.0×104 精确到千位,
下面的解题过程是否正确?如果有错误请加以订正。
改正:
有理数的运算
专题训练
已知a、b互为相反数,c,d互为倒数,m是绝对值最小的数,求代数式
的值
非负数性质的应用
1、若a>0,b<0,且|a|<|b|,则a+b___0
特殊值法
2、若x<0,y>0,且|x|<|y|,则x+y__0
1、已知有理数a、b、c在数轴上的位置如图,
化简|a|-|a+b|+|c-a|+|b+c||
拓展延伸
