数学人教A版(2019)必修第一册3.2.2奇偶性(共26张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.2.2奇偶性(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 517.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 11:28:27 | ||
图片预览




文档简介
(共26张PPT)
第一章 统计案例
3.2.2
奇 偶 性
高一数学必修第一册 第三章 函数的概念与性质
学习目标
1.理解函数奇偶性的概念和性质;
2.会判断简单函数的奇偶性;
3.学会运用函数图象理解和研究函数的性质.
4.核心素养:数学抽象、逻辑推理、数学运算.
一、引入新课
现实生活中的“美”的事例
x
y
O
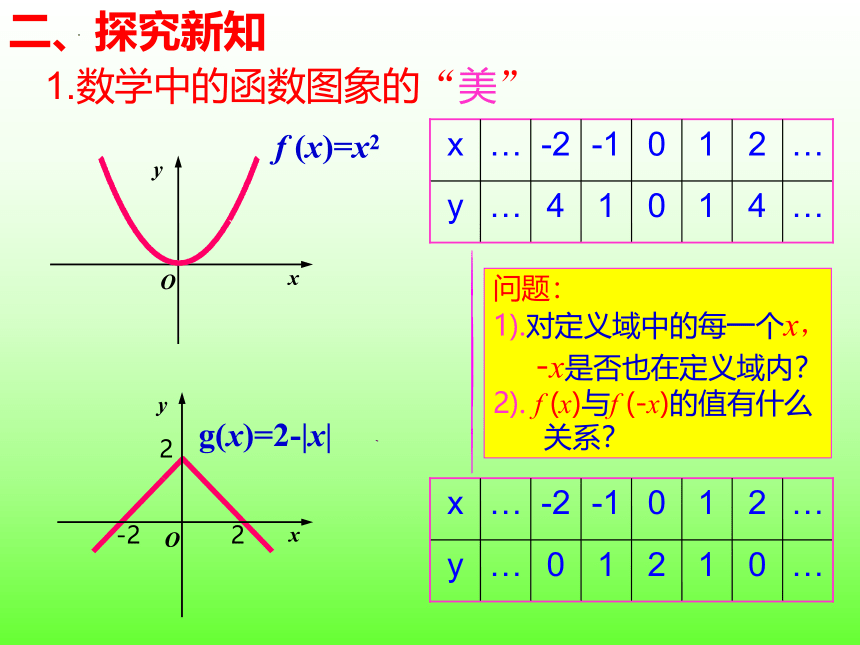
f (x)=x2
g(x)=2-|x|
x … -2 -1 0 1 2 …
y … 4 1 0 1 4 …
x … -2 -1 0 1 2 …
y … 0 1 2 1 0 …
问题:
1).对定义域中的每一个x,
-x是否也在定义域内?
2). f (x)与f (-x)的值有什么
关系?
x
y
O
2
2
-2
二、探究新知
1.数学中的函数图象的“美”
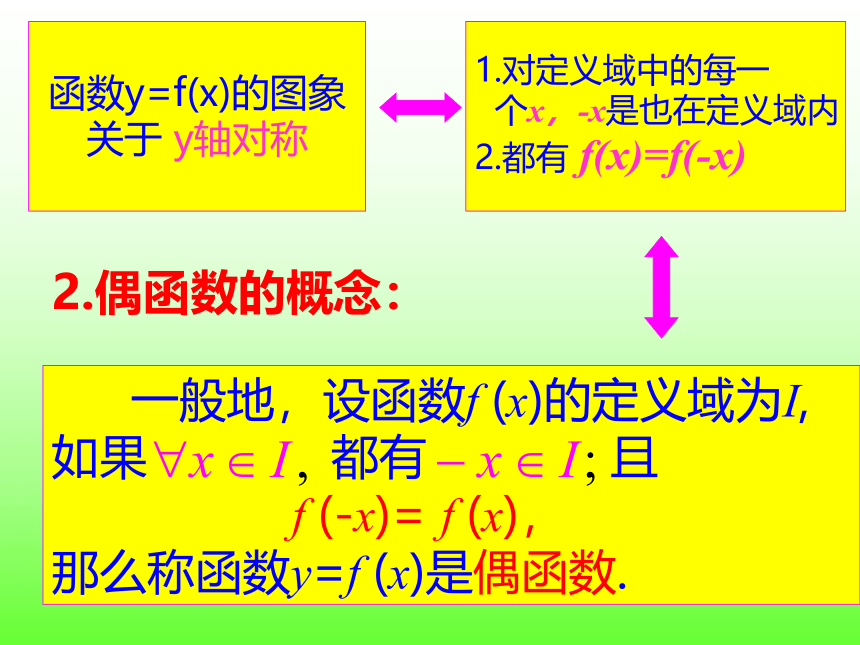
函数y=f(x)的图象
关于 y轴对称
1.对定义域中的每一
个x,-x是也在定义域内
2.都有 f(x)=f(-x)
一般地,设函数f (x)的定义域为I,
如果 都有 且
f (-x)= f (x),
那么称函数y=f (x)是偶函数.
2.偶函数的概念:
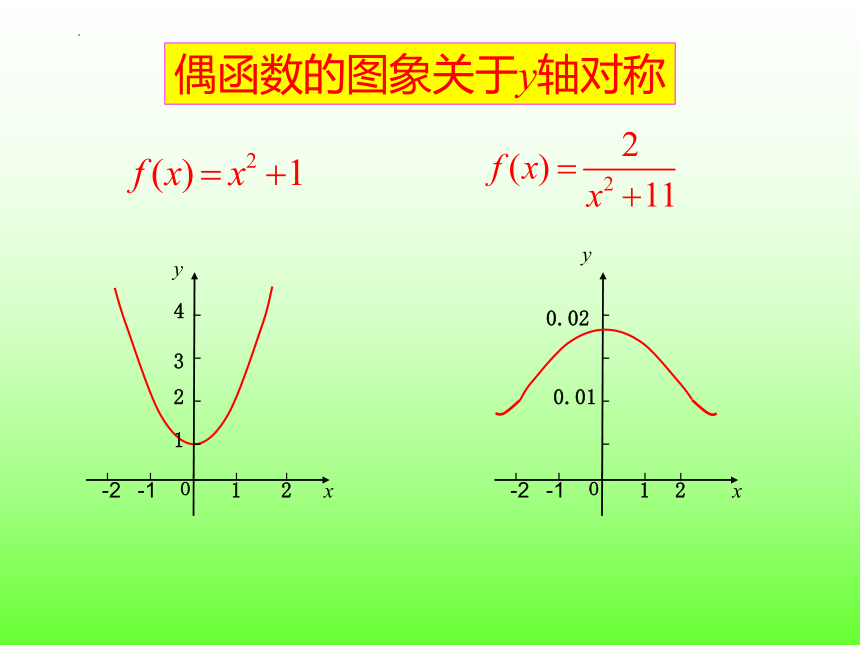
偶函数的图象关于y轴对称
-1
x
y
O
1
2
2
1
3
4
-2
-1
x
y
O
1
2
0.01
0.02
-2
-3
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
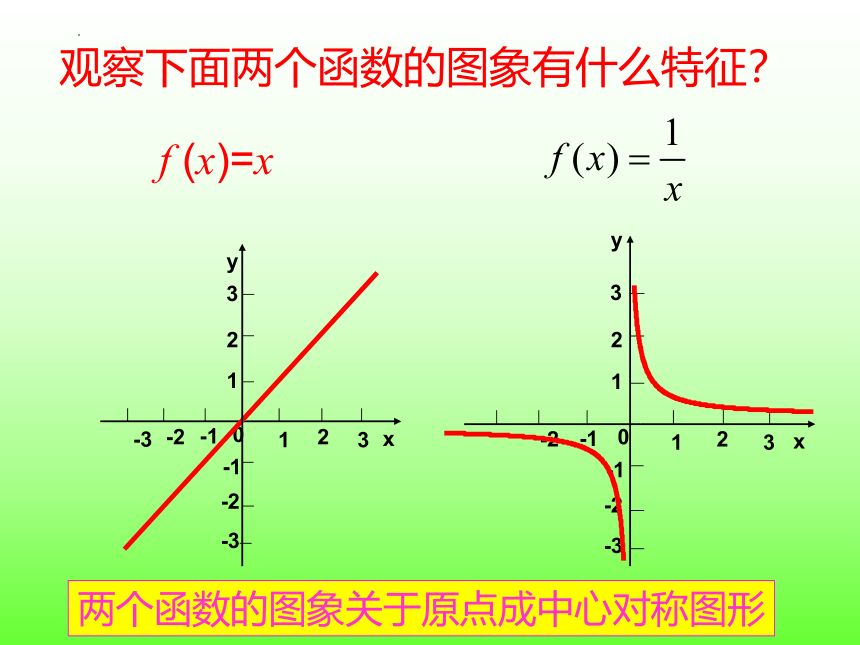
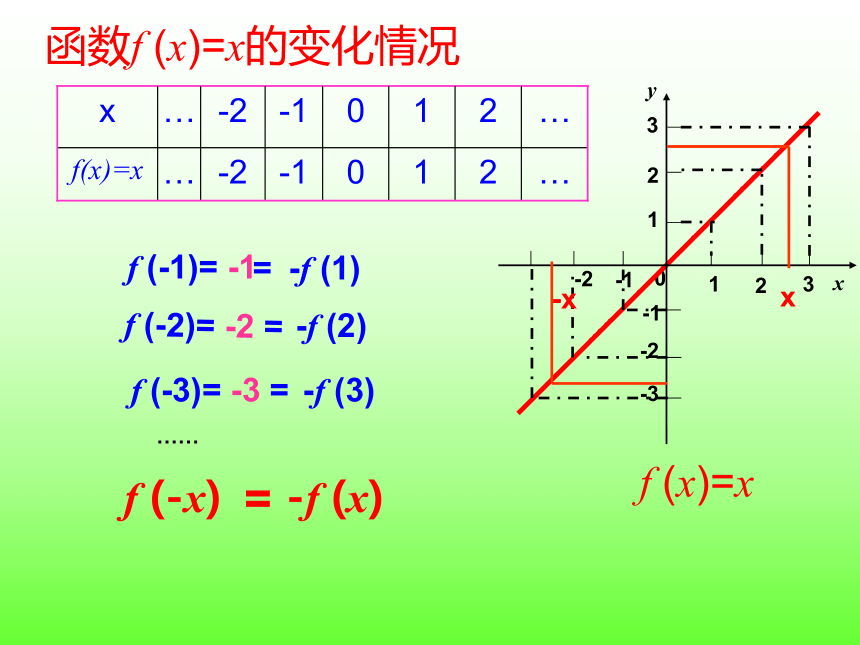
f (x)=x
观察下面两个函数的图象有什么特征?
两个函数的图象关于原点成中心对称图形
f (-3)= -3 =
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
……
f (-x) -f (x)
f (-1)= -1
f (-2)= -2 =
x
-x
-f (1)
=
-f (2)
-f (3)
=
x … -2 -1 0 1 2 …
f(x)=x … -2 -1 0 1 2 …
f (x)=x
函数f (x)=x的变化情况
f (-3)= =-f (3)
f (-1)= -1 =-f (1)
f (-2)= =-f (2)
……
3
2
1
0
-2
-3
x
-1
-1
函数 的变化情况
f (-x) -f (x)
=
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
1
函数y=f(x)的图象
关于 原点对称
1.对定义域中的每一
个x,-x是也在定义域内
2.都有 f(x)= — f(-x)
一般地,设函数f (x)的定义域为I,
如果 都有 且
f (-x)=- f (x),
那么称函数y=f (x)是奇函数.
3.奇函数的概念:
如果一个函数f (x)是奇函数或偶函数,
那么我们就说函数f (x)具有奇偶性.
①定义法:
先看定义域是否关于原点对称,
再看f (-x)与 f (x)的关系.
4.函数的奇偶性:
②图象法:
看图象是否关于原点或y轴对称.
判定函数奇偶性基本方法:
f (x)=0 , x∈R
说明:
1).根据函数的奇偶性
既奇又偶函数
非奇非偶函数
偶函数
奇函数
函数可划分为四类:
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)=0
既是奇函数又是偶函数
非奇非偶函数
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)=3x+1
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)= x2+2x
2).奇、偶函数定义的逆命题也成立,即
若f (x)为奇函数,则f (-x)=-f (x)有成立.
若f (x)为偶函数,则f (-x)=f (x)有成立.
3).奇、偶函数性质:
偶函数的
定义域关于原点对称
图象关于y轴对称
奇函数的
定义域关于原点对称
图象关于原点对称.
如果一个函数是偶函数,则它的图象关于y轴对称.
y=x2
5.偶函数的性质特征
反过来,
如果一个函数的图象关于y轴对称,则这个函数为偶函数.
,
是偶函数吗
问题:
不是
性质:偶函数的定义域关于原点对称
0
x
1
2
3
-1
-2
-3
1
2
3
4
5
6
y
解:
y=x2
性质:偶函数在关于原点对称的区间上
单调性相反.
问题:
是奇函数吗
解:
性质:奇函数的定义域关于原点对称
6.奇函数的性质特征
不是
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
f (x)=x
性质:奇函数在关于原点对称的区间上
单调性一致.
y=x3
0
三、巩固新知
1.例6 判断下列函数的奇偶性:
三、巩固新知
1.例6 判断下列函数的奇偶性:
是偶函数
是奇函数
不是奇函数也不是偶函数
非奇非偶函数
非奇非偶函数
既是奇函数也是偶函数
2.变式:判断下列函数的奇偶性:
是奇函数
3.思考:
x
y
1
2
3
1
2
3
-3
-3
-2
-1
0
-2
-1
已知y=f (x)是R上的奇函数,当x>0时,f (x)=x2 +2x-1 ,
求函数f (x)的表达式.
又∵ y=f(x)是R上的奇函数
.
4.能力提升:
(2). 如图是奇函数y=f (x)图象的一部分,
试画出函数在y轴左边的图象.
x
y
0
5.变式:
(1).证明函数 是奇函数.
2. 数形结合的思想方法
1. 知识结构
作业: 课本P86 习题3.2 5题
四、课堂小结
函数奇偶性
奇函数、偶函数
奇函数、偶函数的性质
奇函数、偶函数的图象特征
第一章 统计案例
3.2.2
奇 偶 性
高一数学必修第一册 第三章 函数的概念与性质
学习目标
1.理解函数奇偶性的概念和性质;
2.会判断简单函数的奇偶性;
3.学会运用函数图象理解和研究函数的性质.
4.核心素养:数学抽象、逻辑推理、数学运算.
一、引入新课
现实生活中的“美”的事例
x
y
O
f (x)=x2
g(x)=2-|x|
x … -2 -1 0 1 2 …
y … 4 1 0 1 4 …
x … -2 -1 0 1 2 …
y … 0 1 2 1 0 …
问题:
1).对定义域中的每一个x,
-x是否也在定义域内?
2). f (x)与f (-x)的值有什么
关系?
x
y
O
2
2
-2
二、探究新知
1.数学中的函数图象的“美”
函数y=f(x)的图象
关于 y轴对称
1.对定义域中的每一
个x,-x是也在定义域内
2.都有 f(x)=f(-x)
一般地,设函数f (x)的定义域为I,
如果 都有 且
f (-x)= f (x),
那么称函数y=f (x)是偶函数.
2.偶函数的概念:
偶函数的图象关于y轴对称
-1
x
y
O
1
2
2
1
3
4
-2
-1
x
y
O
1
2
0.01
0.02
-2
-3
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f (x)=x
观察下面两个函数的图象有什么特征?
两个函数的图象关于原点成中心对称图形
f (-3)= -3 =
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
……
f (-x) -f (x)
f (-1)= -1
f (-2)= -2 =
x
-x
-f (1)
=
-f (2)
-f (3)
=
x … -2 -1 0 1 2 …
f(x)=x … -2 -1 0 1 2 …
f (x)=x
函数f (x)=x的变化情况
f (-3)= =-f (3)
f (-1)= -1 =-f (1)
f (-2)= =-f (2)
……
3
2
1
0
-2
-3
x
-1
-1
函数 的变化情况
f (-x) -f (x)
=
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
1
函数y=f(x)的图象
关于 原点对称
1.对定义域中的每一
个x,-x是也在定义域内
2.都有 f(x)= — f(-x)
一般地,设函数f (x)的定义域为I,
如果 都有 且
f (-x)=- f (x),
那么称函数y=f (x)是奇函数.
3.奇函数的概念:
如果一个函数f (x)是奇函数或偶函数,
那么我们就说函数f (x)具有奇偶性.
①定义法:
先看定义域是否关于原点对称,
再看f (-x)与 f (x)的关系.
4.函数的奇偶性:
②图象法:
看图象是否关于原点或y轴对称.
判定函数奇偶性基本方法:
f (x)=0 , x∈R
说明:
1).根据函数的奇偶性
既奇又偶函数
非奇非偶函数
偶函数
奇函数
函数可划分为四类:
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)=0
既是奇函数又是偶函数
非奇非偶函数
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)=3x+1
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
-3
f(x)= x2+2x
2).奇、偶函数定义的逆命题也成立,即
若f (x)为奇函数,则f (-x)=-f (x)有成立.
若f (x)为偶函数,则f (-x)=f (x)有成立.
3).奇、偶函数性质:
偶函数的
定义域关于原点对称
图象关于y轴对称
奇函数的
定义域关于原点对称
图象关于原点对称.
如果一个函数是偶函数,则它的图象关于y轴对称.
y=x2
5.偶函数的性质特征
反过来,
如果一个函数的图象关于y轴对称,则这个函数为偶函数.
,
是偶函数吗
问题:
不是
性质:偶函数的定义域关于原点对称
0
x
1
2
3
-1
-2
-3
1
2
3
4
5
6
y
解:
y=x2
性质:偶函数在关于原点对称的区间上
单调性相反.
问题:
是奇函数吗
解:
性质:奇函数的定义域关于原点对称
6.奇函数的性质特征
不是
0
x
y
1
2
3
-1
-2
-1
1
2
3
-2
f (x)=x
性质:奇函数在关于原点对称的区间上
单调性一致.
y=x3
0
三、巩固新知
1.例6 判断下列函数的奇偶性:
三、巩固新知
1.例6 判断下列函数的奇偶性:
是偶函数
是奇函数
不是奇函数也不是偶函数
非奇非偶函数
非奇非偶函数
既是奇函数也是偶函数
2.变式:判断下列函数的奇偶性:
是奇函数
3.思考:
x
y
1
2
3
1
2
3
-3
-3
-2
-1
0
-2
-1
已知y=f (x)是R上的奇函数,当x>0时,f (x)=x2 +2x-1 ,
求函数f (x)的表达式.
又∵ y=f(x)是R上的奇函数
.
4.能力提升:
(2). 如图是奇函数y=f (x)图象的一部分,
试画出函数在y轴左边的图象.
x
y
0
5.变式:
(1).证明函数 是奇函数.
2. 数形结合的思想方法
1. 知识结构
作业: 课本P86 习题3.2 5题
四、课堂小结
函数奇偶性
奇函数、偶函数
奇函数、偶函数的性质
奇函数、偶函数的图象特征
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
