平行线的性质1[下学期]
文档属性
| 名称 | 平行线的性质1[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-09 00:00:00 | ||
图片预览







文档简介
课件22张PPT。平行线的性质判定两直线平行的方法有哪些?判定1:判定2:判定3:同位角相等,两直线平行。内错角相等,两直线平行。平行于同一条直线的两条直线平行。同旁内角互补,两直线平行。平行线定义:同一平面内,不相交 ` 的两条直线叫平行线。垂直于同一条直线的两条直线平行。∵ b⊥a , c⊥a (已知)
∴ ∠1=90°,∠2=90°( )
∴∠1 + ∠2= 180°
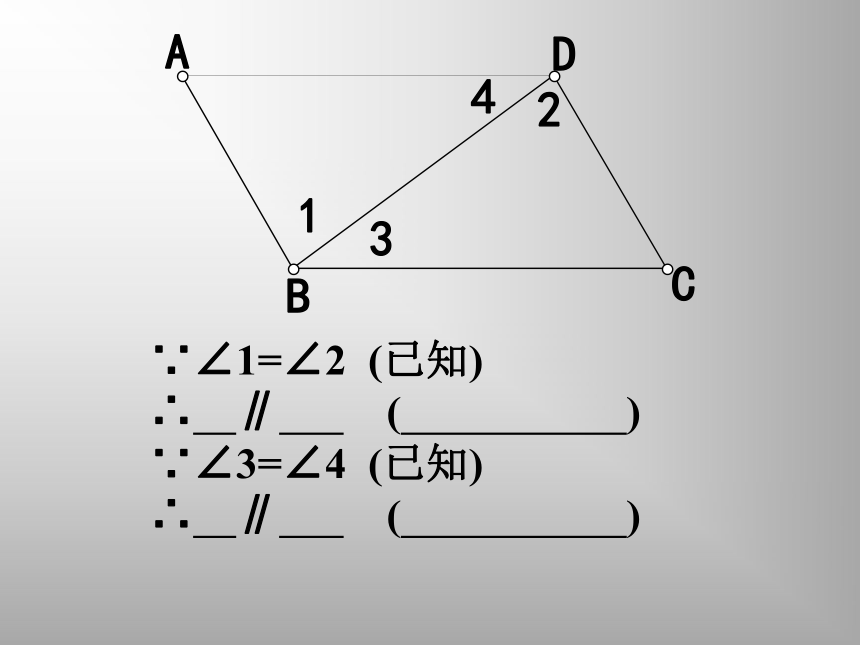
∴b∥c ( ) 课堂练习:垂直的定义同旁内角互补,两直线平行。∵∠1=∠2 (已知)
∴ ∥ ( )
∵∠3=∠4 (已知)
∴ ∥ ( )
∵∠B+∠1=180° (已知)
∴ ∥ ( )
又∵∠B=∠E (已知)
∠1=∠2 ( )
∴ + = ( )
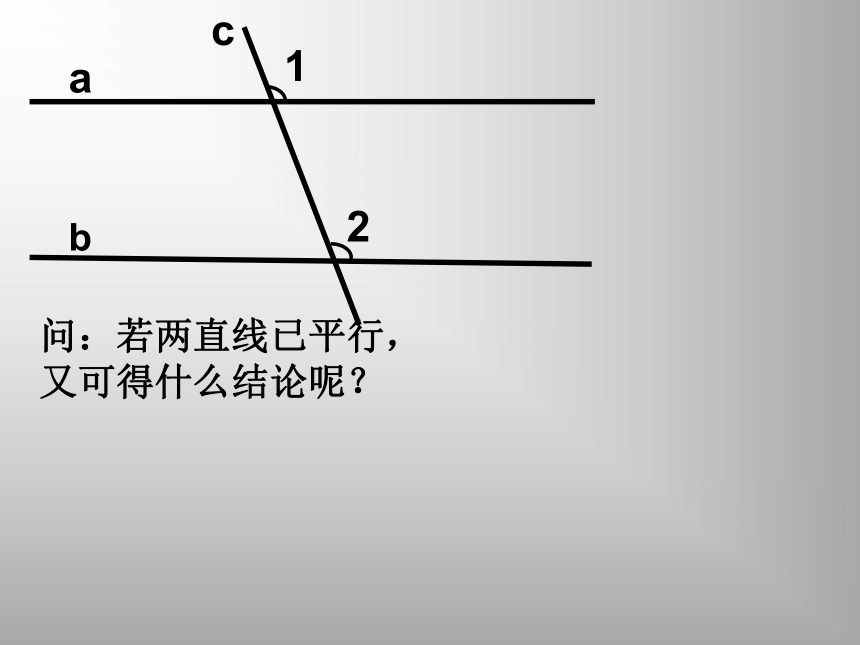
∴BC∥EF ( ) 21abc问:若两直线已平行, 又可得什么结论呢?
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的判定公理与
性质公理有什么不同比一比问:那内错角,同旁内角有没有相似的规律呢?平行线的性质:性质1:两直线平行,同位角相等。性质2:两直线平行,内错角相等。性质3:两直线平行,同旁内角互补
1、根据右边的图形,在括号内填上相应的理由:
(1)由于AB∥CD,根据 ,
可知∠3=∠C
(2)由于EC∥BD,根据 ,
可知∠3=∠B
(3)由于AB∥CD,根据 ,
可知∠2+∠C= 180°两直线平行,内错角相等两直线平行,同位角相等两直线平行,同旁内角互补2、如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?
(2)从∠1=110 °可以知道∠3是多少度?
(3)从∠1=110 °可以知道∠4是多少度?如图,
(1)如果AD∥BC,那么∠B=∠1吗?
(2)如果AB∥CD,那么∠D=∠1吗?解:由于AD∥BC,根据两直线平行,同位角相等,可知∠B=∠1。由于AB∥DC,根据两直线平行,内错角相等,可知∠D=∠1。3.如图,
如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC=180°.
DABBCD能力考查1如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???能力考查2如图:? AB//DE(已知)
? ABE+ =180?
( )
? AB// (已知)
? DEC= ? ABC
( )????两直线平行,同旁内角互补两直线平行,同位角相等?DEBEF下面是平行线性质的简单应用例1:已知:直线a∥b, c∥d, ∠1=115°,
求: ∠2、∠3的度数
例2:已知: ∠ 1=130 °, ∠2=50 °,
∠3=60 °,
求:∠4等于多少度?
例3CBAD如图是梯形有上底的一部分。
已经量得? A= 115°,?D=100°,
梯形另外两个角各是多少度?
如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
分析:将实际问题转换为数学问题
已知: AB ∥ CD, ∠B=142°
求: ∠C=?生活数学2:已知角之间的关系,得到两直线平行的结论
是平行线的判定。
已知两直线平行,得到角之间的关系的结论
是平行线的性质。小结判定:两直线平行两直线平行性质:同位角相等内错角相等同旁内角互补同位角相等内错角相等同旁内角互补
∴ ∠1=90°,∠2=90°( )
∴∠1 + ∠2= 180°
∴b∥c ( ) 课堂练习:垂直的定义同旁内角互补,两直线平行。∵∠1=∠2 (已知)
∴ ∥ ( )
∵∠3=∠4 (已知)
∴ ∥ ( )
∵∠B+∠1=180° (已知)
∴ ∥ ( )
又∵∠B=∠E (已知)
∠1=∠2 ( )
∴ + = ( )
∴BC∥EF ( ) 21abc问:若两直线已平行, 又可得什么结论呢?
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的判定公理与
性质公理有什么不同比一比问:那内错角,同旁内角有没有相似的规律呢?平行线的性质:性质1:两直线平行,同位角相等。性质2:两直线平行,内错角相等。性质3:两直线平行,同旁内角互补
1、根据右边的图形,在括号内填上相应的理由:
(1)由于AB∥CD,根据 ,
可知∠3=∠C
(2)由于EC∥BD,根据 ,
可知∠3=∠B
(3)由于AB∥CD,根据 ,
可知∠2+∠C= 180°两直线平行,内错角相等两直线平行,同位角相等两直线平行,同旁内角互补2、如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?
(2)从∠1=110 °可以知道∠3是多少度?
(3)从∠1=110 °可以知道∠4是多少度?如图,
(1)如果AD∥BC,那么∠B=∠1吗?
(2)如果AB∥CD,那么∠D=∠1吗?解:由于AD∥BC,根据两直线平行,同位角相等,可知∠B=∠1。由于AB∥DC,根据两直线平行,内错角相等,可知∠D=∠1。3.如图,
如果AD∥BC,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,可得∠____+∠ABC=180°.
DABBCD能力考查1如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???能力考查2如图:? AB//DE(已知)
? ABE+ =180?
( )
? AB// (已知)
? DEC= ? ABC
( )????两直线平行,同旁内角互补两直线平行,同位角相等?DEBEF下面是平行线性质的简单应用例1:已知:直线a∥b, c∥d, ∠1=115°,
求: ∠2、∠3的度数
例2:已知: ∠ 1=130 °, ∠2=50 °,
∠3=60 °,
求:∠4等于多少度?
例3CBAD如图是梯形有上底的一部分。
已经量得? A= 115°,?D=100°,
梯形另外两个角各是多少度?
如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
分析:将实际问题转换为数学问题
已知: AB ∥ CD, ∠B=142°
求: ∠C=?生活数学2:已知角之间的关系,得到两直线平行的结论
是平行线的判定。
已知两直线平行,得到角之间的关系的结论
是平行线的性质。小结判定:两直线平行两直线平行性质:同位角相等内错角相等同旁内角互补同位角相等内错角相等同旁内角互补
