数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共44张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.1.1椭圆及其标准方程 课件(共44张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 15:48:27 | ||
图片预览








文档简介
(共44张PPT)
3.1.1 椭圆及其标准方程
第一课时
第三章 圆锥曲线的方程
1.了解椭圆的实际背景,理解从具体情境中抽象出椭圆的过程.
2.通过对椭圆标准方程的推导,进一步体会数形结合的思想.
3.掌握椭圆的定义与标准方程.(重点、难点)
学习目标
复习引入
圆的定义是什么?
平面内到定点的距离等于定长的点的集合是圆。
圆的标准方程是什么?
把圆”压扁“得到什么图形
——“传说中的”飞碟
太阳系行星的运动
探究一:椭圆的定义
实验2:把细绳的两端拉开一段距离,分别固定在图板的两点F1,F2(要求绳长要大于两定点的距离),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
实验1 取出事先准备好的一条定长的细绳和一个图板,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖是一个动点,笔尖画出的轨迹是一个图形?
课前准备:一根直尺,两个图钉,一根绳子,一只铅笔
圆
椭圆
数学实验
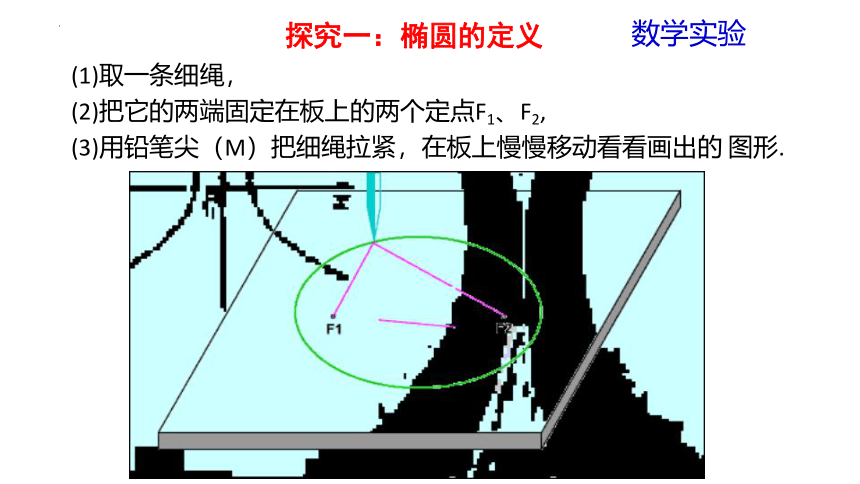
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2,
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的 图形.
探究一:椭圆的定义
说明:(1)由于绳长固定,所以点M到两个定点的距离和是个定值;
根据上面的内容你能给
出椭圆的定义吗?
思考1:①在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
②在画椭圆的过程中,绳子的长度变了没有?说明了什么?
③在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
(2)点M到两个定点的距离和要大于两个定点之间的距离。
探究一:椭圆的定义
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
两个定点F1,F2叫做椭圆的焦点;两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距。
思考2:若动点M与两个定点F1,F2的距离的和等于|F1F2|, 动点的轨迹是什么?
线段F1F2
思考3:若动点M与两个定点F1,F2的距离的和小于|F1F2|,动点的轨迹是什么?
轨迹不存在
F2
F1
M
符号表述为:{M||MF1| +| MF2|= 2a ,2a> |F1F2|}
说明:椭圆的定义的正逆用:一方面,符合定义条件的动点的轨迹为椭圆;另一方面,椭圆上所有的点一定满足定义的条件(即到两焦点的距离之和为常数).
探究一:椭圆的定义
例1、下列说法正确的是( )
A.到F1(-3,0),F2(3,0)两点的距离之和等于6的点的轨迹是椭圆;
B.到F1(-3,0),F2(3,0)两点的距离之和为4的点的轨迹是椭圆;
C.到F1(-3,0),F2(3,0)两点的距离之和等于10的点的轨迹是椭圆;
D.到F1(-3,0),F2(3,0)距离相等的点的轨迹是椭圆。
解析:A 线段F1F2; B 轨迹不存在; C,根据椭圆的定义,知轨迹是椭圆;D中,点的轨迹是线段F1F2的垂直平分线。
C
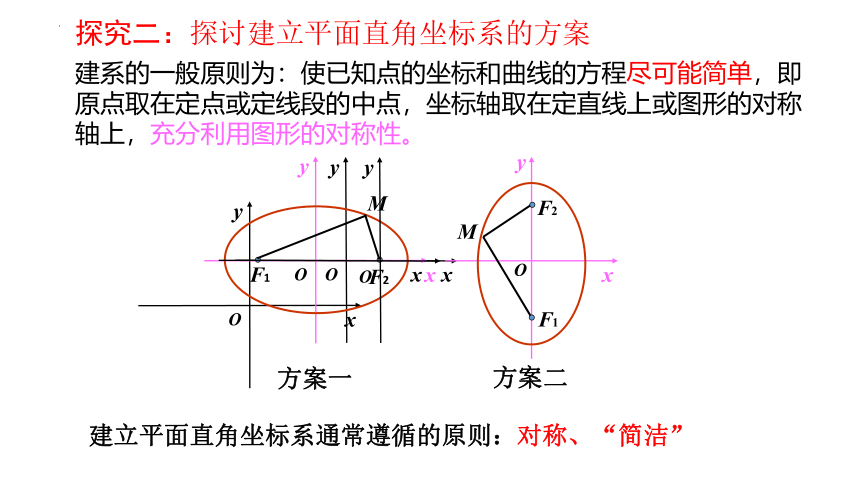
探究二:探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
建系的一般原则为:使已知点的坐标和曲线的方程尽可能简单,即原点取在定点或定线段的中点,坐标轴取在定直线上或图形的对称轴上,充分利用图形的对称性。
1.建系:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系。
2.设点:设M(x,y)是椭圆上任一点,椭圆的焦距为2c(c>0),M与F1、F2的距离的和等于常数2a(a>0),则F1(—c,0)、F2(c,0)。
3.列式:由定义知:
(
)
(
)
2
2
2
2
2
1
y
c
x
MF
y
c
x
MF
+
-
=
+
+
=
∵
(
)
(
)
a
y
c
x
y
c
x
2
2
2
2
2
=
+
-
+
+
+
4.化简:将方程移项后平方得:
两边再平方得:
探究三、椭圆标准方程的推导:
由椭圆定义知:2a>2c,即a>c,a2-c2>0
两边同除以 a2b2得:
这个方程叫做椭圆的标准方程,它所表示的椭圆的焦点在x轴上。
它也是椭圆的标准方程。
理解:所谓椭圆标准方程,一定指的是焦点在坐标轴上,且两焦点的中点为坐标原点.
设参量b的意义:①便于写出椭圆的标准方程;②a,b,c的关系有明显的几何意义,a2=b2+c2(b>0)
设a2—c2=b2(b>0) 得
b2x2+a2y2=a2b2
若椭圆焦点F1(0,—c),F2(0,c)在y轴上,因为这时x轴与y轴交换,所以只要把方程中的x,y互换即可得方程:
y
x
o
F
2
F
1
M
观察下图,你能从中找出表示a,b,c的线段吗?
探究四:椭圆中a,b,c的意义
a、b、c都有特定的意义:
a — 椭圆上任意一点P到F1、F2距离和的一半;
c — 半焦距.有关系式a2=b2+c2成立。
a
b
c
y
o
F1
F
P
x
a
b
c
方
程
特
点
(2)在椭圆两种标准方程中,总有a>b>0;(a最大)
(4)a、b、c都有特定的意义:
a—椭圆上任意一点P到F1、F2距离和的一半;
c—半焦距.有关系式a2=b2+c2成立。
探究五:解读椭圆的两个标准方程
(3)焦点在分母大的变量所对应的那个轴上;“谁大在谁上”。
(1)方程的左边是两项平方和的形式,等号的右边是1;
y
x
o
F
2
F
1
M
y
o
F
1
F
2
M
x
x轴,焦点坐标为(-3,0)和(3,0)
例2、判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标。
y 轴,焦点坐标为(0,-2)和(0,2)
判断椭圆的焦点在哪个轴上的准则:
哪个分母大,焦点就在哪条轴上,大的分母就是a2.
口诀:椭圆方程有特点,系数为正加相连,
分母较大定焦点,右边数“1”记心间。
将方程化成标准方程为:
a2=16,b2=8,
所以椭圆的焦点为:
焦点在y 轴上
求椭圆的标准方程的步骤:
1.确定焦点在那条轴上;
2.设出椭圆的标准方程;
3.用待定系数法或定义法求出a、b(或a2,b2)的值,
写出椭圆的标准方程.
解: 2a=10,2c=8, a=5,c=4.
b2=a2—c2=52—42=9
因为椭圆的焦点在x轴上,所以它的标准方程为:
例3、已知椭圆的焦点在x轴上,焦距为8,椭圆上的点到两个焦点的距离之和为10, 求该椭圆的标准方程.
一定焦点位置;二设椭圆方程;三求a、b的值.
例4、已知椭圆两个焦点的坐标分别是(—2,0),(2,0),并且椭圆经过点
求它的标准方程
分析:求椭圆的标准方程关键是确定焦点的位置及a,b的值
例5、
解:
平面内到两个定点F1,F2的距离和等于常数2a(大于|F1F2|)的点的轨迹
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2=b2+c2(a最大)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
焦点在x轴上
焦点在y轴上
小结:
作业:p109练习1、2
3.1.1 椭圆及其标准方程
第二课时
第三章 圆锥曲线的方程
1.了解椭圆的实际背景,理解从具体情境中抽象出椭圆的过程.
2.通过对椭圆标准方程的推导,进一步体会数形结合的思想.
3.掌握椭圆的定义与标准方程.(重点、难点)
学习目标
平面内到两个定点F1,F2的距离和等于常数2a(大于|F1F2|)的点的轨迹,两焦点间的距离|F1F2|叫做焦距。
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2=b2+c2(a最大)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
焦点在x轴上
焦点在y轴上
复习回顾1:
方
程
特
点
(2)在椭圆两种标准方程中,总有a>b>0;(a最大)
(4)a、b、c都有特定的意义:
a—椭圆上任意一点P到F1、F2距离和的一半;
c—半焦距.有关系式a2=b2+c2成立。
复习回顾2:椭圆的两个标准方程
(3)焦点在分母大的变量所对应的那个轴上;“谁大在谁上”。
(1)方程的左边是两项平方和的形式,等号的右边是1;
y
x
o
F
2
F
1
M
y
o
F
1
F
2
M
x
求椭圆标准方程的方法:
(1)定义法:根据椭圆定义,确定a2,b2的值,结合焦点位置写出椭圆方程.
(2)待定系数法:先判断焦点位置,设出标准方程形式,最后由条件确定待定系数即可.即“先定位,后定量”.
当所求椭圆的焦点位置不能确定时,应按焦点在x轴上和焦点在y轴上进行分类讨论,但要注意a>b>0这一条件.
(3)当已知椭圆经过两点,求椭圆的标准方程时,可把椭圆的方程设成
mx2+ny2=1(m>0,n>0且m≠n) (统一方程)
有两个优点:①列出的方程组中分母不含分母;
②不用讨论焦点所在的位置,从而简化求解过程.
课前练习1、下列方程哪些表示椭圆?
D
例2、如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?(当P经过圆与x轴的交点时,规定点M与点P重合。)
y
x
o
将圆按照某个方向均匀地压缩(拉长),可以得到椭圆.
分析:点P在圆x2+y2=4上运动,点P的运动引起点M运动,则称点P是点M的相关点,我们可以由M为线段PD的中点得到点M与点P坐标之间的关系式,并由点P的坐标满足圆的方程得到点M的坐标所满足的方程。
探究一:求轨迹方程的方法——相关点法
所以点M的轨迹是椭圆.
o
x
y
P
M
D
寻求点M的坐标(x,y)中x,y与x0,y0之间的关系,然后消去x0,y0,得到点M的轨迹方程。这是解析几何中求点的轨迹方程常用的方法.称为相关点法(或代点法)
解:设点M的坐标为(x,y),点P的坐标为(x0,y0),则点D的坐标为(x0,0).
由点M是线段PD的中点,得
(1)设点:设所求轨迹上动点坐标为M(x,y),已知曲线上动点坐标为P(x0,y0).
(3)代换:将上述关系式代入点P所在的曲线方程得到所求动点轨迹的方程,并把所得方程化简即可.
说明:(相关点法或代点法)如果一个动点M随着另一个在已知曲线上运动的动点P(相关点)而运动,则求M点的轨迹方程时一般用代点法来求解.基本步骤为:
(2)求关系式:用点M的坐标表示出点P的坐标;
例3、如图,设点A,B的坐标分别为(—5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是 ,求点M的轨迹方程.
分析:把题目条件直接用x,y表示出来,x,y之间的关系式就显示出来了.
变式:课本P109 T4
点M的轨迹是除去(—5,0),(5,0)两点的椭圆.
探究二:求轨迹方程的方法——直接法
求轨迹方程的常用方法
1.直接法
根据已知条件直接列出动点满足的关系式,进而求得轨迹方程
2.定义法
熟练掌握一些常用图形轨迹的定义,如圆、椭圆、双曲线等,利用
定义求得轨迹方程
3.相关点代入法
某个动点P在已知方程的曲线上移动,另一个动点M随着P的变化而变化,这两个点具有相关性
探究三:利用椭圆的标准方程求参数的取值范围
探究四:椭圆中的焦点三角形问题
例5 椭圆 ,点P是椭圆上一点,F1,F2是椭圆的左、右
焦点,且∠PF1F2=120°,则△PF1F2的面积为________.
定义:椭圆上一点和两个焦点构成的三角形,
称之为椭圆的焦点三角形。
例6 椭圆 ,点P在椭圆上运动,F1,F2是椭圆的左、右焦点,
则 的最大值为是( )
y
o
F
1
F
2
P(x0,y0)
x
性质一:该三角形一边长为焦距,另两边的和为定值。所以周长为定值2a+2c。
性质二:若椭圆方程为
两焦点分别为F1,F2,设焦点△PF1F2中∠F1PF2=θ,P点的坐标为(x0,y0),则焦点△PF1F2的面积为
θ
总结:椭圆中的焦点三角形有关的性质
M
N
三
性质二证明:
y
o
F
1
F
2
P(x0,y0)
x
另过P点作x轴的垂线,y0是焦点△PF1F2底边F1F2上的高,
所以焦点△PF1F2的面积=
结论(1)
(2)当P点在椭圆与y轴的交点时,焦点三角形面积最大为bc。
θ
性质四:当点P从右至左运动时,∠F1PF2=θ由锐角变成直角,又变成钝角,过了Y轴之后,对称地由钝角变成直角,再变成锐角,并且发现当点P与椭圆与y轴的交点重合时,∠F1PF2达到最大。
证明:
当且仅当m=n,即P与椭圆与y轴的交点重合时,“=”成立,此时cosθ取的最小值,而角θ取得最大值。
y
o
F
1
F
2
P(x0,y0)
x
作业布置:课本P109:练习1--4
3.1.1 椭圆及其标准方程
第一课时
第三章 圆锥曲线的方程
1.了解椭圆的实际背景,理解从具体情境中抽象出椭圆的过程.
2.通过对椭圆标准方程的推导,进一步体会数形结合的思想.
3.掌握椭圆的定义与标准方程.(重点、难点)
学习目标
复习引入
圆的定义是什么?
平面内到定点的距离等于定长的点的集合是圆。
圆的标准方程是什么?
把圆”压扁“得到什么图形
——“传说中的”飞碟
太阳系行星的运动
探究一:椭圆的定义
实验2:把细绳的两端拉开一段距离,分别固定在图板的两点F1,F2(要求绳长要大于两定点的距离),套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?
实验1 取出事先准备好的一条定长的细绳和一个图板,把它的两端都固定在图板的同一点,套上铅笔,拉紧绳子,移动笔尖,这时笔尖是一个动点,笔尖画出的轨迹是一个图形?
课前准备:一根直尺,两个图钉,一根绳子,一只铅笔
圆
椭圆
数学实验
(1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2,
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的 图形.
探究一:椭圆的定义
说明:(1)由于绳长固定,所以点M到两个定点的距离和是个定值;
根据上面的内容你能给
出椭圆的定义吗?
思考1:①在椭圆形成的过程中,细绳的两端的位置是固定的还是运动的?
②在画椭圆的过程中,绳子的长度变了没有?说明了什么?
③在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关系?
(2)点M到两个定点的距离和要大于两个定点之间的距离。
探究一:椭圆的定义
平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
两个定点F1,F2叫做椭圆的焦点;两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距。
思考2:若动点M与两个定点F1,F2的距离的和等于|F1F2|, 动点的轨迹是什么?
线段F1F2
思考3:若动点M与两个定点F1,F2的距离的和小于|F1F2|,动点的轨迹是什么?
轨迹不存在
F2
F1
M
符号表述为:{M||MF1| +| MF2|= 2a ,2a> |F1F2|}
说明:椭圆的定义的正逆用:一方面,符合定义条件的动点的轨迹为椭圆;另一方面,椭圆上所有的点一定满足定义的条件(即到两焦点的距离之和为常数).
探究一:椭圆的定义
例1、下列说法正确的是( )
A.到F1(-3,0),F2(3,0)两点的距离之和等于6的点的轨迹是椭圆;
B.到F1(-3,0),F2(3,0)两点的距离之和为4的点的轨迹是椭圆;
C.到F1(-3,0),F2(3,0)两点的距离之和等于10的点的轨迹是椭圆;
D.到F1(-3,0),F2(3,0)距离相等的点的轨迹是椭圆。
解析:A 线段F1F2; B 轨迹不存在; C,根据椭圆的定义,知轨迹是椭圆;D中,点的轨迹是线段F1F2的垂直平分线。
C
探究二:探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
建系的一般原则为:使已知点的坐标和曲线的方程尽可能简单,即原点取在定点或定线段的中点,坐标轴取在定直线上或图形的对称轴上,充分利用图形的对称性。
1.建系:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系。
2.设点:设M(x,y)是椭圆上任一点,椭圆的焦距为2c(c>0),M与F1、F2的距离的和等于常数2a(a>0),则F1(—c,0)、F2(c,0)。
3.列式:由定义知:
(
)
(
)
2
2
2
2
2
1
y
c
x
MF
y
c
x
MF
+
-
=
+
+
=
∵
(
)
(
)
a
y
c
x
y
c
x
2
2
2
2
2
=
+
-
+
+
+
4.化简:将方程移项后平方得:
两边再平方得:
探究三、椭圆标准方程的推导:
由椭圆定义知:2a>2c,即a>c,a2-c2>0
两边同除以 a2b2得:
这个方程叫做椭圆的标准方程,它所表示的椭圆的焦点在x轴上。
它也是椭圆的标准方程。
理解:所谓椭圆标准方程,一定指的是焦点在坐标轴上,且两焦点的中点为坐标原点.
设参量b的意义:①便于写出椭圆的标准方程;②a,b,c的关系有明显的几何意义,a2=b2+c2(b>0)
设a2—c2=b2(b>0) 得
b2x2+a2y2=a2b2
若椭圆焦点F1(0,—c),F2(0,c)在y轴上,因为这时x轴与y轴交换,所以只要把方程中的x,y互换即可得方程:
y
x
o
F
2
F
1
M
观察下图,你能从中找出表示a,b,c的线段吗?
探究四:椭圆中a,b,c的意义
a、b、c都有特定的意义:
a — 椭圆上任意一点P到F1、F2距离和的一半;
c — 半焦距.有关系式a2=b2+c2成立。
a
b
c
y
o
F1
F
P
x
a
b
c
方
程
特
点
(2)在椭圆两种标准方程中,总有a>b>0;(a最大)
(4)a、b、c都有特定的意义:
a—椭圆上任意一点P到F1、F2距离和的一半;
c—半焦距.有关系式a2=b2+c2成立。
探究五:解读椭圆的两个标准方程
(3)焦点在分母大的变量所对应的那个轴上;“谁大在谁上”。
(1)方程的左边是两项平方和的形式,等号的右边是1;
y
x
o
F
2
F
1
M
y
o
F
1
F
2
M
x
x轴,焦点坐标为(-3,0)和(3,0)
例2、判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标。
y 轴,焦点坐标为(0,-2)和(0,2)
判断椭圆的焦点在哪个轴上的准则:
哪个分母大,焦点就在哪条轴上,大的分母就是a2.
口诀:椭圆方程有特点,系数为正加相连,
分母较大定焦点,右边数“1”记心间。
将方程化成标准方程为:
a2=16,b2=8,
所以椭圆的焦点为:
焦点在y 轴上
求椭圆的标准方程的步骤:
1.确定焦点在那条轴上;
2.设出椭圆的标准方程;
3.用待定系数法或定义法求出a、b(或a2,b2)的值,
写出椭圆的标准方程.
解: 2a=10,2c=8, a=5,c=4.
b2=a2—c2=52—42=9
因为椭圆的焦点在x轴上,所以它的标准方程为:
例3、已知椭圆的焦点在x轴上,焦距为8,椭圆上的点到两个焦点的距离之和为10, 求该椭圆的标准方程.
一定焦点位置;二设椭圆方程;三求a、b的值.
例4、已知椭圆两个焦点的坐标分别是(—2,0),(2,0),并且椭圆经过点
求它的标准方程
分析:求椭圆的标准方程关键是确定焦点的位置及a,b的值
例5、
解:
平面内到两个定点F1,F2的距离和等于常数2a(大于|F1F2|)的点的轨迹
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2=b2+c2(a最大)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
焦点在x轴上
焦点在y轴上
小结:
作业:p109练习1、2
3.1.1 椭圆及其标准方程
第二课时
第三章 圆锥曲线的方程
1.了解椭圆的实际背景,理解从具体情境中抽象出椭圆的过程.
2.通过对椭圆标准方程的推导,进一步体会数形结合的思想.
3.掌握椭圆的定义与标准方程.(重点、难点)
学习目标
平面内到两个定点F1,F2的距离和等于常数2a(大于|F1F2|)的点的轨迹,两焦点间的距离|F1F2|叫做焦距。
标准方程
相 同 点
焦点位置的判断
不 同 点
图 形
焦点坐标
定 义
a、b、c 的关系
x
y
F1
F2
P
O
x
y
F1
F2
P
O
a2=b2+c2(a最大)
看分母的大小,焦点在分母大的那一项对应的坐标轴上.
焦点在x轴上
焦点在y轴上
复习回顾1:
方
程
特
点
(2)在椭圆两种标准方程中,总有a>b>0;(a最大)
(4)a、b、c都有特定的意义:
a—椭圆上任意一点P到F1、F2距离和的一半;
c—半焦距.有关系式a2=b2+c2成立。
复习回顾2:椭圆的两个标准方程
(3)焦点在分母大的变量所对应的那个轴上;“谁大在谁上”。
(1)方程的左边是两项平方和的形式,等号的右边是1;
y
x
o
F
2
F
1
M
y
o
F
1
F
2
M
x
求椭圆标准方程的方法:
(1)定义法:根据椭圆定义,确定a2,b2的值,结合焦点位置写出椭圆方程.
(2)待定系数法:先判断焦点位置,设出标准方程形式,最后由条件确定待定系数即可.即“先定位,后定量”.
当所求椭圆的焦点位置不能确定时,应按焦点在x轴上和焦点在y轴上进行分类讨论,但要注意a>b>0这一条件.
(3)当已知椭圆经过两点,求椭圆的标准方程时,可把椭圆的方程设成
mx2+ny2=1(m>0,n>0且m≠n) (统一方程)
有两个优点:①列出的方程组中分母不含分母;
②不用讨论焦点所在的位置,从而简化求解过程.
课前练习1、下列方程哪些表示椭圆?
D
例2、如图,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?(当P经过圆与x轴的交点时,规定点M与点P重合。)
y
x
o
将圆按照某个方向均匀地压缩(拉长),可以得到椭圆.
分析:点P在圆x2+y2=4上运动,点P的运动引起点M运动,则称点P是点M的相关点,我们可以由M为线段PD的中点得到点M与点P坐标之间的关系式,并由点P的坐标满足圆的方程得到点M的坐标所满足的方程。
探究一:求轨迹方程的方法——相关点法
所以点M的轨迹是椭圆.
o
x
y
P
M
D
寻求点M的坐标(x,y)中x,y与x0,y0之间的关系,然后消去x0,y0,得到点M的轨迹方程。这是解析几何中求点的轨迹方程常用的方法.称为相关点法(或代点法)
解:设点M的坐标为(x,y),点P的坐标为(x0,y0),则点D的坐标为(x0,0).
由点M是线段PD的中点,得
(1)设点:设所求轨迹上动点坐标为M(x,y),已知曲线上动点坐标为P(x0,y0).
(3)代换:将上述关系式代入点P所在的曲线方程得到所求动点轨迹的方程,并把所得方程化简即可.
说明:(相关点法或代点法)如果一个动点M随着另一个在已知曲线上运动的动点P(相关点)而运动,则求M点的轨迹方程时一般用代点法来求解.基本步骤为:
(2)求关系式:用点M的坐标表示出点P的坐标;
例3、如图,设点A,B的坐标分别为(—5,0),(5,0).直线AM,BM相交于点M,且它们的斜率之积是 ,求点M的轨迹方程.
分析:把题目条件直接用x,y表示出来,x,y之间的关系式就显示出来了.
变式:课本P109 T4
点M的轨迹是除去(—5,0),(5,0)两点的椭圆.
探究二:求轨迹方程的方法——直接法
求轨迹方程的常用方法
1.直接法
根据已知条件直接列出动点满足的关系式,进而求得轨迹方程
2.定义法
熟练掌握一些常用图形轨迹的定义,如圆、椭圆、双曲线等,利用
定义求得轨迹方程
3.相关点代入法
某个动点P在已知方程的曲线上移动,另一个动点M随着P的变化而变化,这两个点具有相关性
探究三:利用椭圆的标准方程求参数的取值范围
探究四:椭圆中的焦点三角形问题
例5 椭圆 ,点P是椭圆上一点,F1,F2是椭圆的左、右
焦点,且∠PF1F2=120°,则△PF1F2的面积为________.
定义:椭圆上一点和两个焦点构成的三角形,
称之为椭圆的焦点三角形。
例6 椭圆 ,点P在椭圆上运动,F1,F2是椭圆的左、右焦点,
则 的最大值为是( )
y
o
F
1
F
2
P(x0,y0)
x
性质一:该三角形一边长为焦距,另两边的和为定值。所以周长为定值2a+2c。
性质二:若椭圆方程为
两焦点分别为F1,F2,设焦点△PF1F2中∠F1PF2=θ,P点的坐标为(x0,y0),则焦点△PF1F2的面积为
θ
总结:椭圆中的焦点三角形有关的性质
M
N
三
性质二证明:
y
o
F
1
F
2
P(x0,y0)
x
另过P点作x轴的垂线,y0是焦点△PF1F2底边F1F2上的高,
所以焦点△PF1F2的面积=
结论(1)
(2)当P点在椭圆与y轴的交点时,焦点三角形面积最大为bc。
θ
性质四:当点P从右至左运动时,∠F1PF2=θ由锐角变成直角,又变成钝角,过了Y轴之后,对称地由钝角变成直角,再变成锐角,并且发现当点P与椭圆与y轴的交点重合时,∠F1PF2达到最大。
证明:
当且仅当m=n,即P与椭圆与y轴的交点重合时,“=”成立,此时cosθ取的最小值,而角θ取得最大值。
y
o
F
1
F
2
P(x0,y0)
x
作业布置:课本P109:练习1--4
