平行线的性质与判定(习题课)[下学期]
文档属性
| 名称 | 平行线的性质与判定(习题课)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-02-27 13:01:00 | ||
图片预览


文档简介
课件17张PPT。平行线的判定与性质(习题课)
区别:条件与结论互换,
即:已知平行用性质,探索平行用判定。
平行线的判定方法:平行线的性质:两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补; 同位角相等,两直线平行;
内错角相等,两直线平行;
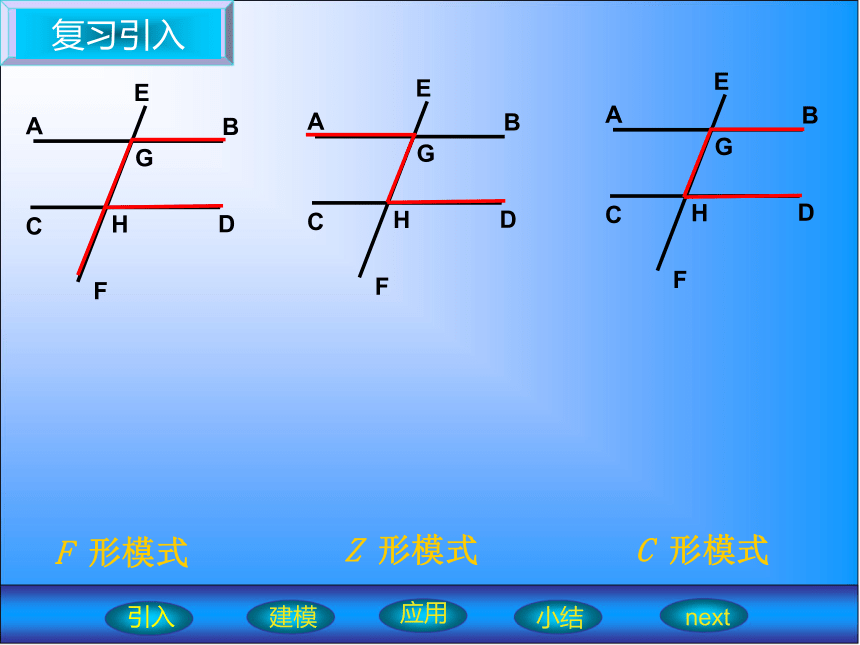
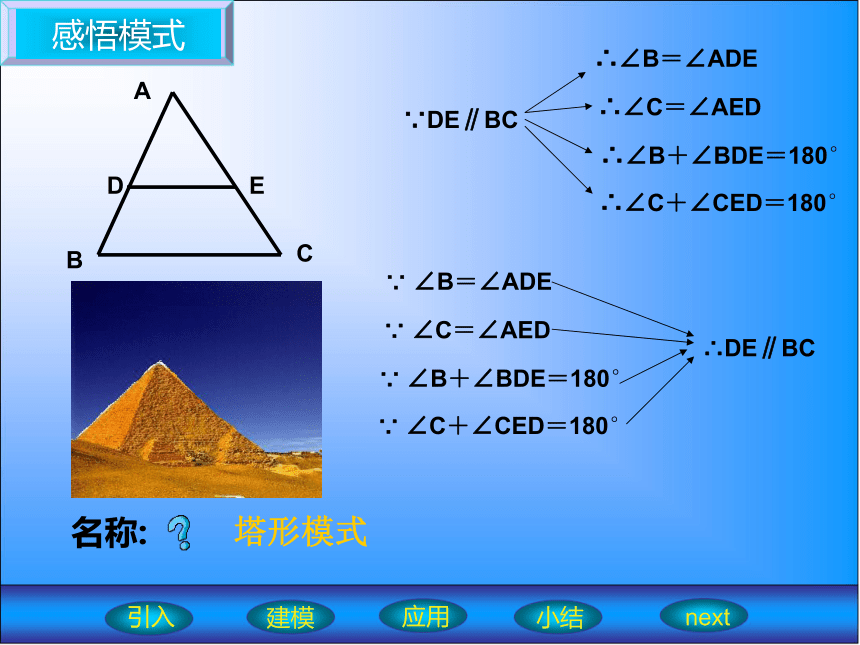
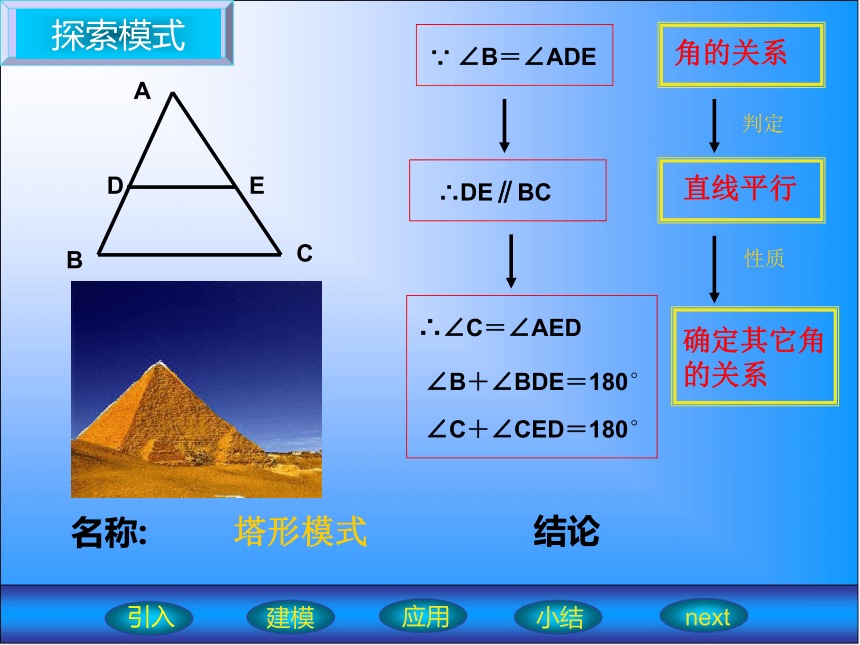
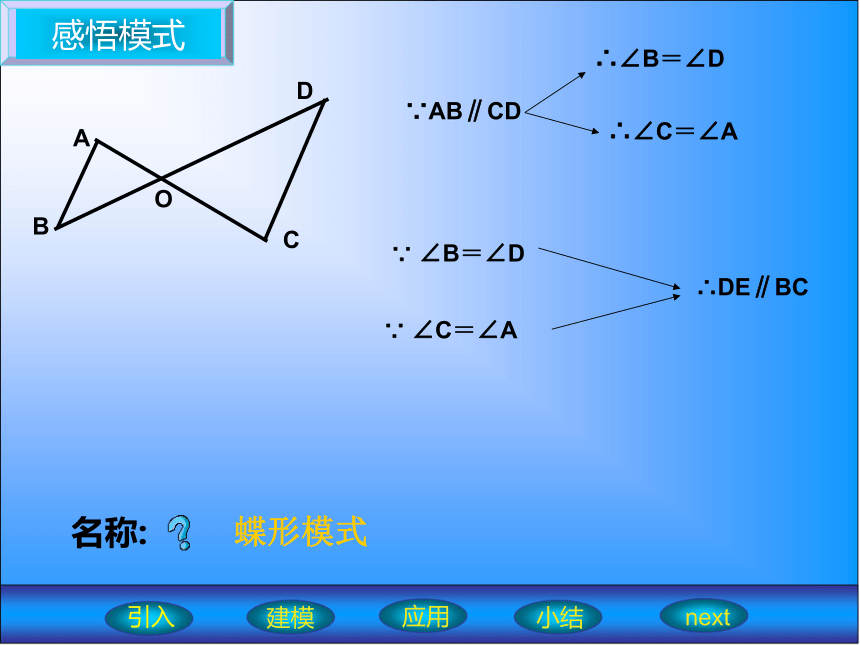
同旁内角互补,两直线平行;平行于同一直线的两直线平行。复习引入引入建模应用小结nextF 形模式Z 形模式C 形模式感悟模式∵DE∥BC∴DE∥BC名称:塔形模式建模应用小结next引入探索模式ABCDE名称:塔形模式结论建模应用小结next引入感悟模式ABCDO∵AB∥CD∵ ∠B=∠D∵ ∠C=∠A∴DE∥BC名称:蝶形模式建模应用小结next引入探索模式ABCDO名称:蝶形模式结论建模应用小结next引入应用模式ABCDEF123塔形模式Z 形模式塔形模式建模应用小结next引入应用模式 如图,若AB∥DF,∠2=∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2建模应用小结next引入应用模式如图,图中包含哪些基本模式?ABCDEFO建模应用小结next引入应用模式 已知,如图AB∥EF∥CD,AD∥BC,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D建模应用小结next引入应用模式①下图中包含哪些基本模式?②已知:∠1=∠2,∠C=∠D,
求证:DF∥AC③已知:∠A=∠F,∠C=∠D,
求证:DB∥ECABCDEF12建模应用小结next引入大众图标可以看作两个相同的“V”字型组成,下图给出一个“V”和O点.你能利用尺规作图补充完整吗?考考你:
图中如果AC∥BD 、AE ∥BF ,那么 ∠A与∠B的关系如何?你是怎样思考的?AC∥BD, AE ∥BF∠A=∠B操作与解释:数学课上有这样一道题:“如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?”。小王说“一定平行”;而小李说“不一定平行”。你更赞同谁的观点?
探索与思考:有一条直的等宽纸带,按如图所示折叠时,∠1=30°求纸带重叠部分中∠CAB的度数。已知:AB∥CD。试探索
①∠A、∠C与∠AEC之间的关系;
②∠B、∠D与∠BFD之间的关系。几 何
之 旅
即:已知平行用性质,探索平行用判定。
平行线的判定方法:平行线的性质:两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补; 同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;平行于同一直线的两直线平行。复习引入引入建模应用小结nextF 形模式Z 形模式C 形模式感悟模式∵DE∥BC∴DE∥BC名称:塔形模式建模应用小结next引入探索模式ABCDE名称:塔形模式结论建模应用小结next引入感悟模式ABCDO∵AB∥CD∵ ∠B=∠D∵ ∠C=∠A∴DE∥BC名称:蝶形模式建模应用小结next引入探索模式ABCDO名称:蝶形模式结论建模应用小结next引入应用模式ABCDEF123塔形模式Z 形模式塔形模式建模应用小结next引入应用模式 如图,若AB∥DF,∠2=∠A,试确定DE与AC的位置关系,并说明理由.ABCDEF2建模应用小结next引入应用模式如图,图中包含哪些基本模式?ABCDEFO建模应用小结next引入应用模式 已知,如图AB∥EF∥CD,AD∥BC,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D建模应用小结next引入应用模式①下图中包含哪些基本模式?②已知:∠1=∠2,∠C=∠D,
求证:DF∥AC③已知:∠A=∠F,∠C=∠D,
求证:DB∥ECABCDEF12建模应用小结next引入大众图标可以看作两个相同的“V”字型组成,下图给出一个“V”和O点.你能利用尺规作图补充完整吗?考考你:
图中如果AC∥BD 、AE ∥BF ,那么 ∠A与∠B的关系如何?你是怎样思考的?AC∥BD, AE ∥BF∠A=∠B操作与解释:数学课上有这样一道题:“如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?”。小王说“一定平行”;而小李说“不一定平行”。你更赞同谁的观点?
探索与思考:有一条直的等宽纸带,按如图所示折叠时,∠1=30°求纸带重叠部分中∠CAB的度数。已知:AB∥CD。试探索
①∠A、∠C与∠AEC之间的关系;
②∠B、∠D与∠BFD之间的关系。几 何
之 旅
