5。3。1平行线的性质1[下学期]
文档属性
| 名称 | 5。3。1平行线的性质1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-05 19:11:00 | ||
图片预览







文档简介
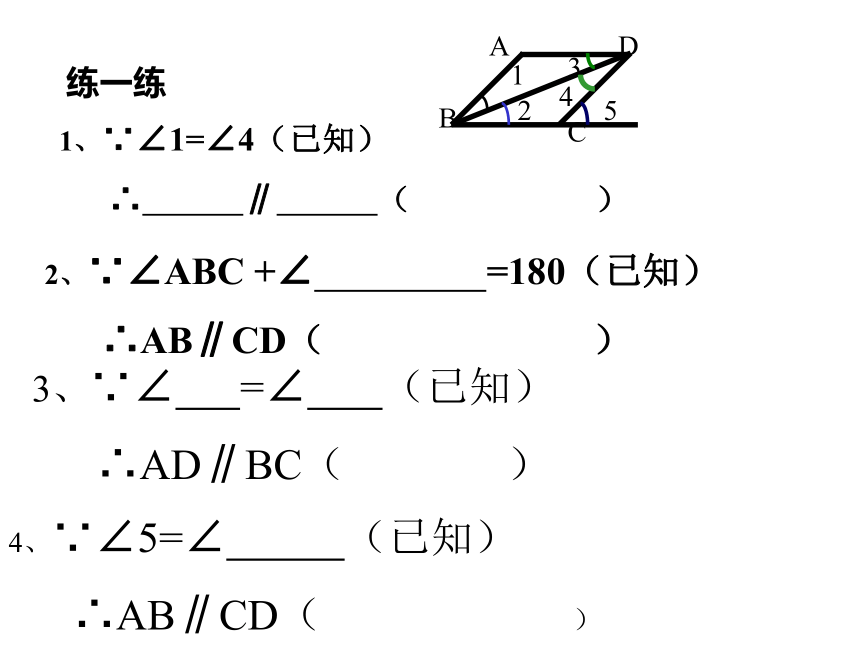
课件50张PPT。5.3.1平行线的性质(1)平行线的判定1.同位角相等,两直线平行2.内错角相等,两直线平行3.同旁内角互补,两直线平行练一练1、∵∠1=∠4(已知)
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
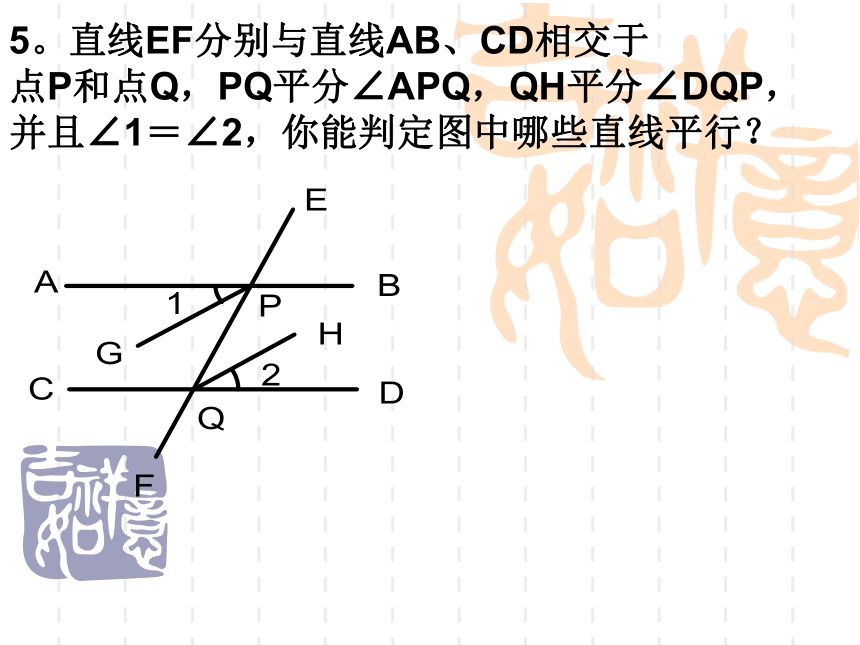
∴AB∥CD( )5。直线EF分别与直线AB、CD相交于
点P和点Q,PQ平分∠APQ,QH平分∠DQP,
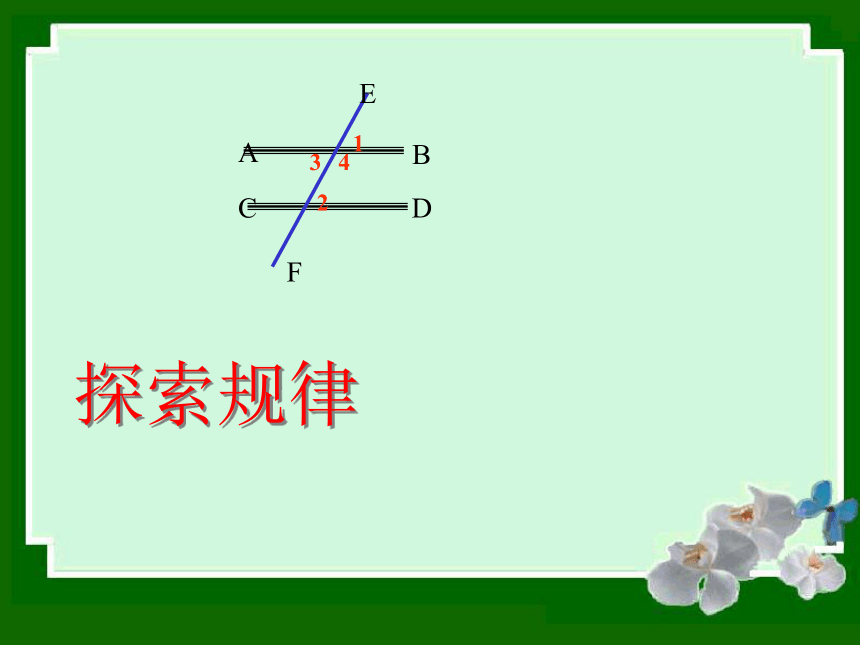
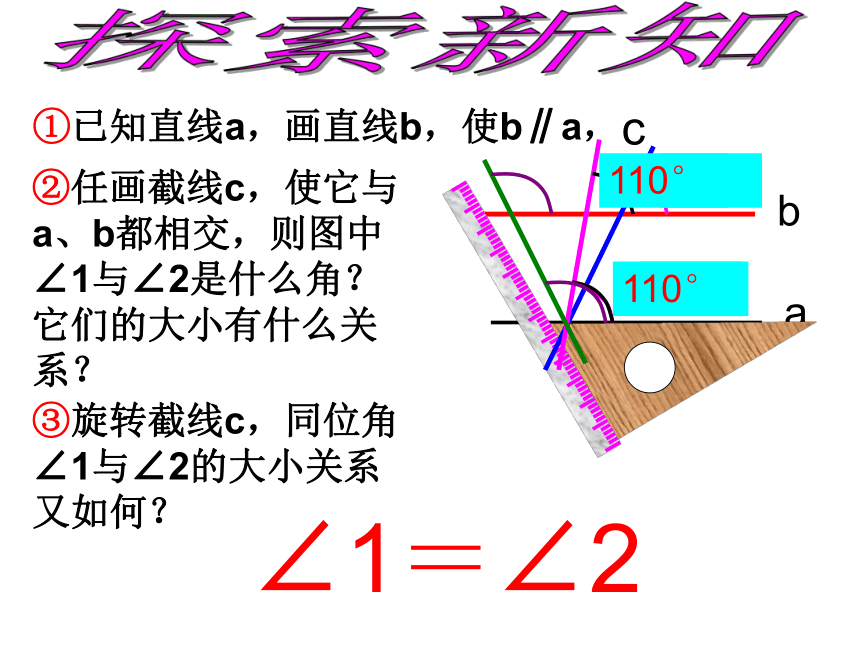
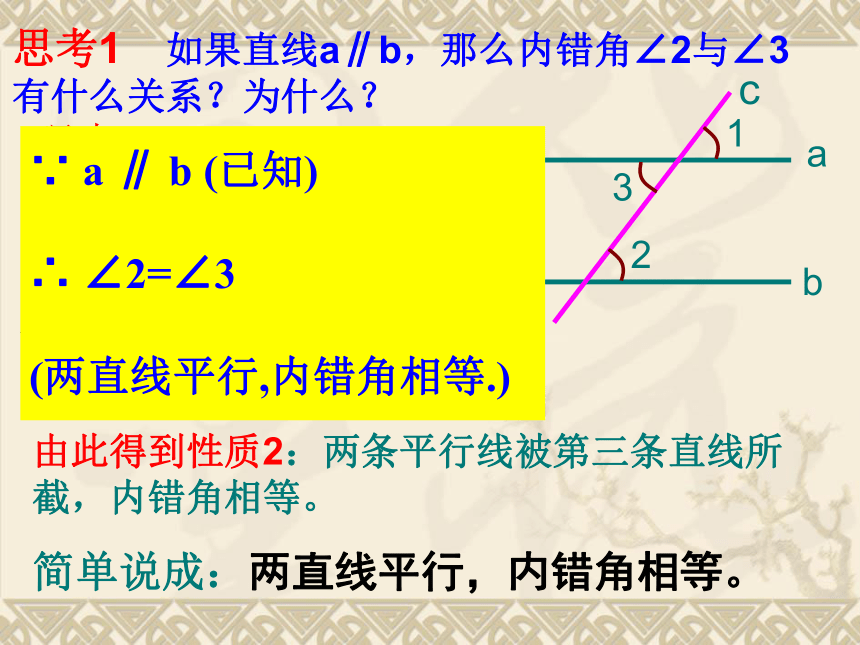
并且∠1=∠2,你能判定图中哪些直线平行? 疑问解答:.如果已知两条直线平行,你知道同位角之间有什么关系呢?内错角,同旁内角之间又有什么关系呢?探索规律探索新知①已知直线a,画直线b,使b∥a,ab②任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?1258°58°82°82°110°110°③旋转截线c,同位角∠1与∠2的大小关系又如何?∠1=∠2c通过上面的实验测量,可以得到性质1:两条平行线被第三条直线所截,同位角相等。12ab∠1=∠2简单说成:两直线平行,同位角相等cabc123思考1 如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?理由:∵a∥b(已知)∴∠1 = ∠2
(两直线平行,同位角相等)又∵ ∠1 = ∠3 ∴ ∠2 = ∠3由此得到性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。(对顶角相等)(等量代换)∵ a ∥ b (已知)
∴ ∠2=∠3
(两直线平行,内错角相等.)abc1234思考2 如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?理由:方法1:∵a∥b(已知)∴∠1 = ∠2
(两直线平行,同位角相等)又∵ ∠1 + ∠4=180°∴∠2 +∠4=180°(等量代换)由此得到性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。(邻补角定义)方法2:∵a∥b(已知)∴∠2=∠3(两直线平行,内错角相等)又∵∠3+∠4=180°(邻补角定义)∴∠2+∠4=180°(等量代换)∵ a ∥ b (已知)
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补.)平行线的性质1
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。 精彩回放实践是检验真理的唯一标准加油!归纳:1.两条平行线被第三条直线所截,同位角相等.归纳:2.两条平行线被第三条直线所截,内错角相等.归纳:3.两条平行线被第三条直线所截,同旁内角互补.知识应用:完成并比较.如图,
(1)∵a∥b(已知),
∴∠1___∠2(? ? )
(2)∵? a∥b? (已知),
∴∠2___∠3( ? )
(3)∵a∥b(已知),
∴∠2+∠4=____( ?? )= 两直线平行,同位角相等= 两直线平行,内错角相等 180°两直线平行,同旁内角互补同位角相等
内错角相等
同旁内角互补两直线平行判定性质已知结论结论已知平行线的性质与判定的区别:练习1.如图,a∥b,∠1=140o,则∠2=_____,∠3=______,∠4=______140o40o40o2.如图,
如果AD∥BC,那么根据两直线平行,同旁内角互补,
可得∠____+∠ABC=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,
可得∠____+∠ABC=180°.
DABBCD3.如图,已知∠1=100o,∠2=80o,∠3=105o,则∠4=_______105oabcd4、如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?如图,已知:∠1=∠2,∠1=∠B, 求证:AB∥EF,DE∥BC。 证明:由∠1=∠2 (已知),
根据: .
得AB∥EF.
又由∠1=∠B( ).
根据:同位角相等,两直线平行
得 ∥ .
内错角相等,两直线平行已知DE BC如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E. 证明:由 (已知), 根据:两直线平行,内错角相等 得:∠ABD= . 由AE∥BD( ). 根据: . 得∠BDC=∠E .
再根据:等量代换 得: = .AB∥CD∠ BDC已知两直线平行,同位角相等∠ ABD ∠E生活数学1: 如图某玻璃碎片是梯形,已有上底的一部分,量得∠A=115°,∠D=100°,梯形另外两个角各是多少度?
解:∵AD∥BC (已知)
∴? A +? B=180°
(两直线平行,同旁内角互补)
即 ∠B= 180°-? A=180°-115°=65°
∵AD∥BC (已知)
∴? D+ ? C=180°
(两直线平行,同旁内角互补)
即? C=180°-? D =180°-100°=80°
答:梯形的另外两个角分别为65°、80° 。引例1 小明必须要订做一块与原来一模一样的新玻璃,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度时,才能为小明合理地解决问题。如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
分析:将实际问题转换为数学问题
已知: AB ∥ CD, ∠B= 142°
求: ∠C=?生活数学2: 练习1 一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?BCAD解∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠C=∠B=142°(已知)(等量代换)练习2 判断正误
①两直线被第三条直线所截,同位角相等。( )
②两直线平行,同旁内角相等。( )
③“内错角相等,两直线平行”是平行线的性质。( )
④“两直线平行,同旁内角互补”是平行线的性质。( )×√××生活中的数学:一束平行光线AB与DE射向一个水平镜面后被反射,此时:1) ∠1、∠3大小 有什么关系?
2)你能找去其他相等的角吗?
3)反射光线BC与EF也平行吗?平行线的判定1.同位角相等,两直线平行2.内错角相等,两直线平行3.同旁内角互补,两直线平行两条平行线被第三条直线所
截,同位角相等.简单说成:
两直线平行,同位角相等两条平行线被第三条直线所截,
同旁内角互补,简单说成:
两直线平行,同旁内角互补两条平行线被第三条直线所 截,内错角相等.简单说成:两直线平行,同位角相等平行线的性质感悟模式∵DE∥BC∴DE∥BC建模应用小结next引入.如图,直线a//b,∠1=54o,那么∠2,∠3,∠4各是多少度?为什么?∠1= ∠3,___//__ECBDAFG165432∠4= ∠E,___//__∠6= ∠C,___//__∠2= ____,AD//BE如图,已知:∠1+∠2=180°, 求证:AB∥CD.证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4( ) 根据:等量代换 得:∠3+ =180°.
根据:同旁内角互补,两直线平行
得: ∥ .对顶角相等∠4AB CD如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD. 证明:由AC∥DE (已知), 根据:两直线平行,内错角相等. 得∠ACD= .
又由∠1=∠2(已知). 根据: . 得∠1=∠ACD . 再根据: . 得 ∥ .∠ 2等量代换内错角相等,两直线平行AB CD如图,已知:∠DAF=∠AFE,∠ADC+∠DCB=180°,求证:EF∥BC证明:由:∠DAF=∠AFE ( )
根据: .
得:AD∥ .
由:∠ADC+ =180°(已知). 根据: .
得:AD∥ .
再根据: .
得:EF∥BC已知内错角相等,两直线平行EF∠DCB同旁内角互补,两直线平行BC平行于同一直线的两条直线互相平行.如图,已知:AB∥CD,∠A=70°∠DHE=70°,求证:AM∥EF已知:如图,直线 a∥b,c∥d,∠1=100°,求 :∠2,∠3的度数.解(1)因为? c∥d,(已知)
所以? ∠1=∠4.( )
又因为? ∠3=∠4,( )
所以 ?∠1=∠3,(等量代换)
因为? ∠1=100°,(已知)
所以? ∠3= .(等量代换)
(2)因为? a∥b,(已知)
所以? ∠2+∠4=180°.( )
所以? ∠2= .两直线平行,同位角相等对顶角相等 100°两直线平行,同旁内角互补180°- 100°= 80° 已知,如图AB∥EF∥CD,AC∥BD,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D建模应用小结next引入AB//CD//PN, ∠ABC=500 ∠CPN=1500 ∠BCP=______.CBDANP如图:AC//BD, ∠EBD=400 ∠EBD=700 ∠AEB=______DEBCA4007001.两点间的距离-----连接两点的线段的长度.2.点到直线的距离-----直线外一点到这条直线 的垂线段的长度.画一个5×5的方格探究(1)用三角尺和直尺画平行线,做成一张5X5个格子的方格纸(2)观察自己画的方格纸并说说特点(3)思考:图中两条平行线之间的线段都与平行线垂直吗?它们的长度都相等吗?归纳:同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度叫做这两条平行线间的距离.两条平行线之间距离.如图,两条平行线中,一条直线上的点到另一条直线的距离处处相等.
叫做
pMab即:线段PM的长度叫平行线a与b之间的距离温馨提醒:不是垂线段本身, 而 是垂线段的长度
如图a∥b,AB⊥a于A,CD⊥b于C,
1)点B与点D的距离是指线段 的长;
2)点D到直线b的距离是指 ;
3)两平行线a,b的距离是 或 ;
4)线段AB的长可指 的距离.考考你baABcD1.两点间的距离-----连接两点的线段的长度.2.点到直线的距离-----直线外一点到这条直的垂线段的长度.三种距离的定义: -----两条平行线中,一条直线上的点到另一条
直线的垂线段的长度
3.两平行线间的距离
再见
∴ ∥ ( )2、∵∠ABC +∠ =180(已知)
∴AB∥CD( )3、∵∠ =∠ (已知)
∴AD∥BC( )4、∵∠5=∠ (已知)
∴AB∥CD( )5。直线EF分别与直线AB、CD相交于
点P和点Q,PQ平分∠APQ,QH平分∠DQP,
并且∠1=∠2,你能判定图中哪些直线平行? 疑问解答:.如果已知两条直线平行,你知道同位角之间有什么关系呢?内错角,同旁内角之间又有什么关系呢?探索规律探索新知①已知直线a,画直线b,使b∥a,ab②任画截线c,使它与a、b都相交,则图中∠1与∠2是什么角?它们的大小有什么关系?1258°58°82°82°110°110°③旋转截线c,同位角∠1与∠2的大小关系又如何?∠1=∠2c通过上面的实验测量,可以得到性质1:两条平行线被第三条直线所截,同位角相等。12ab∠1=∠2简单说成:两直线平行,同位角相等cabc123思考1 如果直线a∥b,那么内错角∠2与∠3有什么关系?为什么?理由:∵a∥b(已知)∴∠1 = ∠2
(两直线平行,同位角相等)又∵ ∠1 = ∠3 ∴ ∠2 = ∠3由此得到性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。(对顶角相等)(等量代换)∵ a ∥ b (已知)
∴ ∠2=∠3
(两直线平行,内错角相等.)abc1234思考2 如果直线a∥b,那么同旁内角∠2与∠4有什么关系?为什么?理由:方法1:∵a∥b(已知)∴∠1 = ∠2
(两直线平行,同位角相等)又∵ ∠1 + ∠4=180°∴∠2 +∠4=180°(等量代换)由此得到性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。(邻补角定义)方法2:∵a∥b(已知)∴∠2=∠3(两直线平行,内错角相等)又∵∠3+∠4=180°(邻补角定义)∴∠2+∠4=180°(等量代换)∵ a ∥ b (已知)
∴ ∠2+∠4=180°
(两直线平行,同旁内角互补.)平行线的性质1
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。 精彩回放实践是检验真理的唯一标准加油!归纳:1.两条平行线被第三条直线所截,同位角相等.归纳:2.两条平行线被第三条直线所截,内错角相等.归纳:3.两条平行线被第三条直线所截,同旁内角互补.知识应用:完成并比较.如图,
(1)∵a∥b(已知),
∴∠1___∠2(? ? )
(2)∵? a∥b? (已知),
∴∠2___∠3( ? )
(3)∵a∥b(已知),
∴∠2+∠4=____( ?? )= 两直线平行,同位角相等= 两直线平行,内错角相等 180°两直线平行,同旁内角互补同位角相等
内错角相等
同旁内角互补两直线平行判定性质已知结论结论已知平行线的性质与判定的区别:练习1.如图,a∥b,∠1=140o,则∠2=_____,∠3=______,∠4=______140o40o40o2.如图,
如果AD∥BC,那么根据两直线平行,同旁内角互补,
可得∠____+∠ABC=180°;
(2)如果AB∥CD,那么根据两直线平行,同旁内角互补,
可得∠____+∠ABC=180°.
DABBCD3.如图,已知∠1=100o,∠2=80o,∠3=105o,则∠4=_______105oabcd4、如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?如图,已知:∠1=∠2,∠1=∠B, 求证:AB∥EF,DE∥BC。 证明:由∠1=∠2 (已知),
根据: .
得AB∥EF.
又由∠1=∠B( ).
根据:同位角相等,两直线平行
得 ∥ .
内错角相等,两直线平行已知DE BC如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E. 证明:由 (已知), 根据:两直线平行,内错角相等 得:∠ABD= . 由AE∥BD( ). 根据: . 得∠BDC=∠E .
再根据:等量代换 得: = .AB∥CD∠ BDC已知两直线平行,同位角相等∠ ABD ∠E生活数学1: 如图某玻璃碎片是梯形,已有上底的一部分,量得∠A=115°,∠D=100°,梯形另外两个角各是多少度?
解:∵AD∥BC (已知)
∴? A +? B=180°
(两直线平行,同旁内角互补)
即 ∠B= 180°-? A=180°-115°=65°
∵AD∥BC (已知)
∴? D+ ? C=180°
(两直线平行,同旁内角互补)
即? C=180°-? D =180°-100°=80°
答:梯形的另外两个角分别为65°、80° 。引例1 小明必须要订做一块与原来一模一样的新玻璃,已知量得∠A=115°,∠D=100°,请你想一想,梯形的另外两个角各是多少度时,才能为小明合理地解决问题。如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142°,第二次拐的角∠C是多少度?
分析:将实际问题转换为数学问题
已知: AB ∥ CD, ∠B= 142°
求: ∠C=?生活数学2: 练习1 一自行车运动员在一条公路上骑车,两次拐弯后,和原来的方向相同(即拐弯前后的两条路互相平行),若测得第一次拐弯的∠B是142°,则第二次拐弯的∠C应是多少度才合理?为什么?BCAD解∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠C=∠B=142°(已知)(等量代换)练习2 判断正误
①两直线被第三条直线所截,同位角相等。( )
②两直线平行,同旁内角相等。( )
③“内错角相等,两直线平行”是平行线的性质。( )
④“两直线平行,同旁内角互补”是平行线的性质。( )×√××生活中的数学:一束平行光线AB与DE射向一个水平镜面后被反射,此时:1) ∠1、∠3大小 有什么关系?
2)你能找去其他相等的角吗?
3)反射光线BC与EF也平行吗?平行线的判定1.同位角相等,两直线平行2.内错角相等,两直线平行3.同旁内角互补,两直线平行两条平行线被第三条直线所
截,同位角相等.简单说成:
两直线平行,同位角相等两条平行线被第三条直线所截,
同旁内角互补,简单说成:
两直线平行,同旁内角互补两条平行线被第三条直线所 截,内错角相等.简单说成:两直线平行,同位角相等平行线的性质感悟模式∵DE∥BC∴DE∥BC建模应用小结next引入.如图,直线a//b,∠1=54o,那么∠2,∠3,∠4各是多少度?为什么?∠1= ∠3,___//__ECBDAFG165432∠4= ∠E,___//__∠6= ∠C,___//__∠2= ____,AD//BE如图,已知:∠1+∠2=180°, 求证:AB∥CD.证明:由:∠1+∠2=180°(已知),
∠1=∠3(对顶角相等).
∠2=∠4( ) 根据:等量代换 得:∠3+ =180°.
根据:同旁内角互补,两直线平行
得: ∥ .对顶角相等∠4AB CD如图,已知:AC∥DE,∠1=∠2,试说明AB∥CD. 证明:由AC∥DE (已知), 根据:两直线平行,内错角相等. 得∠ACD= .
又由∠1=∠2(已知). 根据: . 得∠1=∠ACD . 再根据: . 得 ∥ .∠ 2等量代换内错角相等,两直线平行AB CD如图,已知:∠DAF=∠AFE,∠ADC+∠DCB=180°,求证:EF∥BC证明:由:∠DAF=∠AFE ( )
根据: .
得:AD∥ .
由:∠ADC+ =180°(已知). 根据: .
得:AD∥ .
再根据: .
得:EF∥BC已知内错角相等,两直线平行EF∠DCB同旁内角互补,两直线平行BC平行于同一直线的两条直线互相平行.如图,已知:AB∥CD,∠A=70°∠DHE=70°,求证:AM∥EF已知:如图,直线 a∥b,c∥d,∠1=100°,求 :∠2,∠3的度数.解(1)因为? c∥d,(已知)
所以? ∠1=∠4.( )
又因为? ∠3=∠4,( )
所以 ?∠1=∠3,(等量代换)
因为? ∠1=100°,(已知)
所以? ∠3= .(等量代换)
(2)因为? a∥b,(已知)
所以? ∠2+∠4=180°.( )
所以? ∠2= .两直线平行,同位角相等对顶角相等 100°两直线平行,同旁内角互补180°- 100°= 80° 已知,如图AB∥EF∥CD,AC∥BD,BC平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D建模应用小结next引入AB//CD//PN, ∠ABC=500 ∠CPN=1500 ∠BCP=______.CBDANP如图:AC//BD, ∠EBD=400 ∠EBD=700 ∠AEB=______DEBCA4007001.两点间的距离-----连接两点的线段的长度.2.点到直线的距离-----直线外一点到这条直线 的垂线段的长度.画一个5×5的方格探究(1)用三角尺和直尺画平行线,做成一张5X5个格子的方格纸(2)观察自己画的方格纸并说说特点(3)思考:图中两条平行线之间的线段都与平行线垂直吗?它们的长度都相等吗?归纳:同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度叫做这两条平行线间的距离.两条平行线之间距离.如图,两条平行线中,一条直线上的点到另一条直线的距离处处相等.
叫做
pMab即:线段PM的长度叫平行线a与b之间的距离温馨提醒:不是垂线段本身, 而 是垂线段的长度
如图a∥b,AB⊥a于A,CD⊥b于C,
1)点B与点D的距离是指线段 的长;
2)点D到直线b的距离是指 ;
3)两平行线a,b的距离是 或 ;
4)线段AB的长可指 的距离.考考你baABcD1.两点间的距离-----连接两点的线段的长度.2.点到直线的距离-----直线外一点到这条直的垂线段的长度.三种距离的定义: -----两条平行线中,一条直线上的点到另一条
直线的垂线段的长度
3.两平行线间的距离
再见
