5.3平行线的性质[下学期]
文档属性
| 名称 | 5.3平行线的性质[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-06 08:29:00 | ||
图片预览





文档简介
课件20张PPT。5.3平行线的性质北师大七年级(下)知识回顾:(1)因为∠1_____∠ 2( 已知),
所以 a∥b
(2)因为∠2_____∠3 (已知),
所以 a∥b
(3)因为∠4+∠2= _____ (已知),
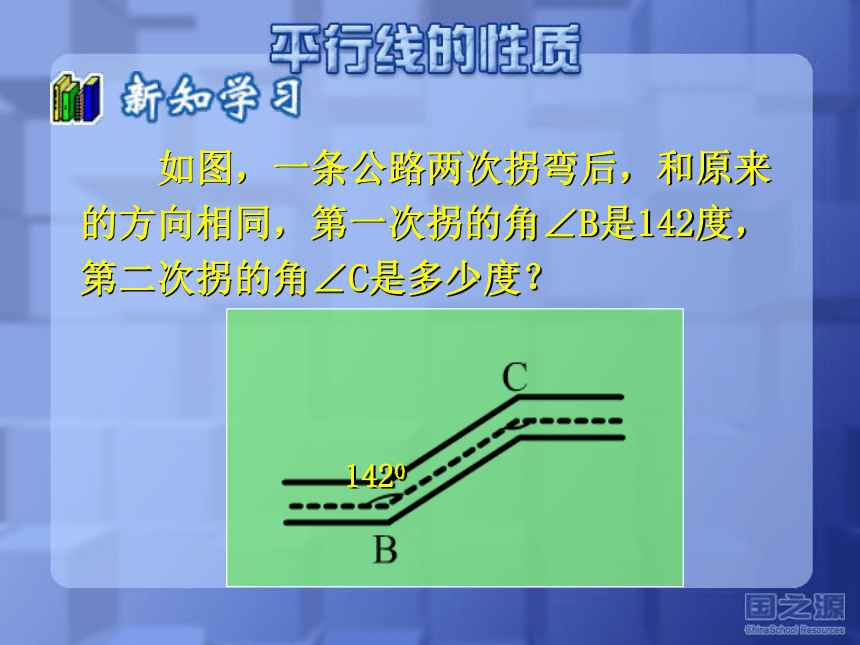
所以 a∥b==1800(内错角相等,两直线平行)(同位角相等,两直线平行)(同旁内角互补,两直线平行) 如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142度,第二次拐的角∠C是多少度?1420? 两条平行线被第三条直线所截,同位角有什么关系呢?
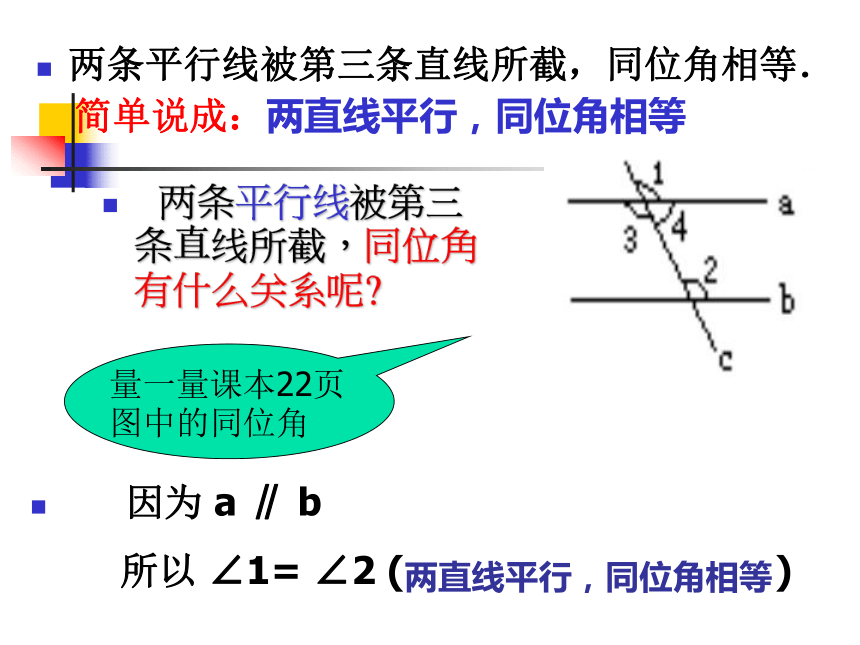
因为 a ∥ b
所以 ∠1= ∠2 ( ?? )两直线平行,同位角相等量一量课本22页图中的同位角两条平行线被第三条直线所截,同位角相等.
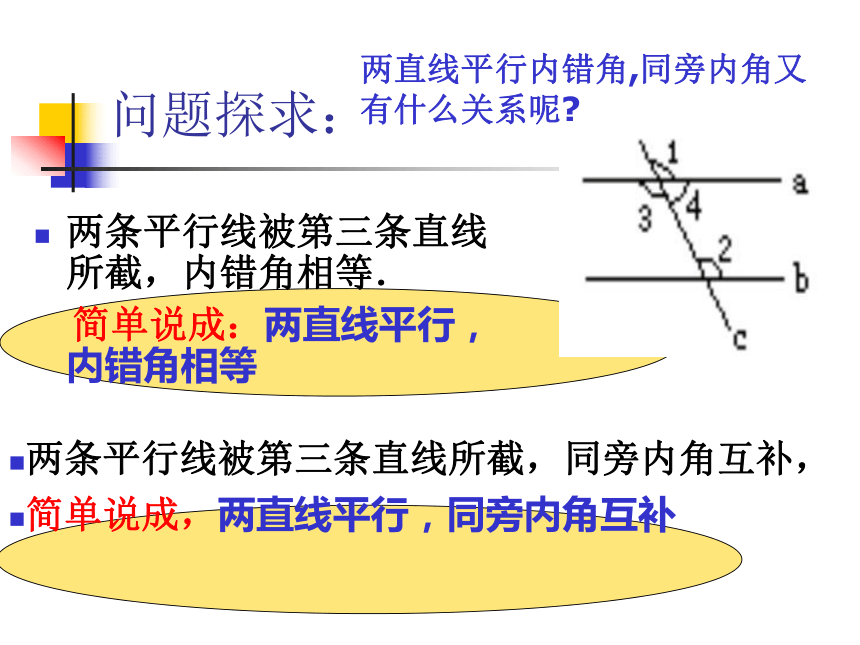
简单说成:两直线平行,同位角相等两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等两条平行线被第三条直线所截,同旁内角互补,
简单说成,两直线平行,同旁内角互补问题探求:两直线平行内错角,同旁内角又有什么关系呢?22页思考题目如图:已知平行线AB、CD被直线AE所截
(1)从∠1=110°,可以知 道∠2是多少度?为什么?(2)从∠1=110°,可以知道∠3是多少度? 为什么?
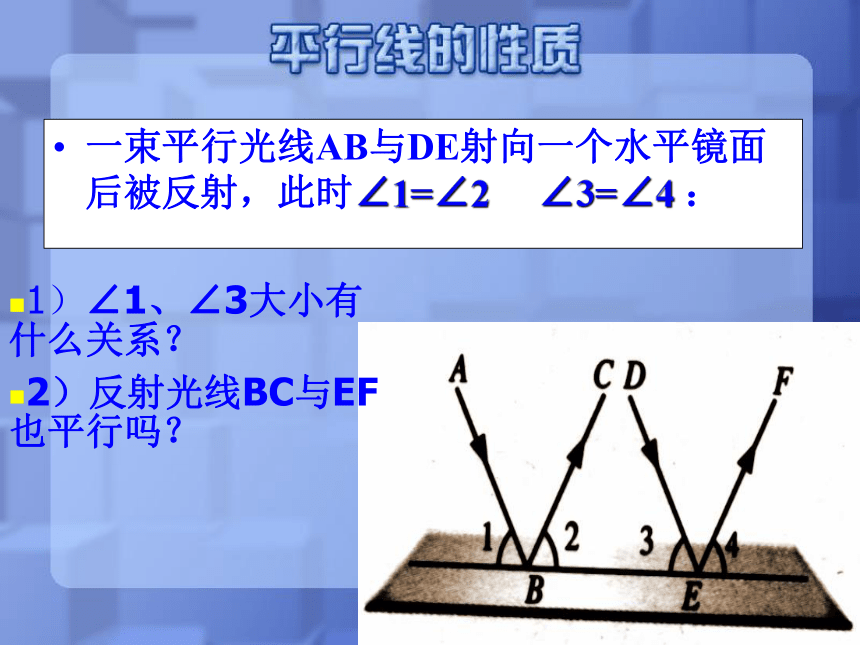
(3)从∠1=110°,可以知道∠4是多少度, 为什么?一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2 ∠3=∠4 :1)∠1、∠3大小有什么关系?
2)反射光线BC与EF也平行吗?例1:如下图,a∥b∥c,直线l与a、b、c相交,那么与∠α相等的角有:( )A.2个 B.3个 C.4个 D.5个分析:本题中有1个对顶角、
2个同位角、1个内错
角、1个外错角。D例2:如图,是梯形有上底的一部分,已经量
得∠A=115°,∠D=100°,梯形另外
两个角各是多少度?解:因为梯形上下底互相平行所以∠A与∠B互补,
∠D与∠C互补于是
∠B=180°-115°=65°∠C=180°-100°=80°23页探究题目 同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离。如图,如果 AB∥CD,在CD上任取一点E,向AB作垂线段EF,这时,EF是否也垂直于直线CD呢?我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗?BD判断一件事情的语句,叫做命题。命题由 题设 和 结论 两部分构成。题设 是已知事项;结论 是由已知事项推出的事项。命题还可以写成 “如果……那么……”的形式。分析下列命题:1、如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
2、等式两边加同一个数,结果仍是等式;
3、对顶角相等。 判断以下语句是否是命题,如果是请找出它的题设和结论部分。1、画线段 AB=CD;
2、等式两边同成一个数,结果仍是等式;
3、两直线平行,内错角相等。以上命题是正确的吗?
命题“如果两个角互补,那么它们是邻补角”是正确的吗? 如果题设成立,那么结论一定成立,这样的命题,叫做真命题。 命题真命题:假命题: 如果题设成立时,结论不成立,这样的命题都是错误的命题,叫做假命题。命题的分类:命题是一个判断,判断的结果就有对错之分。因此就要引入真假命题,判断真、假命题的大前提,首先是命题。如:“延长直线AB”,这本身不是命题,也不是真、假命题。 练习5:下列语句是命题吗?若是请将它改写成 “如果…那么…”的形式,并判断其真假: 3.等式两边加上同一个数或同一个整式, 所得的结果仍是等式。2.两个角的和等于平角时, 这两个角互补。 1.两条平行线被第三条直线所截, 同旁内角互补 。 如果如果如果那么那么那么4. 用直尺画一条线段.(是)(是)(是)(不是)(真命题)(真命题)(真命题)6.任意两个直角都相等。 5.平行于同一条直线的两条直线平行。如果两条直线平行于同一条直线,那么这两条直线也互相平行。如果两个角是直角,那么这两个角相等。(是)(是)7. 同位角相等.(是)如果两个角是同位角,那么这两个角相等.(真命题)(真命题)(假命题)1.命题及命题的构成。小结:2.命题形式的改写。3.命题的分类及判断真假命题的方法。判断一件事情的句子,叫做命题。命题=题设+结论。如果+题设,那么+结论。
所以 a∥b
(2)因为∠2_____∠3 (已知),
所以 a∥b
(3)因为∠4+∠2= _____ (已知),
所以 a∥b==1800(内错角相等,两直线平行)(同位角相等,两直线平行)(同旁内角互补,两直线平行) 如图,一条公路两次拐弯后,和原来的方向相同,第一次拐的角∠B是142度,第二次拐的角∠C是多少度?1420? 两条平行线被第三条直线所截,同位角有什么关系呢?
因为 a ∥ b
所以 ∠1= ∠2 ( ?? )两直线平行,同位角相等量一量课本22页图中的同位角两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等两条平行线被第三条直线所截,同旁内角互补,
简单说成,两直线平行,同旁内角互补问题探求:两直线平行内错角,同旁内角又有什么关系呢?22页思考题目如图:已知平行线AB、CD被直线AE所截
(1)从∠1=110°,可以知 道∠2是多少度?为什么?(2)从∠1=110°,可以知道∠3是多少度? 为什么?
(3)从∠1=110°,可以知道∠4是多少度, 为什么?一束平行光线AB与DE射向一个水平镜面后被反射,此时∠1=∠2 ∠3=∠4 :1)∠1、∠3大小有什么关系?
2)反射光线BC与EF也平行吗?例1:如下图,a∥b∥c,直线l与a、b、c相交,那么与∠α相等的角有:( )A.2个 B.3个 C.4个 D.5个分析:本题中有1个对顶角、
2个同位角、1个内错
角、1个外错角。D例2:如图,是梯形有上底的一部分,已经量
得∠A=115°,∠D=100°,梯形另外
两个角各是多少度?解:因为梯形上下底互相平行所以∠A与∠B互补,
∠D与∠C互补于是
∠B=180°-115°=65°∠C=180°-100°=80°23页探究题目 同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离。如图,如果 AB∥CD,在CD上任取一点E,向AB作垂线段EF,这时,EF是否也垂直于直线CD呢?我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗?BD判断一件事情的语句,叫做命题。命题由 题设 和 结论 两部分构成。题设 是已知事项;结论 是由已知事项推出的事项。命题还可以写成 “如果……那么……”的形式。分析下列命题:1、如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
2、等式两边加同一个数,结果仍是等式;
3、对顶角相等。 判断以下语句是否是命题,如果是请找出它的题设和结论部分。1、画线段 AB=CD;
2、等式两边同成一个数,结果仍是等式;
3、两直线平行,内错角相等。以上命题是正确的吗?
命题“如果两个角互补,那么它们是邻补角”是正确的吗? 如果题设成立,那么结论一定成立,这样的命题,叫做真命题。 命题真命题:假命题: 如果题设成立时,结论不成立,这样的命题都是错误的命题,叫做假命题。命题的分类:命题是一个判断,判断的结果就有对错之分。因此就要引入真假命题,判断真、假命题的大前提,首先是命题。如:“延长直线AB”,这本身不是命题,也不是真、假命题。 练习5:下列语句是命题吗?若是请将它改写成 “如果…那么…”的形式,并判断其真假: 3.等式两边加上同一个数或同一个整式, 所得的结果仍是等式。2.两个角的和等于平角时, 这两个角互补。 1.两条平行线被第三条直线所截, 同旁内角互补 。 如果如果如果那么那么那么4. 用直尺画一条线段.(是)(是)(是)(不是)(真命题)(真命题)(真命题)6.任意两个直角都相等。 5.平行于同一条直线的两条直线平行。如果两条直线平行于同一条直线,那么这两条直线也互相平行。如果两个角是直角,那么这两个角相等。(是)(是)7. 同位角相等.(是)如果两个角是同位角,那么这两个角相等.(真命题)(真命题)(假命题)1.命题及命题的构成。小结:2.命题形式的改写。3.命题的分类及判断真假命题的方法。判断一件事情的句子,叫做命题。命题=题设+结论。如果+题设,那么+结论。
