平行线的性质[下学期]
图片预览


文档简介
课件15张PPT。 平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
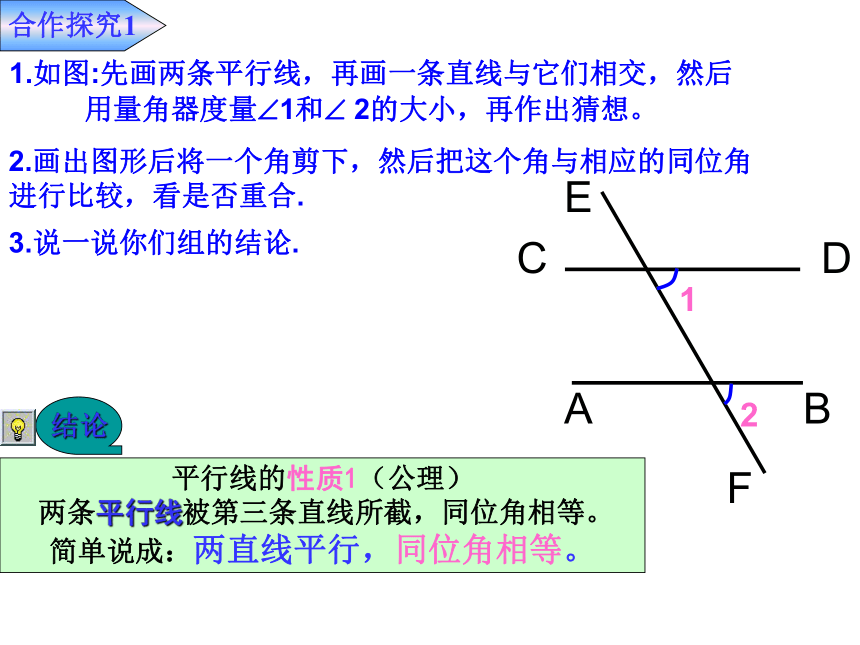
同旁内角互补两直线平行问题合作探究11.如图:先画两条平行线,再画一条直线与它们相交,然后
用量角器度量?1和? 2的大小,再作出猜想。 2.画出图形后将一个角剪下,然后把这个角与相应的同位角
进行比较,看是否重合. 3.说一说你们组的结论.平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
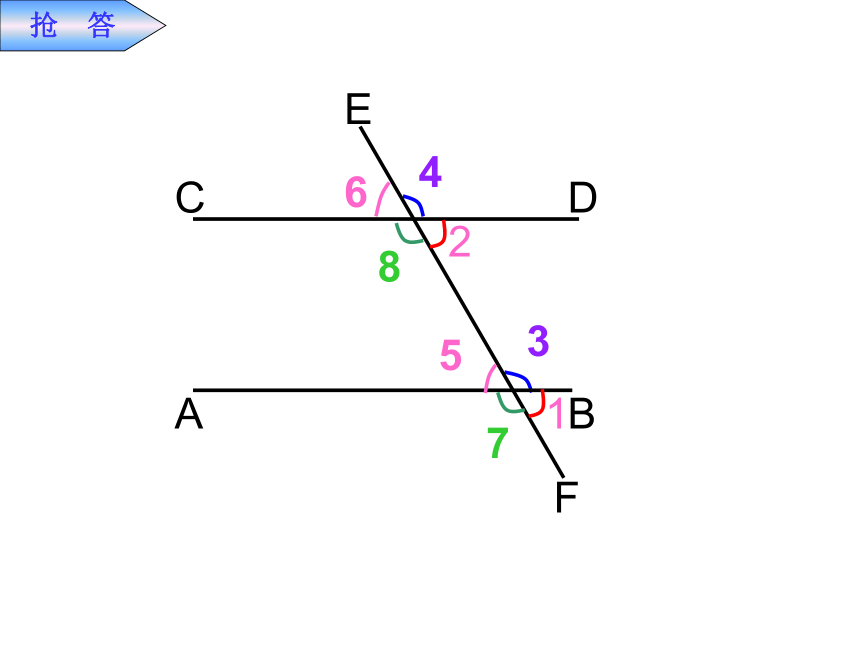
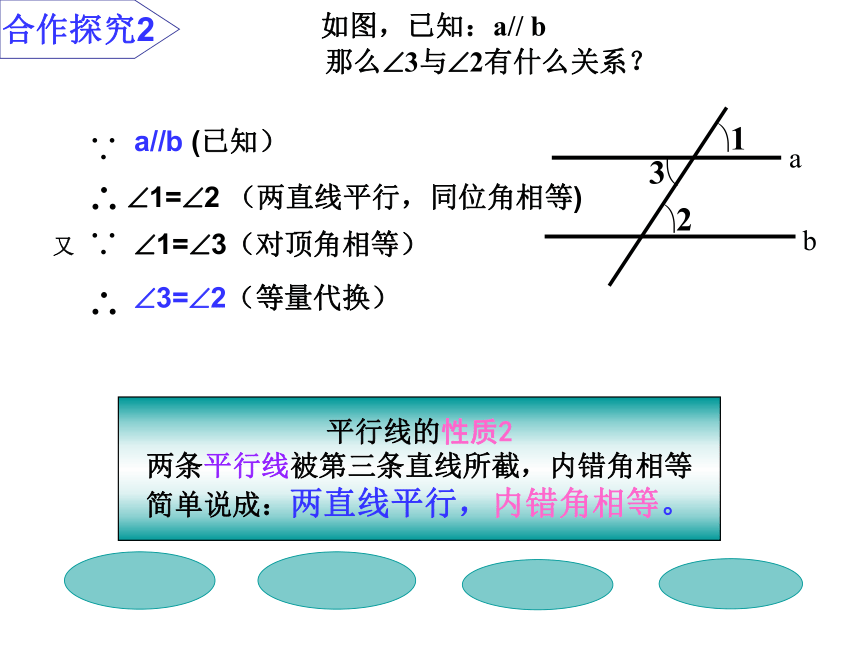
简单说成:两直线平行,同位角相等。抢 答?1?23?ab合作探究2??如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
a//b (已知)
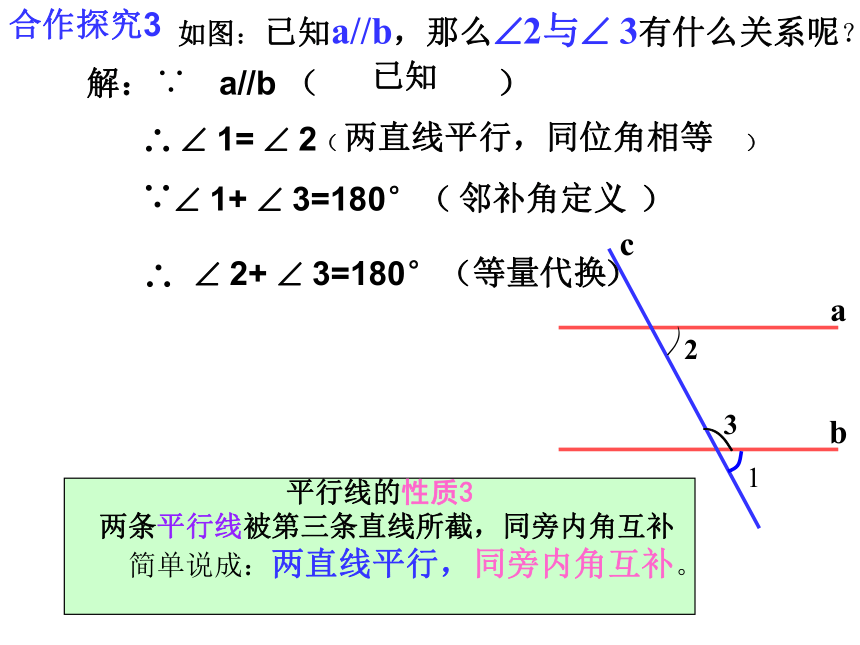
?1=?2 (两直线平行,同位角相等)c? 2?31ba 如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
等量代换 邻补角定义 已知两直线平行,同位角相等合作探究3平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
即 ? B= 180 °- ? A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结解答:∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠B=∠C=142°(已知)(等量代换)P.86EX.1(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.86EX.2 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???填空:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)又∵∠ADE =∠B (已证)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °解答:P.86EX.3同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结再见
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题合作探究11.如图:先画两条平行线,再画一条直线与它们相交,然后
用量角器度量?1和? 2的大小,再作出猜想。 2.画出图形后将一个角剪下,然后把这个角与相应的同位角
进行比较,看是否重合. 3.说一说你们组的结论.平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。抢 答?1?23?ab合作探究2??如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
a//b (已知)
?1=?2 (两直线平行,同位角相等)c? 2?31ba 如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
等量代换 邻补角定义 已知两直线平行,同位角相等合作探究3平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
即 ? B= 180 °- ? A =180 ° -115 ° =65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结解答:∵AB∥CD(已知)∴∠B=∠C(两直线平行,内错角相等)又∵∠B=142°∴∠B=∠C=142°(已知)(等量代换)P.86EX.1(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.86EX.2 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD//
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???填空:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)又∵∠ADE =∠B (已证)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °解答:P.86EX.3同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结复习回顾新课学习巩固练习课堂小结再见
