平行线的性质[下学期]
图片预览




文档简介
(共15张PPT)
南通市跃龙中学 胡剑
教学过程
1、问题引入
请同学们先复习一下前面所学过的平行线的判 定方法,并说出它们的已知和结论分别是什么?
想一想:如果交换它们的已知和结论,即让两直线平行,会有什么结论呢?
平行线的判定
两条直线被第三条直线所截,
⑴如果同位角相等,那么两直线平行;
⑵如果内错角相等,那么两直线平行;
⑶如果同旁内角互补,那么两直线平行.
带着这个问题,我们来看……
图1
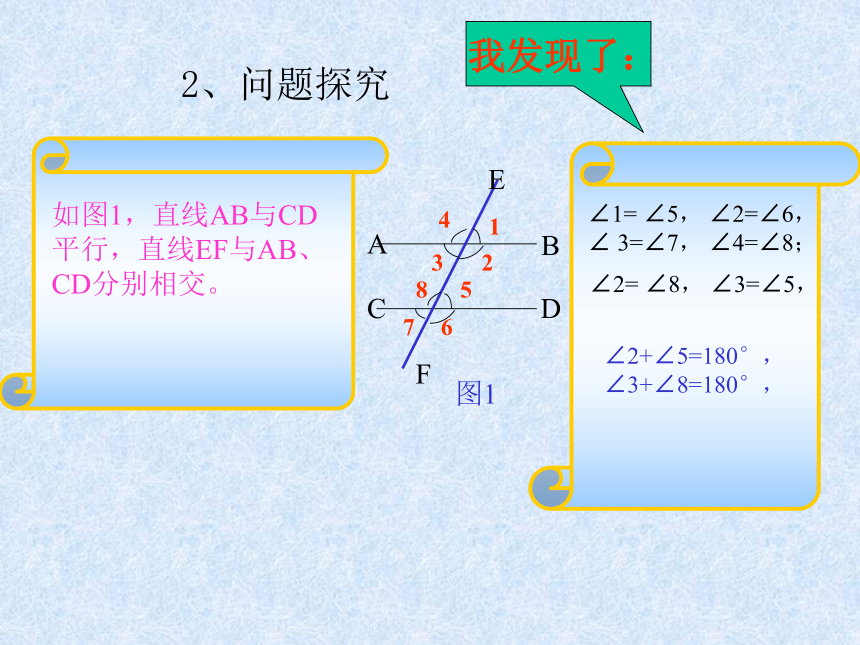
如图1,直线AB与CD平行,直线EF与AB、CD分别相交。
我发现了:
∠1= ∠5, ∠2=∠6,
∠ 3=∠7, ∠4=∠8;
∠2+∠5=180°,
∠3+∠8=180°,
∠2= ∠8, ∠3=∠5,
A
B
C
D
E
F
1
5
8
4
6
2
3
7
2、问题探究
3、归纳小结
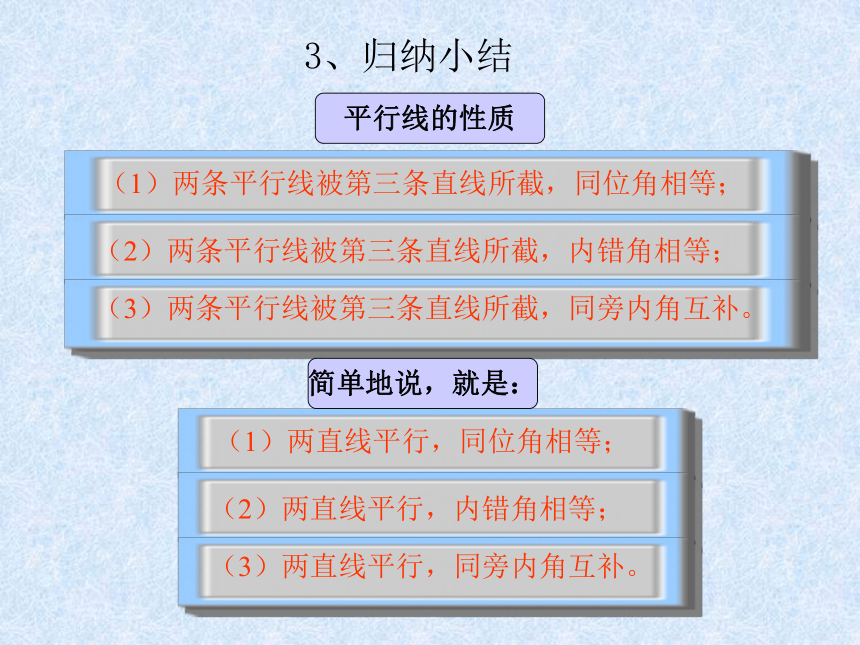
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
(1)两直线平行,同位角相等;
简单地说,就是:
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
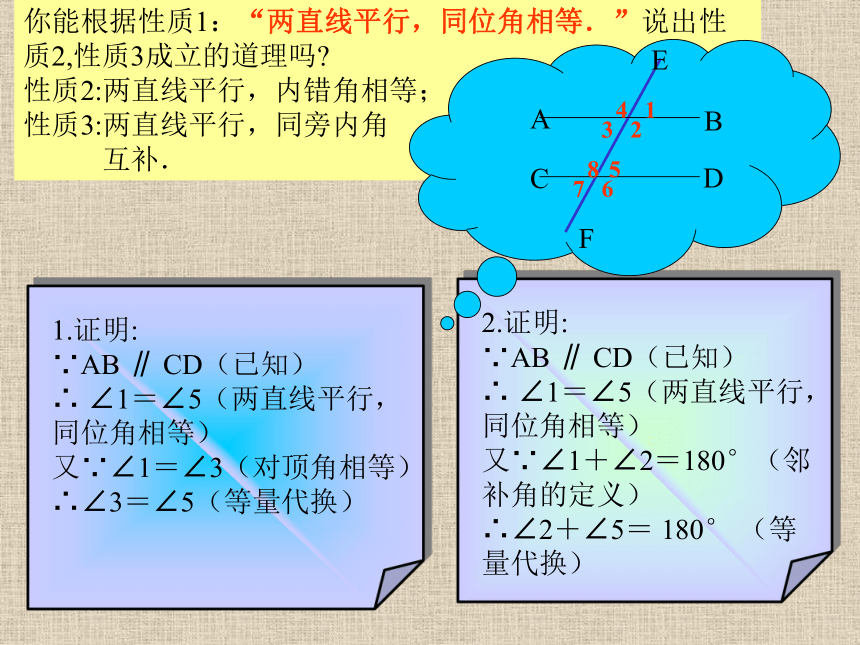
你能根据性质1:“两直线平行,同位角相等.”说出性质2,性质3成立的道理吗
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角
互补.
1.证明:
∵AB ∥ CD(已知)
∴ ∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠3(对顶角相等)
∴∠3=∠5(等量代换)
2.证明:
∵AB ∥ CD(已知)
∴ ∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠2=180°(邻补角的定义)
∴∠2+∠5= 180° (等量代换)
E
F
A
B
C
D
1
2
4
3
8
5
6
7
练习1:
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
② ∵∠1=∠B( )
∴EC∥BD( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
两直线平行,内错角相等
已知
已知
已知
已知
已知
已知
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
说明:①、②、③是平行线的判定的应用; ④、⑤、⑥是平行线的性质的应用.
4、练习
练习 2、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:∵ EF∥AD,
∴ ∠2=____(______________________)
∵ ∠1=∠2
∴ ∠1=∠3(____________)
∴ AB∥_____(_____________________)
∴∠BAC+______=180°(_____________________)
∵ ∠BAC=70°
∴ ∠AGD=_______
∠AGD
DG
∠3
110°
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,同旁内角互补
练习3:
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?
A
B
D
C
E
2
4
3
1
5、例题讲解
1、如图是梯形有上底的一部分,已经量得∠A=115°, ∠D=100°,那么梯形的另外两个角各是多少度?
2、如图,AB∥DE,BC∥EF,BC交DE于点G,∠B与∠E有什么关系?为什么?
B
A
G
E
D
C
F
3、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数 。
6、课堂小结
E
F
A
B
C
D
1
2
4
3
8
5
6
7
本节课你学到了哪些知识?
(1)平行线的性质有哪三条?
(2)如何区分平行线的判定和性质?
平行线的性质有以下三条,
(1)两直线平行,同位角相等,
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补.
由角的已知条件推出两直线平行的结论是平行线的判定;而由两直线平行的条件推出角的结论则是平行线的性质.
P25 : 4、5、6、7
南通市跃龙中学 胡剑
教学过程
1、问题引入
请同学们先复习一下前面所学过的平行线的判 定方法,并说出它们的已知和结论分别是什么?
想一想:如果交换它们的已知和结论,即让两直线平行,会有什么结论呢?
平行线的判定
两条直线被第三条直线所截,
⑴如果同位角相等,那么两直线平行;
⑵如果内错角相等,那么两直线平行;
⑶如果同旁内角互补,那么两直线平行.
带着这个问题,我们来看……
图1
如图1,直线AB与CD平行,直线EF与AB、CD分别相交。
我发现了:
∠1= ∠5, ∠2=∠6,
∠ 3=∠7, ∠4=∠8;
∠2+∠5=180°,
∠3+∠8=180°,
∠2= ∠8, ∠3=∠5,
A
B
C
D
E
F
1
5
8
4
6
2
3
7
2、问题探究
3、归纳小结
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
(1)两直线平行,同位角相等;
简单地说,就是:
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
你能根据性质1:“两直线平行,同位角相等.”说出性质2,性质3成立的道理吗
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角
互补.
1.证明:
∵AB ∥ CD(已知)
∴ ∠1=∠5(两直线平行,同位角相等)
又∵∠1=∠3(对顶角相等)
∴∠3=∠5(等量代换)
2.证明:
∵AB ∥ CD(已知)
∴ ∠1=∠5(两直线平行,同位角相等)
又∵∠1+∠2=180°(邻补角的定义)
∴∠2+∠5= 180° (等量代换)
E
F
A
B
C
D
1
2
4
3
8
5
6
7
练习1:
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
② ∵∠1=∠B( )
∴EC∥BD( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
两直线平行,内错角相等
已知
已知
已知
已知
已知
已知
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
说明:①、②、③是平行线的判定的应用; ④、⑤、⑥是平行线的性质的应用.
4、练习
练习 2、如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:∵ EF∥AD,
∴ ∠2=____(______________________)
∵ ∠1=∠2
∴ ∠1=∠3(____________)
∴ AB∥_____(_____________________)
∴∠BAC+______=180°(_____________________)
∵ ∠BAC=70°
∴ ∠AGD=_______
∠AGD
DG
∠3
110°
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,同旁内角互补
练习3:
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?
A
B
D
C
E
2
4
3
1
5、例题讲解
1、如图是梯形有上底的一部分,已经量得∠A=115°, ∠D=100°,那么梯形的另外两个角各是多少度?
2、如图,AB∥DE,BC∥EF,BC交DE于点G,∠B与∠E有什么关系?为什么?
B
A
G
E
D
C
F
3、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数 。
6、课堂小结
E
F
A
B
C
D
1
2
4
3
8
5
6
7
本节课你学到了哪些知识?
(1)平行线的性质有哪三条?
(2)如何区分平行线的判定和性质?
平行线的性质有以下三条,
(1)两直线平行,同位角相等,
(2)两直线平行,内错角相等,
(3)两直线平行,同旁内角互补.
由角的已知条件推出两直线平行的结论是平行线的判定;而由两直线平行的条件推出角的结论则是平行线的性质.
P25 : 4、5、6、7
