六年级上册数学教案-同步教程:分数乘法 人教版(无答案)
文档属性
| 名称 | 六年级上册数学教案-同步教程:分数乘法 人教版(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 22:05:02 | ||
图片预览

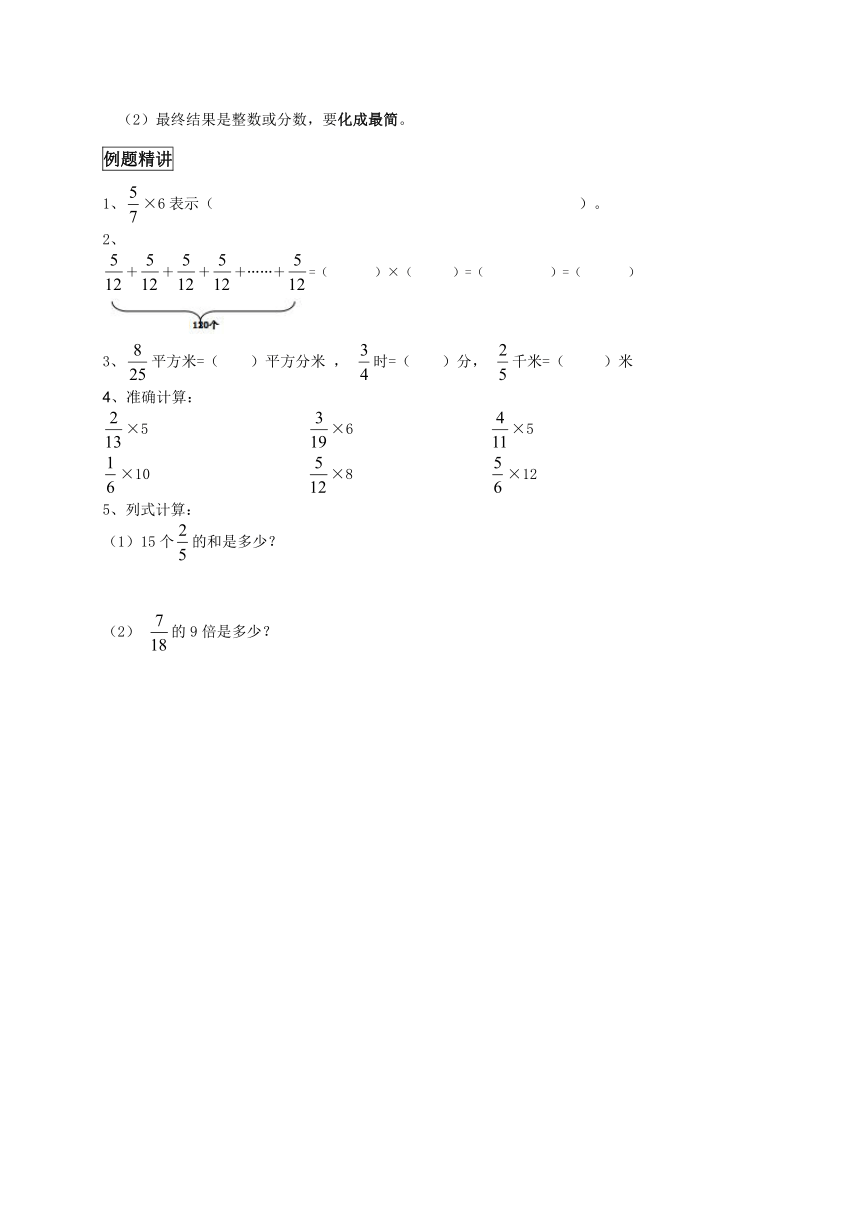

文档简介
授课教师 上课时间 年 月 日 第( )次课 课时:3课时
教学课题 分数乘法(1)
教学内容 理解分数乘整数、分数乘分数的意义;掌握分数乘整数的计算法则;掌握分数乘分数的计算法则。
教学重点/难点 分数乘法的意义的应用;分数化简约分和计算能力。
课后作业 根据学生上课情况布置
知识点一:分数乘整数的意义
1、分数乘整数的意义与整数乘法的意义相同,都是求几个相同的数相加的和的简便运算。
2、求一个分数的几倍是多少或求几个相同分数的和是多少,就用这个分数乘“几”。
知识点二:分数乘整数的计算法则
分数乘整数,用分数的分子和整数相乘的积做分子,分母不变。(能用简便运算的,整数和分母可以约分的要先约分,约分后再和分子相乘做分子。)
【注意事项】
(1)为了计算简便,能约分的要先约分,再计算。
(2)最终结果是整数或分数,要化成最简。
例题精讲
1、×6表示( )。
2、
++++……+=( )×( )=( )=( )
3、平方米=( )平方分米 , 时=( )分, 千米=( )米
4、准确计算:
×5 ×6 ×5
×10 ×8 ×12
5、列式计算:
(1)15个的和是多少?
(2) 的9倍是多少?
(3)一个正三角形边长分米,它的周长有多少厘米?
(4)一种花生每千克约含油千克,1吨花生约含油多少千克?
(5)一批大米,每天吃去吨,3天一共吃去多少吨?
(6)小华和小明骑自行车上学,小华每分钟行千米,小明每小时行15千米。他俩谁骑的速度快?
知识点三:一个数乘分数的意义
一个数乘分数的意义就是求一个数的几分之几是多少。
知识点四:分数乘分数的计算法则
分数乘分数的计算方法:分子相乘的积作分子,分母相乘的积作分母。
可用字母表示为: 。
【注意事项】
(1) 分数乘分数的计算方法也适用于小数乘分数,先把小数化成分数,然后计算。例如。
(1) 分数乘分数,这里的分数也可以是带分数,计算时先把带分数化成假分数。例如。
例题精讲
1、35是40的,35比40少。
2、×表示( )
3、米的是( )米; 公顷的是( )公顷。
4、(判断)kg的蛋糕,吃了,还剩kg。( )
5、计算下列各题:
× × ×
12× × ×
6、列出下列各题并计算
(1)的是多少?
(2)一个西瓜平均分成两半,再在切开的两块西瓜上分别平均分成两份,那么切好的每份西瓜是原来整个西瓜的几分之几?
7、计算下列各题
(1)一杯牛奶重千克,那么杯牛奶重多少千克?
(2)一个平行四边形的高是米,它的底是高的,它的面积是多少平方米?
(3)修路队修路,上午修了千米,下午修的是上午的,这一天修了多少千米?
知识点五:乘法中比较大小的规律
一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
例题精讲
1、在○里填上“>”、“<”或“=”。
×○ × ○ ×○
× ○ ×21 ○ ×1 ○
× ○ × ○ ×○
× ○ × 1 ○ ×0 ○
分数乘法意义和计算法则
教学课题 分数乘法(1)
教学内容 理解分数乘整数、分数乘分数的意义;掌握分数乘整数的计算法则;掌握分数乘分数的计算法则。
教学重点/难点 分数乘法的意义的应用;分数化简约分和计算能力。
课后作业 根据学生上课情况布置
知识点一:分数乘整数的意义
1、分数乘整数的意义与整数乘法的意义相同,都是求几个相同的数相加的和的简便运算。
2、求一个分数的几倍是多少或求几个相同分数的和是多少,就用这个分数乘“几”。
知识点二:分数乘整数的计算法则
分数乘整数,用分数的分子和整数相乘的积做分子,分母不变。(能用简便运算的,整数和分母可以约分的要先约分,约分后再和分子相乘做分子。)
【注意事项】
(1)为了计算简便,能约分的要先约分,再计算。
(2)最终结果是整数或分数,要化成最简。
例题精讲
1、×6表示( )。
2、
++++……+=( )×( )=( )=( )
3、平方米=( )平方分米 , 时=( )分, 千米=( )米
4、准确计算:
×5 ×6 ×5
×10 ×8 ×12
5、列式计算:
(1)15个的和是多少?
(2) 的9倍是多少?
(3)一个正三角形边长分米,它的周长有多少厘米?
(4)一种花生每千克约含油千克,1吨花生约含油多少千克?
(5)一批大米,每天吃去吨,3天一共吃去多少吨?
(6)小华和小明骑自行车上学,小华每分钟行千米,小明每小时行15千米。他俩谁骑的速度快?
知识点三:一个数乘分数的意义
一个数乘分数的意义就是求一个数的几分之几是多少。
知识点四:分数乘分数的计算法则
分数乘分数的计算方法:分子相乘的积作分子,分母相乘的积作分母。
可用字母表示为: 。
【注意事项】
(1) 分数乘分数的计算方法也适用于小数乘分数,先把小数化成分数,然后计算。例如。
(1) 分数乘分数,这里的分数也可以是带分数,计算时先把带分数化成假分数。例如。
例题精讲
1、35是40的,35比40少。
2、×表示( )
3、米的是( )米; 公顷的是( )公顷。
4、(判断)kg的蛋糕,吃了,还剩kg。( )
5、计算下列各题:
× × ×
12× × ×
6、列出下列各题并计算
(1)的是多少?
(2)一个西瓜平均分成两半,再在切开的两块西瓜上分别平均分成两份,那么切好的每份西瓜是原来整个西瓜的几分之几?
7、计算下列各题
(1)一杯牛奶重千克,那么杯牛奶重多少千克?
(2)一个平行四边形的高是米,它的底是高的,它的面积是多少平方米?
(3)修路队修路,上午修了千米,下午修的是上午的,这一天修了多少千米?
知识点五:乘法中比较大小的规律
一个数(0除外)乘大于1的数,积大于这个数。
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。
例题精讲
1、在○里填上“>”、“<”或“=”。
×○ × ○ ×○
× ○ ×21 ○ ×1 ○
× ○ × ○ ×○
× ○ × 1 ○ ×0 ○
分数乘法意义和计算法则
