高中数学人教A版必修第一册课件5.6.2正弦型函数 y=Asin( ωx+φ) 课件(共36张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件5.6.2正弦型函数 y=Asin( ωx+φ) 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 22:43:50 | ||
图片预览







文档简介
(共36张PPT)
正弦型函数
y = A sin(ωx+ )
新课引入
筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.
假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.你能用一个合适的函数模型来刻画盛水筒(视为质点)距离水面的相对高度与时间的关系吗?
新课引入
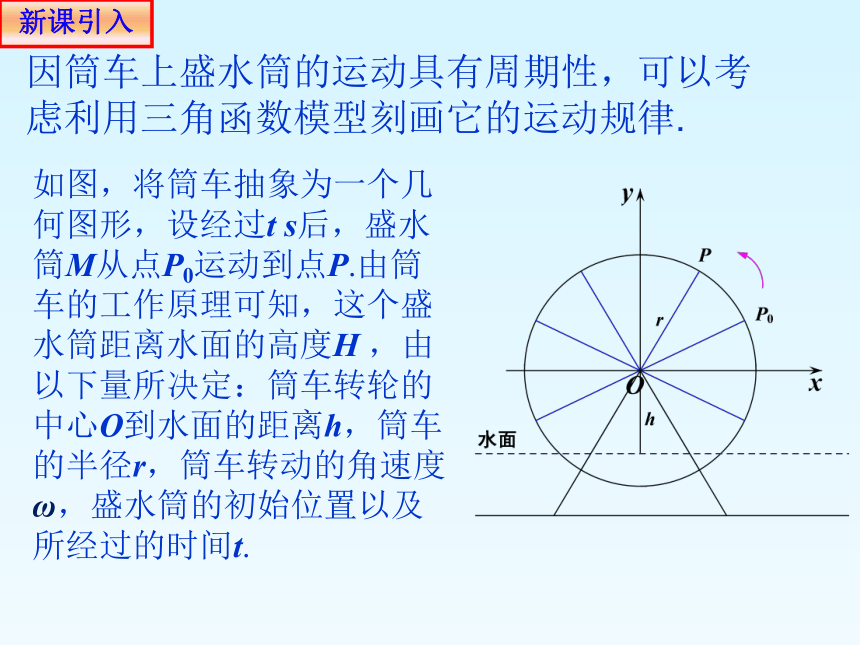
因筒车上盛水筒的运动具有周期性,可以考虑利用三角函数模型刻画它的运动规律.
如图,将筒车抽象为一个几何图形,设经过t s后,盛水筒M从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H ,由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω,盛水筒的初始位置以及所经过的时间t.
新课引入
下面我们分析这些量的相互关系,进而建立盛水筒M运动的数学模型.
如图,以O为原点,以与水平面平行的直线为x轴建立直角坐标系.设t=0时,盛水筒M位于点P0,以Ox为始边,OP0为终边的角为φ,经过t s后运动到点P(x,y).于是,以Ox为始边,OP为终边的角为ωx+φ,并且有y=rsin(ωt+φ)
所以,盛水筒M距离水面的高度H与时间t的关系是
H=rsin(ωt+φ)+h
y = A sin(ωx+ )
(其中A 、ω 、 为常数。
正弦型函数
不妨设A>0,ω>0)
A为振幅,
为 频率,
ωx+ 为相位,x=0 时的相位 为初相。
为周期
周期T的倒数
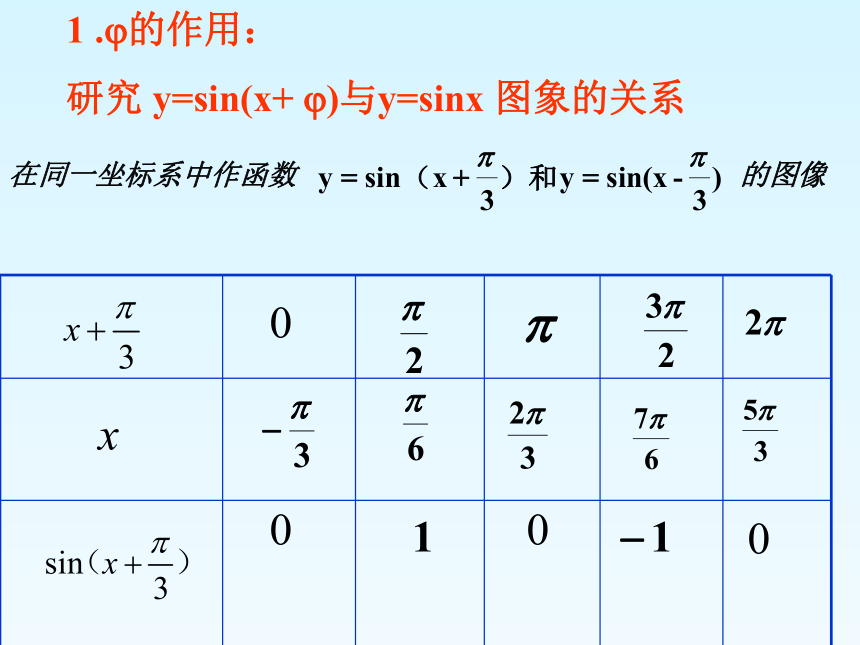
1 . 的作用:
研究 y=sin(x+ )与y=sinx 图象的关系
在同一坐标系中作函数
的图像
)
3
-
sin(x
y
3
x
sin
y
p
p
=
+
=
)和
(
0
1
0
-1
0
0
(π/3,0)
(2π/3,0)
(5π/3,0)
(7π/3,0)
(π/6,1)
(7π/6,-1)
(-π/3,0)
x
y
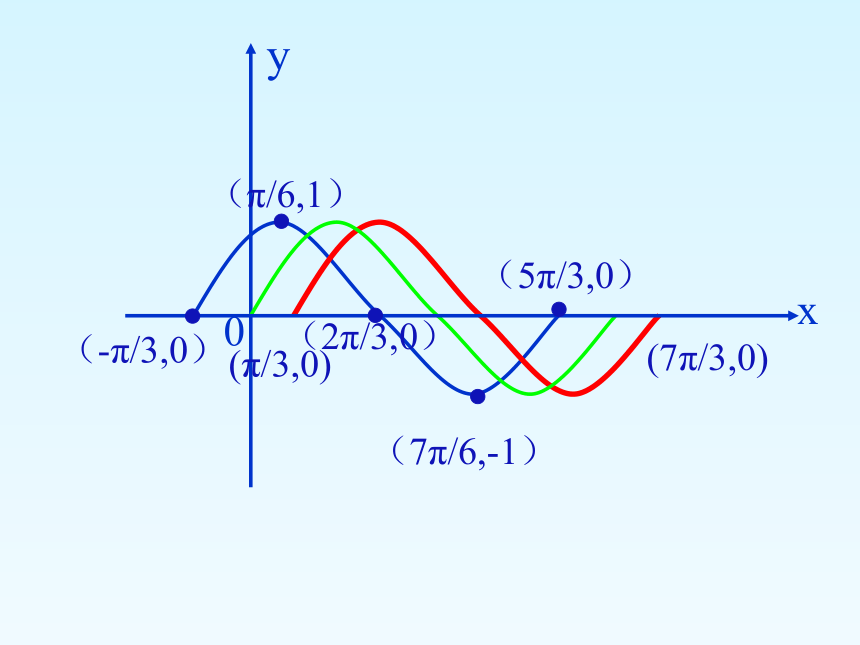
的图象,可以看作是把正弦曲线y=sinx上的所有的点向左( )或向右( )平行移动 个单位长度而得到.
你能得到y=sin(x+ )与y=sinx 图象的关系吗?
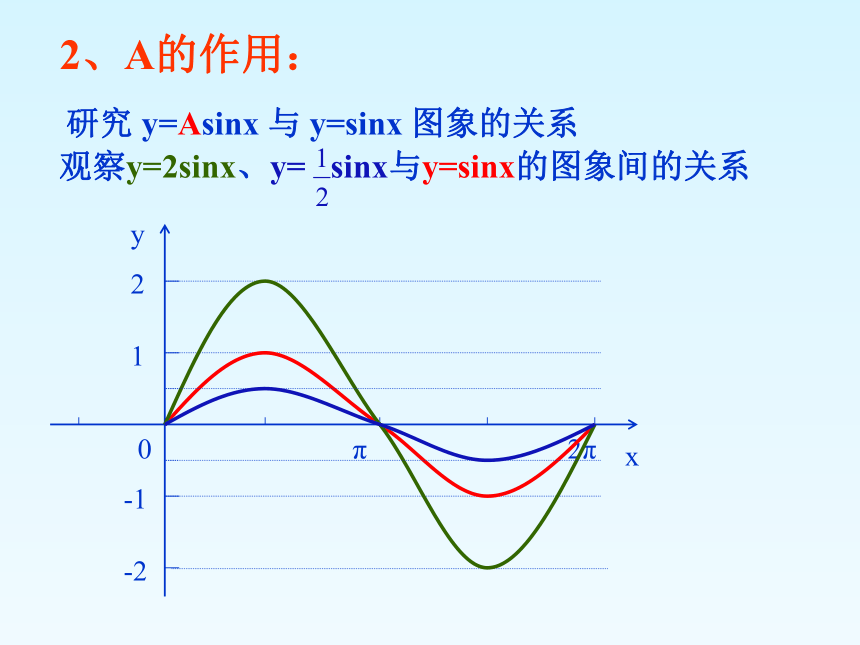
研究 y=Asinx 与 y=sinx 图象的关系
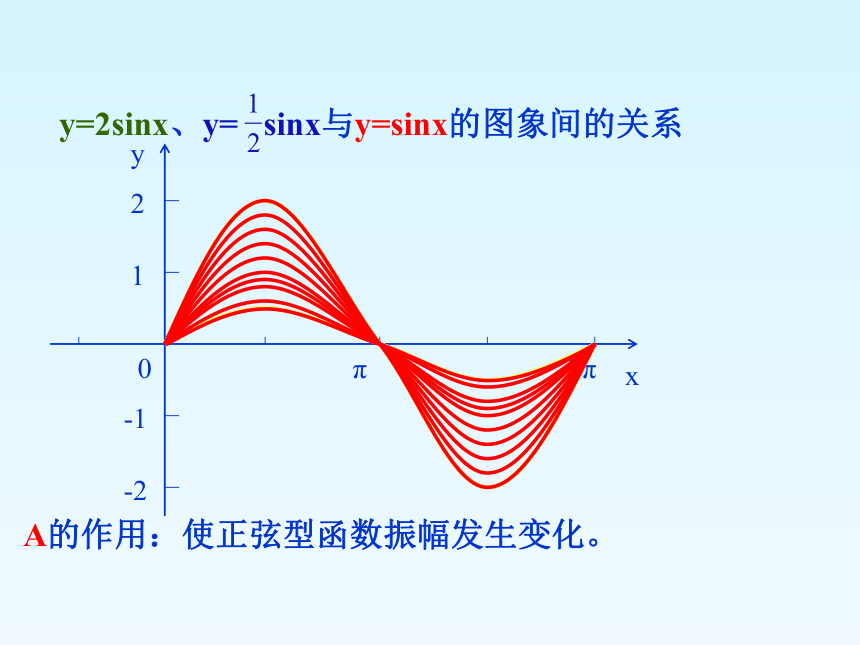
观察y=2sinx、y= sinx与y=sinx的图象间的关系
y
0
x
π
2π
1
2
-1
-2
2、A的作用:
y
0
x
π
2π
1
2
-1
-2
A的作用:使正弦型函数振幅发生变化。
y=2sinx、y= sinx与y=sinx的图象间的关系
y=Asinx(A>0, A 1)的图象是由y=sinx的图象上所有点的横坐标不变,纵坐标伸长 (当A>1时)或压缩(当0你能得到y=Asinx与y=sinx 图象的关系吗?
研究 y=sinωx与y=sinx 图象的关系
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
作y=sinx的图象
观察y=sin2x、y=sin 与y=sinx的图象间的关系
x 0 2
sinx 0 1 0 -1 0
3、ω的作用:
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
作y=sin2x的图象
观察y=sin2x、y=sin x与y=sinx的图象间的关系
2x 0 2
x 0
sin2x 0 1 0 -1 0
3、ω的作用:
x 0 2
x 0 2 3 4
sin x 0 1 0 -1 0
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
y=sin2x、y=sin x与y=sinx的图象间的关系
作y=sin x的图象
y
0
x
π
2π
3π
4π
1
-1
ω的作用:使正弦型函数的周期发生变化。
通过观察y=sin2x、y=sin x与y=sinx的图象间的关系
研究 y=sinωx与y=sinx 图象的关系
函数 的图象可以看作是把 的图象上所有点的横坐标伸长( )或缩短( )到原来的 倍(纵坐标不变)而得到的.
你能得到 与 图象的关系吗?
y
0
x
π
2π
3π
4π
1
-1
y=sin2x y=sin x y=sinx
ω
A
y
0
x
π
2π
1
-1
y = sin(x+ ) y = sin(x - )
y=sinx
y=2sinx y= sinx y=sinx
y
0
x
π
2π
1
2
-1
-2
相位变换
振幅变换
周期变换
数学应用:
例1 若函数 表示一个振动量:
⑴求这个振动的振幅、周期、初相;画出该函数的简图;
⑶根据函数的简图,写出函数的单调区间.
解:设 ,则
y
x
O
3
-3
y
x
O
3
-3
(2)描点
(3)连线
解:可令
求单调减区间,可令
解得:
解得:
原函数的单调递增区间为:
单调递减区间为:
整体法求单调增区间
y=3sin(2x+ )
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=sin(x+ )
y=sin(2x+ )
y=3sin(2x+ )
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=sin2x
y=3sin2x
y=3sin(2x+ )
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
函数 y=sinx y=sin(2x ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(2)向左平移
纵坐标不变
(1)横坐标缩短到原来的 倍
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin(x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0y=ASin( x+ )的图象
(1)向左( >0)或向右( < 0)
平移| |个单位
(2)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin x 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0y=ASin( x+ )的图象
(2)向左( >0)或向右( <0)
平移| |个单位
(1)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
例2.如图为函数
的图象的一段,求其解析式.
练习. 函数f(x)=Asin(ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,求f(x).
一、作函数y=Asin( x+ ) 的图象:
(1)用“五点法”作图。1、列五点表2、描点 3 、连线
(2)利用变换关系作图。
二、函数 y = sinx 的图象与函数 y=Asin( x+ )
的图象间的变换关系。
三、由图像求解析式。
小 结
用五点法作出y=Asin(ωx+ )在一个周期内的图象,
先由 A 确定振幅,求出最值;
再由 ωx+ =0 确定 xo ;
列五点表,
准备工作
最后由ω确定周期 T,求出
1
2
A
A
A
A
3
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
描点、连线。
C
巩固练习
B
巩固练习
C
巩固练习
D
巩固练习
C
正弦型函数
y = A sin(ωx+ )
新课引入
筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.
假定在水流量稳定的情况下,筒车上的每一个盛水筒都做匀速圆周运动.你能用一个合适的函数模型来刻画盛水筒(视为质点)距离水面的相对高度与时间的关系吗?
新课引入
因筒车上盛水筒的运动具有周期性,可以考虑利用三角函数模型刻画它的运动规律.
如图,将筒车抽象为一个几何图形,设经过t s后,盛水筒M从点P0运动到点P.由筒车的工作原理可知,这个盛水筒距离水面的高度H ,由以下量所决定:筒车转轮的中心O到水面的距离h,筒车的半径r,筒车转动的角速度ω,盛水筒的初始位置以及所经过的时间t.
新课引入
下面我们分析这些量的相互关系,进而建立盛水筒M运动的数学模型.
如图,以O为原点,以与水平面平行的直线为x轴建立直角坐标系.设t=0时,盛水筒M位于点P0,以Ox为始边,OP0为终边的角为φ,经过t s后运动到点P(x,y).于是,以Ox为始边,OP为终边的角为ωx+φ,并且有y=rsin(ωt+φ)
所以,盛水筒M距离水面的高度H与时间t的关系是
H=rsin(ωt+φ)+h
y = A sin(ωx+ )
(其中A 、ω 、 为常数。
正弦型函数
不妨设A>0,ω>0)
A为振幅,
为 频率,
ωx+ 为相位,x=0 时的相位 为初相。
为周期
周期T的倒数
1 . 的作用:
研究 y=sin(x+ )与y=sinx 图象的关系
在同一坐标系中作函数
的图像
)
3
-
sin(x
y
3
x
sin
y
p
p
=
+
=
)和
(
0
1
0
-1
0
0
(π/3,0)
(2π/3,0)
(5π/3,0)
(7π/3,0)
(π/6,1)
(7π/6,-1)
(-π/3,0)
x
y
的图象,可以看作是把正弦曲线y=sinx上的所有的点向左( )或向右( )平行移动 个单位长度而得到.
你能得到y=sin(x+ )与y=sinx 图象的关系吗?
研究 y=Asinx 与 y=sinx 图象的关系
观察y=2sinx、y= sinx与y=sinx的图象间的关系
y
0
x
π
2π
1
2
-1
-2
2、A的作用:
y
0
x
π
2π
1
2
-1
-2
A的作用:使正弦型函数振幅发生变化。
y=2sinx、y= sinx与y=sinx的图象间的关系
y=Asinx(A>0, A 1)的图象是由y=sinx的图象上所有点的横坐标不变,纵坐标伸长 (当A>1时)或压缩(当0
研究 y=sinωx与y=sinx 图象的关系
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
作y=sinx的图象
观察y=sin2x、y=sin 与y=sinx的图象间的关系
x 0 2
sinx 0 1 0 -1 0
3、ω的作用:
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
作y=sin2x的图象
观察y=sin2x、y=sin x与y=sinx的图象间的关系
2x 0 2
x 0
sin2x 0 1 0 -1 0
3、ω的作用:
x 0 2
x 0 2 3 4
sin x 0 1 0 -1 0
y
0
x
π
2π
3π
4π
1
-1
1、列表
2、描点
3、连线
y=sin2x、y=sin x与y=sinx的图象间的关系
作y=sin x的图象
y
0
x
π
2π
3π
4π
1
-1
ω的作用:使正弦型函数的周期发生变化。
通过观察y=sin2x、y=sin x与y=sinx的图象间的关系
研究 y=sinωx与y=sinx 图象的关系
函数 的图象可以看作是把 的图象上所有点的横坐标伸长( )或缩短( )到原来的 倍(纵坐标不变)而得到的.
你能得到 与 图象的关系吗?
y
0
x
π
2π
3π
4π
1
-1
y=sin2x y=sin x y=sinx
ω
A
y
0
x
π
2π
1
-1
y = sin(x+ ) y = sin(x - )
y=sinx
y=2sinx y= sinx y=sinx
y
0
x
π
2π
1
2
-1
-2
相位变换
振幅变换
周期变换
数学应用:
例1 若函数 表示一个振动量:
⑴求这个振动的振幅、周期、初相;画出该函数的简图;
⑶根据函数的简图,写出函数的单调区间.
解:设 ,则
y
x
O
3
-3
y
x
O
3
-3
(2)描点
(3)连线
解:可令
求单调减区间,可令
解得:
解得:
原函数的单调递增区间为:
单调递减区间为:
整体法求单调增区间
y=3sin(2x+ )
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=sin(x+ )
y=sin(2x+ )
y=3sin(2x+ )
1
-1
2
-2
o
x
y
3
-3
2
y=sinx
y=sin2x
y=3sin2x
y=3sin(2x+ )
函数 y=sinx y=sin(x+ ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(1)向左平移
纵坐标不变
(2)横坐标缩短到原来的 倍
函数 y=sinx y=sin(2x ) 的图象
(3)横坐标不变
纵坐标伸长到原来的3倍
y=3sin(2x+ )的图象
y=sin(2x+ ) 的图象
(2)向左平移
纵坐标不变
(1)横坐标缩短到原来的 倍
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin(x+ ) 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0
(1)向左( >0)或向右( < 0)
平移| |个单位
(2)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
y=Sin( x+ ) 的图象
函数 y=Sinx y=Sin x 的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0
(2)向左( >0)或向右( <0)
平移| |个单位
(1)横坐标缩短( >1)或伸长(0< <1)到
原来的 倍,纵坐标不变
例2.如图为函数
的图象的一段,求其解析式.
练习. 函数f(x)=Asin(ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,求f(x).
一、作函数y=Asin( x+ ) 的图象:
(1)用“五点法”作图。1、列五点表2、描点 3 、连线
(2)利用变换关系作图。
二、函数 y = sinx 的图象与函数 y=Asin( x+ )
的图象间的变换关系。
三、由图像求解析式。
小 结
用五点法作出y=Asin(ωx+ )在一个周期内的图象,
先由 A 确定振幅,求出最值;
再由 ωx+ =0 确定 xo ;
列五点表,
准备工作
最后由ω确定周期 T,求出
1
2
A
A
A
A
3
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
ωx+ =0 xo
描点、连线。
C
巩固练习
B
巩固练习
C
巩固练习
D
巩固练习
C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
