高中数学人教A版必修第一册课件5.4.2 正、余弦函数的性质 课件(共15张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件5.4.2 正、余弦函数的性质 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 442.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 22:53:36 | ||
图片预览




文档简介
(共15张PPT)
5.4.2 正弦函数、余弦函数的性质2
第五章 三角函数
定义域
值域
最大值
最小值
奇偶性
周期性
y=sinx
y=cosx
函数
性质
R
R
[-1,1]
[-1,1]
仅当
时取得最大值1
仅当
时取得最大值1
仅当
时取得最小值-1
仅当
时取得最小值-1
奇函数
偶函数
2π
2π
旧知回顾
对称轴:
对称中心:
3.2对称性
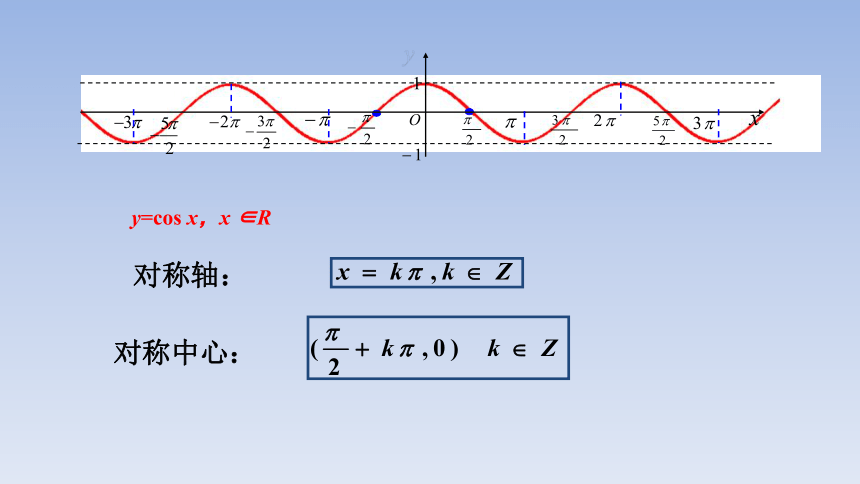
y=sin x,x ∈R
对称轴:
对称中心:
y=cos x,x ∈R
练习
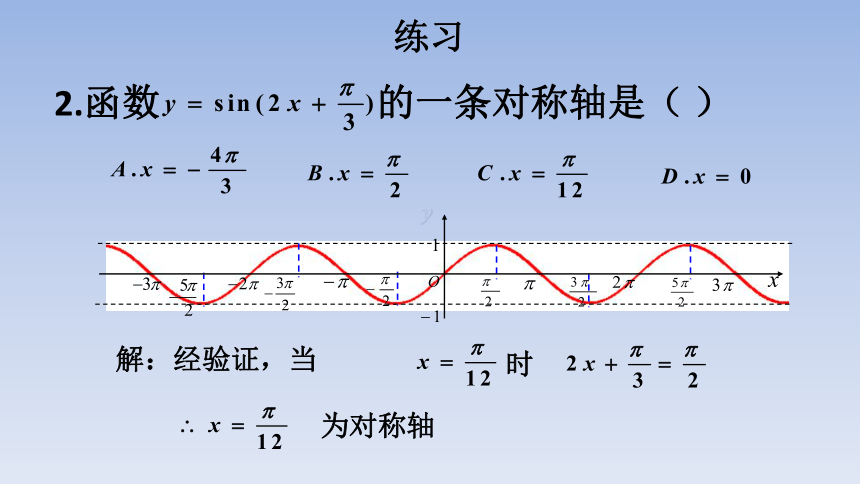
2.函数 的一条对称轴是( )
解:经验证,当
时
为对称轴
求函数 的对称轴和对称中心
解(1)令
则
的对称轴为
解得:对称轴为
的对称中心为
对称中心为
【探究】由于正弦函数是周期函数,我们可以先在它的一个周期的区间里如
讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
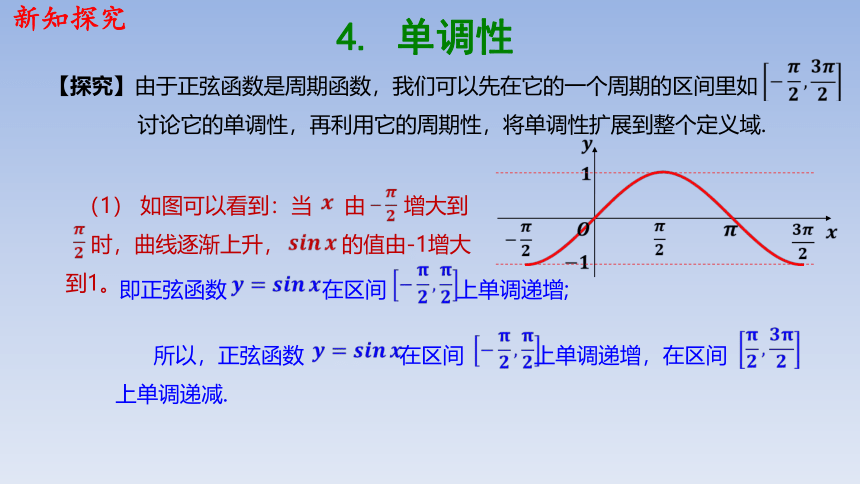
(1) 如图可以看到:当 由 增大到
时,曲线逐渐上升, 的值由-1增大
到1。
即正弦函数 在区间 上单调递增;
4. 单调性
所以,正弦函数 在区间 上单调递增,在区间
上单调递减.
新知探究
正弦函数的单调区间:
正弦函数在每一个闭区间 上都单调递增,其值从-1增
大到1;在每一个闭区间 上都单调递减,其值从1减小到-1.
由上述结果结合正弦函数的周期性我们可以知道:
余弦函数的单调区间?
函 数 名 递增区间 递减区间
y=sinx
y=cosx
正弦、余弦函数的单调性
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
例1 不通过求值,比较下列各数的大小:
教学应用
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
(1) ;
(2) .
例1 不通过求值,比较下列各数的大小:
解:令 ,则 .
因为 的单调递增区间是 ,
且由 得 ,
所以,函数 的
单调递增区间是 .
新知探究
例2 求函数 的单调递增区间.
1. 求使下列函数取得最大值、最小值的自变量的集合,并求出最大值、最小值.
(2) y=cos x+1,x∈R;
(1) y=-3sin 2x,x∈R;
解: (1)令z=2x,使函数y=-3sin z取得最大值z的集合,就是使y=sin z取得最小值的z的集合
由 ,得 .所以,使函数y=-3sin 2x取得最大值的x的集合是
同理,使函数y=-3sin 2x取得最小值x的集合是
函数y=-3sin 2x的最大值是3,最小值是-3.
练习
正弦、余弦函数的单调性
单调性
单调区间
[ +2k , +2k ],k Z
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
课堂小结
单调递增
5.4.2 正弦函数、余弦函数的性质2
第五章 三角函数
定义域
值域
最大值
最小值
奇偶性
周期性
y=sinx
y=cosx
函数
性质
R
R
[-1,1]
[-1,1]
仅当
时取得最大值1
仅当
时取得最大值1
仅当
时取得最小值-1
仅当
时取得最小值-1
奇函数
偶函数
2π
2π
旧知回顾
对称轴:
对称中心:
3.2对称性
y=sin x,x ∈R
对称轴:
对称中心:
y=cos x,x ∈R
练习
2.函数 的一条对称轴是( )
解:经验证,当
时
为对称轴
求函数 的对称轴和对称中心
解(1)令
则
的对称轴为
解得:对称轴为
的对称中心为
对称中心为
【探究】由于正弦函数是周期函数,我们可以先在它的一个周期的区间里如
讨论它的单调性,再利用它的周期性,将单调性扩展到整个定义域.
(1) 如图可以看到:当 由 增大到
时,曲线逐渐上升, 的值由-1增大
到1。
即正弦函数 在区间 上单调递增;
4. 单调性
所以,正弦函数 在区间 上单调递增,在区间
上单调递减.
新知探究
正弦函数的单调区间:
正弦函数在每一个闭区间 上都单调递增,其值从-1增
大到1;在每一个闭区间 上都单调递减,其值从1减小到-1.
由上述结果结合正弦函数的周期性我们可以知道:
余弦函数的单调区间?
函 数 名 递增区间 递减区间
y=sinx
y=cosx
正弦、余弦函数的单调性
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
例1 不通过求值,比较下列各数的大小:
教学应用
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
(1) ;
(2) .
例1 不通过求值,比较下列各数的大小:
解:令 ,则 .
因为 的单调递增区间是 ,
且由 得 ,
所以,函数 的
单调递增区间是 .
新知探究
例2 求函数 的单调递增区间.
1. 求使下列函数取得最大值、最小值的自变量的集合,并求出最大值、最小值.
(2) y=cos x+1,x∈R;
(1) y=-3sin 2x,x∈R;
解: (1)令z=2x,使函数y=-3sin z取得最大值z的集合,就是使y=sin z取得最小值的z的集合
由 ,得 .所以,使函数y=-3sin 2x取得最大值的x的集合是
同理,使函数y=-3sin 2x取得最小值x的集合是
函数y=-3sin 2x的最大值是3,最小值是-3.
练习
正弦、余弦函数的单调性
单调性
单调区间
[ +2k , +2k ],k Z
[ +2k , +2k ],k Z
单调递减
[ +2k , 2k ],k Z
单调递增
[2k , 2k + ], k Z
单调递减
函数
余弦函数
正弦函数
求函数的单调区间:
1. 直接利用相关性质
2. 复合函数的单调性
3. 利用图象寻找单调区间
课堂小结
单调递增
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
