高中数学人教A版必修第一册课件5.7三角函数的应用 课件(共18张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册课件5.7三角函数的应用 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-06 22:55:17 | ||
图片预览





文档简介
(共18张PPT)
5.7 三角函数的应用
数学(人教版)
必修第一册
第五章 三角函数
教学目标
新课程标准 核心素养
1.会用三角函数解决简单的实际问题. 数学建模、
数学运算
2.体会可以利用三角函数构建刻画事物周期变化的数学模型. 数学建模、
数学运算
重点: 分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立三角函数模型,用三角函数模型解决一些具有周期变化规律的实际问题.
难点: 将某些实际问题抽象为三角函数的模型,并调动相关学科的知识来解决问题.
整体感知
弹簧振子模型
把一个有孔的小球装在弹簧的一端,弹簧的另一端固定,在理想状态下,将小球拉离平衡位置,然后放开,他就会在平衡位置附近振动。这样的系统称为弹簧振子。
如何将弹簧振子模型转化为数学模型?
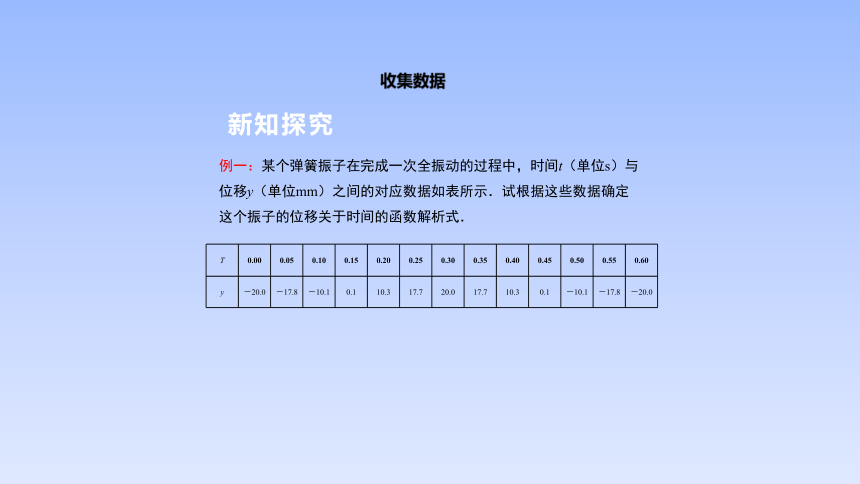
T 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60
y -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0 17.7 10.3 0.1 -10.1 -17.8 -20.0
新知探究
例一:某个弹簧振子在完成一次全振动的过程中,时间t(单位s)与位移y(单位mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
收集数据
根据散点图(如图),
分析得出位移y随时间t的变化规律可以用y=Asin(ωx+φ)这个函数模型进行刻画.
新知探究
问题 画出散点图并观察,位移y随时间t的变化规律可以用怎样的函数模型进行刻画?
画散点图
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此A=20;
振子振动的周期为0.6s,即 ,解得 ;
再由初始状态(t=0)振子的位移为-20,可得sin φ=-1,因此 。
函数的解析式为
新知探究
由数据表和散点图,你能说出振子振动时位移
y=Asin(ωx+φ)的最大值A,周期T,初始状态(t=0)时的位移吗?根据这些值,你能求出函数的解析式吗?
函数模型
注意定义域!!!
8
模型建立一般程序
研探新知
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,
模型二:交变电流
播放动画:交变电流的产生
因为交变电流随着时间呈周期性变化,所以可以用交变电流与时间的三角函数关系来刻画交变电流的周期性变化.
新知探究
问题 如何利用三角函数刻画交变电流的周期性变化?
交变电流模型
(1)求电流i随时间t变化的函数解析式;
(2)当 时,求电流i.
图(1)
图(2)
新知探究
例2 如图(1)所示的是某次实验测得的交变电流i(单位A)随时间t(单位s)变化的图象.将测得的图象放大,得到图(2).
典例分析
由交变电流的产生原理可知,电流i随时间t的变化规律可以用
来刻画.
新知探究
问题 观察图象,交变电流i随时间t的变化满足怎样的函数模型?
典例分析
解: ,初始状态的电流为4.33 A.
由这些值可求得电流i随时间t的变化的解析式是
新知探究
问题 根据图象,你能说出电流的的最大值A,周期T,初始状态(t=0)时的电流吗?由这些值,你能进一步解决问题(1)、(2)吗?
典例分析
练习3:一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压U(单位V)关于时间t(单位s)的函数解析式.
答案:周期为0.02,频率为50,电压的最大值为311 V.
电压和时间的函数解析式为U=311sin100πt,t∈[0,+ ∞) .
新知探究
巩固练习
问题
1、对于一个周期性现象,你该如何利用三角函数来刻画?
2、你能举出一些符合三角函数规律的实际模型吗?
3、在本节课中,你经历了怎样的学习过程,
4、涉及哪些数学思想方法,
5、还有哪些其它方面的收获?
课堂小结,领悟提升
归纳小结
利用三角函数刻画周期性现象,就是要找出这一现象中哪两个变量满足“当其中一个变量增加相同的常数时,另一个变量的值重复出现”,并求出这两个变量之间满足的三角函数关系.
物理中的简谐运动和交变电流都是理想当中的三角函数模型.在本节课的学习中,我们经历了由一般到特殊,由抽象到具体学习过程,涉及到数形结合思想和数学建模思想.
课堂小结,领悟提升
作业布置,因材施教
作业:教科书习题5.7第1,2题.
(1)这个简谐运动的振幅、周期与频率各是多少?
(2)写出这个简谐运动的函数解析式.
(2)
某简谐运动的图象如图所示,试根据图象回答下列问题:
1
答案:(1)振幅是3,周期是4,频率是 ;
课堂检测
5.7 三角函数的应用
数学(人教版)
必修第一册
第五章 三角函数
教学目标
新课程标准 核心素养
1.会用三角函数解决简单的实际问题. 数学建模、
数学运算
2.体会可以利用三角函数构建刻画事物周期变化的数学模型. 数学建模、
数学运算
重点: 分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立三角函数模型,用三角函数模型解决一些具有周期变化规律的实际问题.
难点: 将某些实际问题抽象为三角函数的模型,并调动相关学科的知识来解决问题.
整体感知
弹簧振子模型
把一个有孔的小球装在弹簧的一端,弹簧的另一端固定,在理想状态下,将小球拉离平衡位置,然后放开,他就会在平衡位置附近振动。这样的系统称为弹簧振子。
如何将弹簧振子模型转化为数学模型?
T 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60
y -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0 17.7 10.3 0.1 -10.1 -17.8 -20.0
新知探究
例一:某个弹簧振子在完成一次全振动的过程中,时间t(单位s)与位移y(单位mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
收集数据
根据散点图(如图),
分析得出位移y随时间t的变化规律可以用y=Asin(ωx+φ)这个函数模型进行刻画.
新知探究
问题 画出散点图并观察,位移y随时间t的变化规律可以用怎样的函数模型进行刻画?
画散点图
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此A=20;
振子振动的周期为0.6s,即 ,解得 ;
再由初始状态(t=0)振子的位移为-20,可得sin φ=-1,因此 。
函数的解析式为
新知探究
由数据表和散点图,你能说出振子振动时位移
y=Asin(ωx+φ)的最大值A,周期T,初始状态(t=0)时的位移吗?根据这些值,你能求出函数的解析式吗?
函数模型
注意定义域!!!
8
模型建立一般程序
研探新知
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐运动可以用函数y=Asin(ωx+φ),x∈[0,+∞)表示,
模型二:交变电流
播放动画:交变电流的产生
因为交变电流随着时间呈周期性变化,所以可以用交变电流与时间的三角函数关系来刻画交变电流的周期性变化.
新知探究
问题 如何利用三角函数刻画交变电流的周期性变化?
交变电流模型
(1)求电流i随时间t变化的函数解析式;
(2)当 时,求电流i.
图(1)
图(2)
新知探究
例2 如图(1)所示的是某次实验测得的交变电流i(单位A)随时间t(单位s)变化的图象.将测得的图象放大,得到图(2).
典例分析
由交变电流的产生原理可知,电流i随时间t的变化规律可以用
来刻画.
新知探究
问题 观察图象,交变电流i随时间t的变化满足怎样的函数模型?
典例分析
解: ,初始状态的电流为4.33 A.
由这些值可求得电流i随时间t的变化的解析式是
新知探究
问题 根据图象,你能说出电流的的最大值A,周期T,初始状态(t=0)时的电流吗?由这些值,你能进一步解决问题(1)、(2)吗?
典例分析
练习3:一台发电机产生的电流是正弦式电流,电压和时间之间的关系如图所示.由图象说出它的周期、频率和电压的最大值,并求出电压U(单位V)关于时间t(单位s)的函数解析式.
答案:周期为0.02,频率为50,电压的最大值为311 V.
电压和时间的函数解析式为U=311sin100πt,t∈[0,+ ∞) .
新知探究
巩固练习
问题
1、对于一个周期性现象,你该如何利用三角函数来刻画?
2、你能举出一些符合三角函数规律的实际模型吗?
3、在本节课中,你经历了怎样的学习过程,
4、涉及哪些数学思想方法,
5、还有哪些其它方面的收获?
课堂小结,领悟提升
归纳小结
利用三角函数刻画周期性现象,就是要找出这一现象中哪两个变量满足“当其中一个变量增加相同的常数时,另一个变量的值重复出现”,并求出这两个变量之间满足的三角函数关系.
物理中的简谐运动和交变电流都是理想当中的三角函数模型.在本节课的学习中,我们经历了由一般到特殊,由抽象到具体学习过程,涉及到数形结合思想和数学建模思想.
课堂小结,领悟提升
作业布置,因材施教
作业:教科书习题5.7第1,2题.
(1)这个简谐运动的振幅、周期与频率各是多少?
(2)写出这个简谐运动的函数解析式.
(2)
某简谐运动的图象如图所示,试根据图象回答下列问题:
1
答案:(1)振幅是3,周期是4,频率是 ;
课堂检测
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
