高中数学人教A版必修第一册 第五章 三角函数5.2.1三角函数的概念2 (课件共19张PPT)
文档属性
| 名称 | 高中数学人教A版必修第一册 第五章 三角函数5.2.1三角函数的概念2 (课件共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 957.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 01:34:53 | ||
图片预览






文档简介
(共19张PPT)
5.2.2三角函数的概念(二)
复习回顾:
1. 三角函数的定义:
设α是一个任意角,点P(x, y)是α的终边与单位圆的交点,则
复习回顾:2. 三角函数的定义:
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),P与原点的距离为
,
则
复习回顾
正弦函数
余弦函数
正切函数
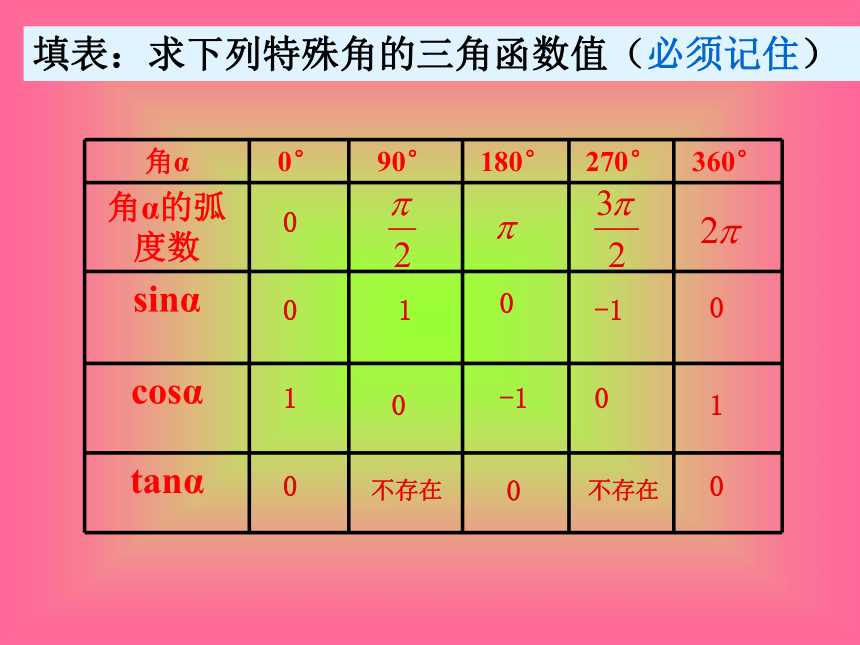
填表:求下列特殊角的三角函数值(必须记住)
角α 0° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
0
0
0
0
0
0
0
0
1
1
-1
-1
1
0
不存在
不存在
例2.设α的终边过点P(-b,4),且cosα=
则b的值是( )
解:r=
cosα=
解得b=3.
(A)3 (B)-3 (C)±3 (D)5
A
公式一
由三角函数的定义可知:
当β=2kπ+α(k∈Z)时,β与α的同名三角函数值相等。
即终边相同的角的三角函数值都相等。
其中,α是“任意角”,
例1计算下列三角函数值
交流与讨论:三角函数在各象限内的符号
角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定.
sinα
cosα
tanα
+
+
-
-
+
-
+
-
x
y
0
x
y
0
+
-
+
-
0
y
0
x
0
1
-1
1
0
-1
0
0
0
不存在
不存在
例2. 确定下列三角函数值的符号:
(1)cos250 ; (2)
(3)tan(-672 );(4)
解: (1)250 在第三象限,所以cos250 <0.
(2) - 在第四象限,所以sin(- )<0.
(3) -672 在第一象限,所以tan(-672 )>0.
(4) 在第四象限,所以tan( )<0.
例3.设sinθ<0且tanθ>0,确定θ是第几象限的角。
解:因为sinθ<0,所以θ可能是第三、四象限的角,或者其终边与y轴负半轴重合,
又tanθ>0,θ可能是第一、三象限的角,
综上所述,θ是第三象限的角。
例4.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能
B
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
3. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
4.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
解:∵P(-2, y)是角θ终边上一点, r=
5.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
作业布置:
1、课本182页: 1.3.4
2、课本182页; 5
5.2.2三角函数的概念(二)
复习回顾:
1. 三角函数的定义:
设α是一个任意角,点P(x, y)是α的终边与单位圆的交点,则
复习回顾:2. 三角函数的定义:
设α是一个任意角,在α的终边上任取(异于原点的)一点P(x, y),P与原点的距离为
,
则
复习回顾
正弦函数
余弦函数
正切函数
填表:求下列特殊角的三角函数值(必须记住)
角α 0° 90° 180° 270° 360°
角α的弧度数
sinα
cosα
tanα
0
0
0
0
0
0
0
0
1
1
-1
-1
1
0
不存在
不存在
例2.设α的终边过点P(-b,4),且cosα=
则b的值是( )
解:r=
cosα=
解得b=3.
(A)3 (B)-3 (C)±3 (D)5
A
公式一
由三角函数的定义可知:
当β=2kπ+α(k∈Z)时,β与α的同名三角函数值相等。
即终边相同的角的三角函数值都相等。
其中,α是“任意角”,
例1计算下列三角函数值
交流与讨论:三角函数在各象限内的符号
角α是“任意角”, 由三角函数定义可知,由于P(x, y)点的坐标x, y的正负是随角α所在的象限的变化而不同,所以三角函数的符号应由角α所在的象限确定.
sinα
cosα
tanα
+
+
-
-
+
-
+
-
x
y
0
x
y
0
+
-
+
-
0
y
0
x
0
1
-1
1
0
-1
0
0
0
不存在
不存在
例2. 确定下列三角函数值的符号:
(1)cos250 ; (2)
(3)tan(-672 );(4)
解: (1)250 在第三象限,所以cos250 <0.
(2) - 在第四象限,所以sin(- )<0.
(3) -672 在第一象限,所以tan(-672 )>0.
(4) 在第四象限,所以tan( )<0.
例3.设sinθ<0且tanθ>0,确定θ是第几象限的角。
解:因为sinθ<0,所以θ可能是第三、四象限的角,或者其终边与y轴负半轴重合,
又tanθ>0,θ可能是第一、三象限的角,
综上所述,θ是第三象限的角。
例4.若三角形的两内角 , 满足sin cos <0,则此三角形必为( )
A. 锐角三角形 B. 钝角三角形
C. 直角三角形 D. 以上三种情况都可能
B
练习
1.函数y= + + 的值域是 ( )
(A) {-1,1} (B) {-1,1,3}
(C) {-1,3} (D) {1,3}
C
2. 设A是第三象限角,且|sin |= -sin ,则是 ( )
(A)第一象限角 (B) 第二象限角
(C)第三象限角 (D) 第四象限角
D
3. sin2·cos3·tan4的值 ( )
(A)大于0 (B)小于0
(C)等于0 (D)不确定
B
4.若sinθ·cosθ>0, 则θ是第 象限的角
一、三
解:∵P(-2, y)是角θ终边上一点, r=
5.已知P(-2,y)是角θ终边上一点,且sinθ= - ,求cosθ的值.
解得y=-1.
所以cosθ= - .
作业布置:
1、课本182页: 1.3.4
2、课本182页; 5
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
