人教版七年级数学下册 8.3二元一次方程组的应用--几何问题 (含答案)
文档属性
| 名称 | 人教版七年级数学下册 8.3二元一次方程组的应用--几何问题 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 13:43:53 | ||
图片预览


文档简介
8.3二元一次方程组的应用--几何问题
一、选择题.
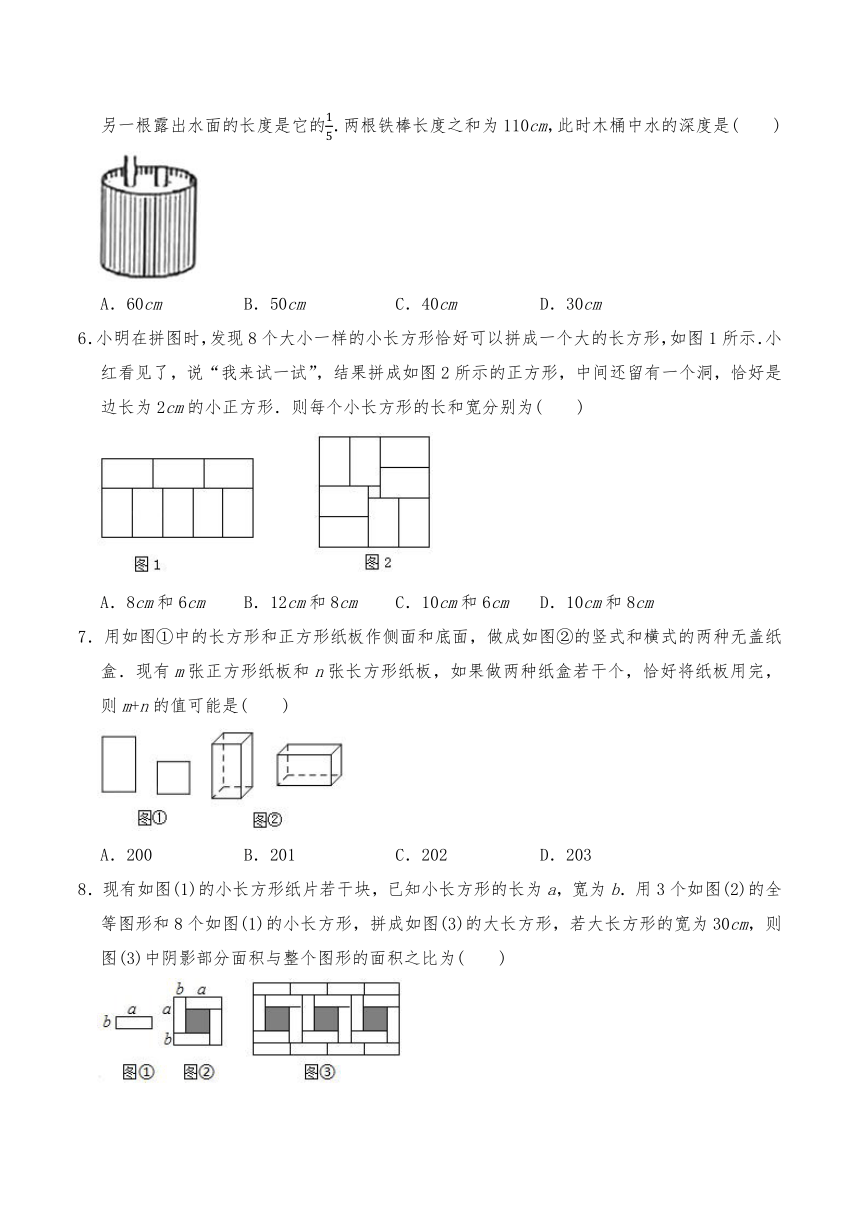
1.如图,在大长方形ABCD中,放入六个相同的小长方形,则阴影部分的面积为( )
A.140 cm2 B.96cm2 C.44 cm2 D.16 cm2
2.八块相同的长方形地砖拼成一个长方形,每块长方形地砖的宽等于( )
A.15cm B.30cm C.12cm D.10cm
3.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96 B.112 C.126 D.140
4.小林去超市帮妈妈买回一批规格一样的纸杯.如图,他把3个纸杯叠在一起高度是9cm,把8个纸杯叠在一起高度是14cm,若把50个纸杯叠在一起时,它的高度约是( )cm.
A.150cm B.56cm C.57cm D.81cm
5.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为110cm,此时木桶中水的深度是( )
A.60cm B.50cm C.40cm D.30cm
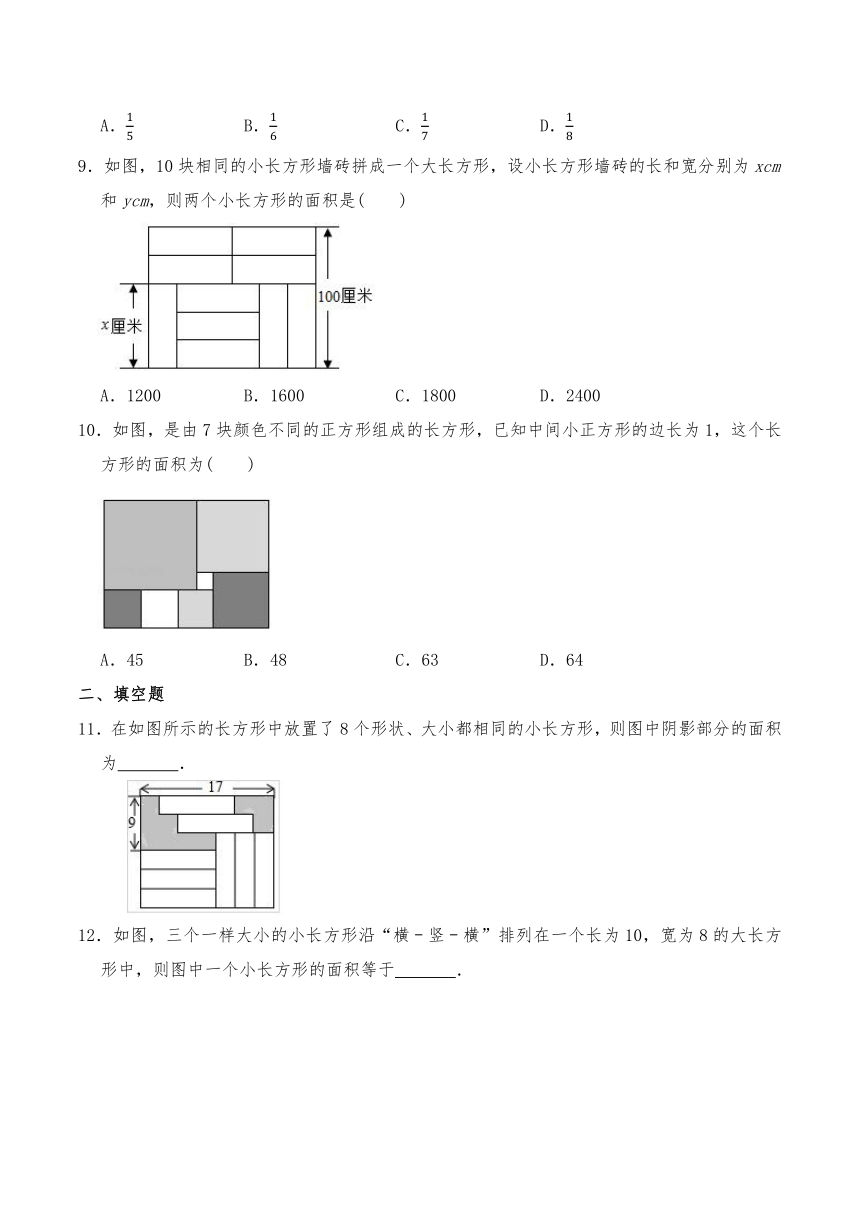
6.小明在拼图时,发现8个大小一样的小长方形恰好可以拼成一个大的长方形,如图1所示.小红看见了,说“我来试一试”,结果拼成如图2所示的正方形,中间还留有一个洞,恰好是边长为2cm的小正方形.则每个小长方形的长和宽分别为( )
A.8cm和6cm B.12cm和8cm C.10cm和6cm D.10cm和8cm
7.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
8.现有如图(1)的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图(2)的全等图形和8个如图(1)的小长方形,拼成如图(3)的大长方形,若大长方形的宽为30cm,则图(3)中阴影部分面积与整个图形的面积之比为( )
A. B. C. D.
9.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200 B.1600 C.1800 D.2400
10.如图,是由7块颜色不同的正方形组成的长方形,已知中间小正方形的边长为1,这个长方形的面积为( )
A.45 B.48 C.63 D.64
二、填空题
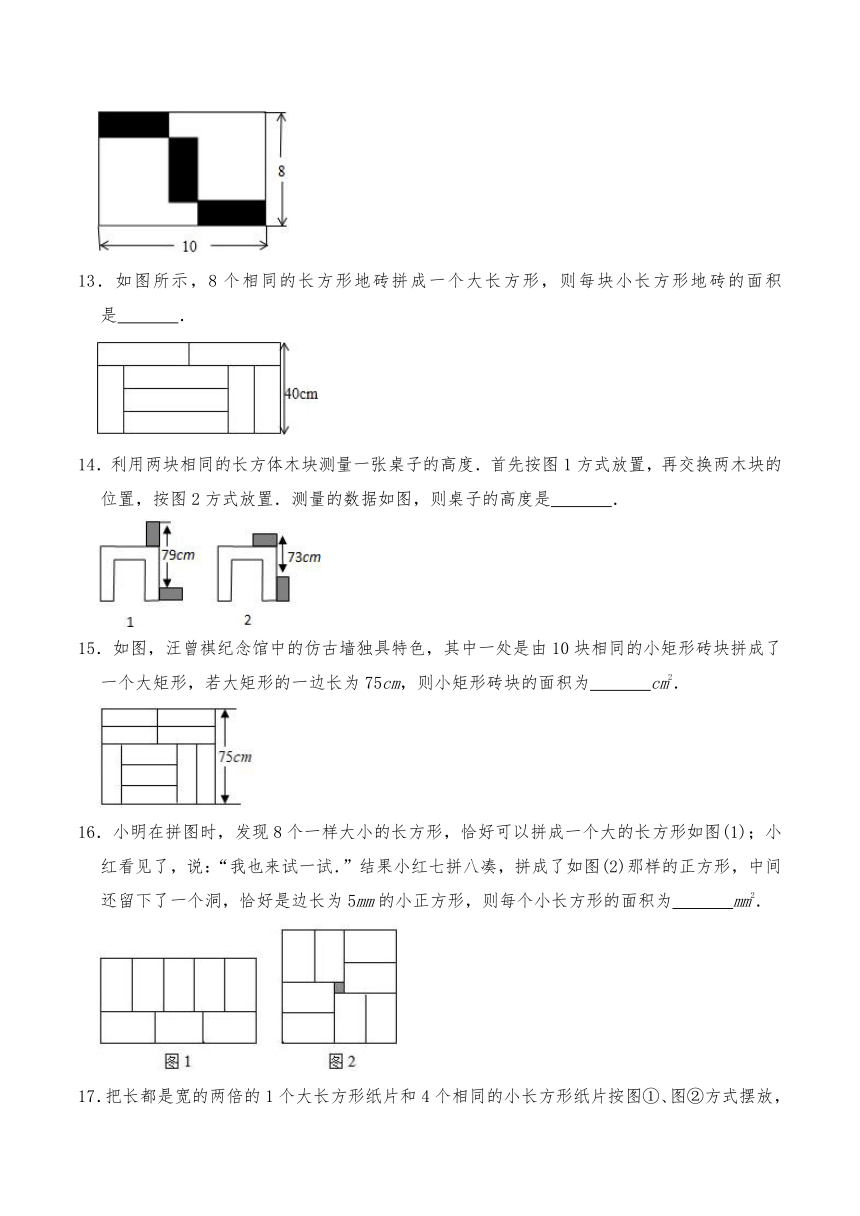
11.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
12.如图,三个一样大小的小长方形沿“横﹣竖﹣横”排列在一个长为10,宽为8的大长方形中,则图中一个小长方形的面积等于 .
13.如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是 .
14.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是 .
15.如图,汪曾祺纪念馆中的仿古墙独具特色,其中一处是由10块相同的小矩形砖块拼成了一个大矩形,若大矩形的一边长为75cm,则小矩形砖块的面积为 cm2.
16.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为 mm2.
17.把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放,则图②中的大长方形纸片未被4个小长方形纸片覆盖部分的面积为 cm2.
18.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是 cm2.
三、解答题
19.如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形.求大长方形的面积.
20.列二元一次方程组解实际问题.
某纸制品厂要制作如图所示的甲,乙两种无盖的长方体盒子,该厂利用边角余料裁出了长方形,正方形两种纸片,其中长方形的宽与正方形的边长相等,现将105张正方形纸片和270张长方形纸片用来制作这两种盒子(不计连接部分).求可以恰好制作这两种盒子多少个?
21.学校征集校园便道地砖铺设的图形设计,小致用学校提供的若干个完全相同的小长方形模具(如图①)拼出一个大长方形和一个正方形(如图②、图③),其中所拼正方形中间留下一个边长为3cm小正方形的空间,求一个小长方形模具的面积.
22.二元一次方程组解应用题:
某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?
23.小明是一个乐思好问的学生,在解答七年级下册教材中一道拓广探索题时遇到了困难.这道题是这样的:
一个长方形的长减少5cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
(1)如图,设长方形的长、宽各是xcm,ycm,小明绞尽脑汁列出了三个不同的方程组:
①,②,③
以上三个方程组中,能正确反映题意的有 .(请直接填写序号)
(2)小明列出的方程,根据目前知识不易求解,便请教老师,老师提示这个问题可以列二元一次方程组来解答,并适时点拨,小明终于明白了.请你写出小明列出的二元一次方程组,并写出解题过程.
24.某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是200cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图甲所示,(单位:cm).
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将25张标准板材用裁法一裁剪,将5张标准板材用裁法二裁剪,再将得到的A型与B型板材分别做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?
答案
一、选择题
1.C.2.D.3.D.4.B.5.C.6.C.7.A.8.B.9.D.10.C.
二、填空题
11.79.
12.8.
13.300cm2.
14.76cm.
15.675.
16.375.
17.24.
18.3.
三、解答题
19.设小长方形的长为x,宽为y,
依题意,得:,
解得:,
∴S大长方形=2x (x+y)=2×10×(10+4)=280.
答:大长方形的面积为280.
20.设可以恰好制作x个甲种盒子,y个乙种盒子,
依题意,得:,
解得:.
答:可以恰好制作45个甲种盒子,30个乙种盒子.
21.根据题意得:,
解得:,
∴一个小长方形模具的面积=ab=15×9=135.
22.设小长方形的长为x米,宽为y米,
依题意,得:,
解得:,
∴210×2x×(x+2y)=75600(元).
答:要完成这块绿化工程,预计花费75600元.
23.(1)解:由题意得:.
故答案为:①②③
(2)设长方形的长、宽各是x cm,y cm,由题意列方程组,
得
解这个方程组,得
答:长方形的长、宽分别是cm、cm.
24.(1)依题意得:,
解得:.
答:图中的a=50,b=40.
(2)设可以做竖式无盖礼品盒x个,横式无盖礼品盒y个,
依题意得:,
解得:.
答:可以做竖式无盖礼品盒8个,横式无盖礼品盒16个.
一、选择题.
1.如图,在大长方形ABCD中,放入六个相同的小长方形,则阴影部分的面积为( )
A.140 cm2 B.96cm2 C.44 cm2 D.16 cm2
2.八块相同的长方形地砖拼成一个长方形,每块长方形地砖的宽等于( )
A.15cm B.30cm C.12cm D.10cm
3.如图,在大长方形中放入6个形状、大小相同的小长方形,所标尺寸如图所示,则图中大长方形的面积是( )
A.96 B.112 C.126 D.140
4.小林去超市帮妈妈买回一批规格一样的纸杯.如图,他把3个纸杯叠在一起高度是9cm,把8个纸杯叠在一起高度是14cm,若把50个纸杯叠在一起时,它的高度约是( )cm.
A.150cm B.56cm C.57cm D.81cm
5.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为110cm,此时木桶中水的深度是( )
A.60cm B.50cm C.40cm D.30cm
6.小明在拼图时,发现8个大小一样的小长方形恰好可以拼成一个大的长方形,如图1所示.小红看见了,说“我来试一试”,结果拼成如图2所示的正方形,中间还留有一个洞,恰好是边长为2cm的小正方形.则每个小长方形的长和宽分别为( )
A.8cm和6cm B.12cm和8cm C.10cm和6cm D.10cm和8cm
7.用如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒.现有m张正方形纸板和n张长方形纸板,如果做两种纸盒若干个,恰好将纸板用完,则m+n的值可能是( )
A.200 B.201 C.202 D.203
8.现有如图(1)的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图(2)的全等图形和8个如图(1)的小长方形,拼成如图(3)的大长方形,若大长方形的宽为30cm,则图(3)中阴影部分面积与整个图形的面积之比为( )
A. B. C. D.
9.如图,10块相同的小长方形墙砖拼成一个大长方形,设小长方形墙砖的长和宽分别为xcm和ycm,则两个小长方形的面积是( )
A.1200 B.1600 C.1800 D.2400
10.如图,是由7块颜色不同的正方形组成的长方形,已知中间小正方形的边长为1,这个长方形的面积为( )
A.45 B.48 C.63 D.64
二、填空题
11.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
12.如图,三个一样大小的小长方形沿“横﹣竖﹣横”排列在一个长为10,宽为8的大长方形中,则图中一个小长方形的面积等于 .
13.如图所示,8个相同的长方形地砖拼成一个大长方形,则每块小长方形地砖的面积是 .
14.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是 .
15.如图,汪曾祺纪念馆中的仿古墙独具特色,其中一处是由10块相同的小矩形砖块拼成了一个大矩形,若大矩形的一边长为75cm,则小矩形砖块的面积为 cm2.
16.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为 mm2.
17.把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放,则图②中的大长方形纸片未被4个小长方形纸片覆盖部分的面积为 cm2.
18.五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是 cm2.
三、解答题
19.如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形.求大长方形的面积.
20.列二元一次方程组解实际问题.
某纸制品厂要制作如图所示的甲,乙两种无盖的长方体盒子,该厂利用边角余料裁出了长方形,正方形两种纸片,其中长方形的宽与正方形的边长相等,现将105张正方形纸片和270张长方形纸片用来制作这两种盒子(不计连接部分).求可以恰好制作这两种盒子多少个?
21.学校征集校园便道地砖铺设的图形设计,小致用学校提供的若干个完全相同的小长方形模具(如图①)拼出一个大长方形和一个正方形(如图②、图③),其中所拼正方形中间留下一个边长为3cm小正方形的空间,求一个小长方形模具的面积.
22.二元一次方程组解应用题:
某居民小区为了绿化小区环境,建设和谐家园.准备将一块周长为76米的长方形空地,设计成长和宽分别相等的9块小长方形,如图所示.计划在空地上种上各种花卉,经市场预测,绿化每平方米空地造价210元,请计算,要完成这块绿化工程,预计花费多少元?
23.小明是一个乐思好问的学生,在解答七年级下册教材中一道拓广探索题时遇到了困难.这道题是这样的:
一个长方形的长减少5cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
(1)如图,设长方形的长、宽各是xcm,ycm,小明绞尽脑汁列出了三个不同的方程组:
①,②,③
以上三个方程组中,能正确反映题意的有 .(请直接填写序号)
(2)小明列出的方程,根据目前知识不易求解,便请教老师,老师提示这个问题可以列二元一次方程组来解答,并适时点拨,小明终于明白了.请你写出小明列出的二元一次方程组,并写出解题过程.
24.某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是200cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图甲所示,(单位:cm).
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将25张标准板材用裁法一裁剪,将5张标准板材用裁法二裁剪,再将得到的A型与B型板材分别做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?
答案
一、选择题
1.C.2.D.3.D.4.B.5.C.6.C.7.A.8.B.9.D.10.C.
二、填空题
11.79.
12.8.
13.300cm2.
14.76cm.
15.675.
16.375.
17.24.
18.3.
三、解答题
19.设小长方形的长为x,宽为y,
依题意,得:,
解得:,
∴S大长方形=2x (x+y)=2×10×(10+4)=280.
答:大长方形的面积为280.
20.设可以恰好制作x个甲种盒子,y个乙种盒子,
依题意,得:,
解得:.
答:可以恰好制作45个甲种盒子,30个乙种盒子.
21.根据题意得:,
解得:,
∴一个小长方形模具的面积=ab=15×9=135.
22.设小长方形的长为x米,宽为y米,
依题意,得:,
解得:,
∴210×2x×(x+2y)=75600(元).
答:要完成这块绿化工程,预计花费75600元.
23.(1)解:由题意得:.
故答案为:①②③
(2)设长方形的长、宽各是x cm,y cm,由题意列方程组,
得
解这个方程组,得
答:长方形的长、宽分别是cm、cm.
24.(1)依题意得:,
解得:.
答:图中的a=50,b=40.
(2)设可以做竖式无盖礼品盒x个,横式无盖礼品盒y个,
依题意得:,
解得:.
答:可以做竖式无盖礼品盒8个,横式无盖礼品盒16个.
