人教版九年级数学上册 22.3 实际问题与二次函数 最大利润问题 课件 2022--2023学年(共32张PPT)
文档属性
| 名称 | 人教版九年级数学上册 22.3 实际问题与二次函数 最大利润问题 课件 2022--2023学年(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 13:46:13 | ||
图片预览










文档简介
(共32张PPT)
人教版 数学 九年级 上册
22.3 实际问题与二次函数
第2课时 最大利润问题
学习目标
素养目标
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.(重点)
2.弄清商品销售问题中的数量关系及确定自变量的取值范围. (难点)
知识回顾
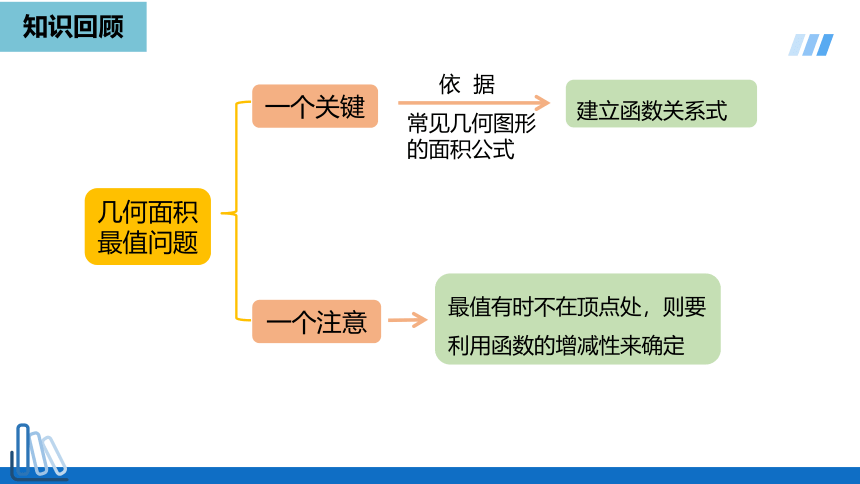
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
例1.某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=-2x+180.为保证市场稳定,供货商规定销售价格不得低于75元/件且不得高于90元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式;
(2)每件小电器的销售价格定为多少元时,才能使每天获得的利润最大,最大是多少元?
解:(1)由题意可得w=(x-45-5)(-2x+180)=-2x2+280x-9000
(2)w=-2x2+280x-9000=-2(x-70)2+800
∵ 销售价格不得低于75元/件且不得高于90元/件
∴ 75≤x≤90
∵ -2<0,∴ 当75≤x≤90时,w随x的增大而减小
∴ 当x=75时,有最大利润,最大利润为750元
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件. 那么,涨价多少元时,一个月内利润最大,最大利润是多少?
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,根据题意,得
y=(30-20+x)(180-10x)
即:y=-10x2+80x+1800=-10(x-4)2+1960
∵ -10<0,∴ 当x=4时,y取最大值1960元
答:涨价4元时,一个月内利润最大,最大利润为1960元.
知识点1
新知探究
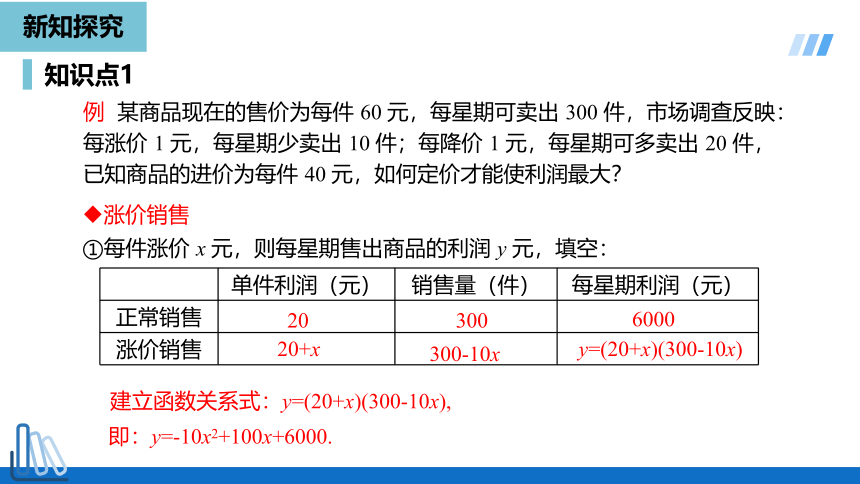
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出 10 件;每降价 1 元,每星期可多卖出 20 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?
涨价销售
①每件涨价 x 元,则每星期售出商品的利润 y 元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
知识点1
新知探究
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价 65 元时,最大利润是 6250 元.
知识点1
新知探究
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出 10 件;每降价 1 元,每星期可多卖出 20 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?
知识点1
新知探究
综合涨价和降价两种情况可知,定价 65 元时,利润最大.
②自变量 x 的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且 x ≥0,因此自变量的取值范围是 0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
当x= - =2.5 时, y= - 20×(2.5) 2+100×2.5+6000=6125
即定价 57.5 元时,最大利润是 6125元.
即:y= -20x2+100x+6000,
(2)降价情况下,定价57.5元时,有最大利润6125元.
(1)涨价情况下,定价65元时,有最大利润6250元.
综上可知:
该商品的价格定价为65元时,可获得最大利润6250元.
知识点1
新知探究
求解最大利润问题时,要熟练掌握利润问题中相关数量的意义以及常用的数量关系.审清题意,根据具体问题,建立函数关系式,解决实际问题.
常见的销售问题中的数量关系:利润=售价-成本,总利润=每件商品的利润×销量,利润率=×100%.
方法点拨
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式法求出最大利润;也可以画出函数的简图,利用简图和性质求出.
探究新知
跟踪训练
新知探究
某青年公寓有 100 张床位,每张床位的日租价为 10 元时,公寓的床位可全部出租.若每张床位的日租价提高 1 元,则租出的床位就会减少 5 张,按此种情况,要想获得最大收益,则每张床位的日租价需提高 元.
5
解:设每张床位的日租价提高x元,总收益为y元.
则y=(10+x)(100-5x) =-5(x-5)2 +1125.
所以当x=5时,总收益y取得最大值1125.
故每张床位的日租价需提高5元,才能获得最大收益.
随堂练习
1
为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业.王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价 x (元)和游客居住房间数 y (间)的信息,乐乐绘制出 y 与 x 的函数图象如图所示.
(1)求 y 与 x 之间的函数关系式;
解:(1) 设y与x之间的函数关系式为y=kx+b(k≠0),
根据题意得解得
故y与x之间的函数关系式是y=-0.5x+110.
随堂练习
1
(2) 设合作社每天获得的利润为w元,
则w=x(-0.5x+110)-20(-0.5x+ 110) =-0.5x2+120x-2 200=-0.5(x-120)2+5000,
因为60≤x≤150,
所以当x=120时,w取得最大值,此时w=5000,
故当房价定为120元时,合作社每天获利最大,最大利润是5000元.
(2)合作社规定每个房间价格不低于 60 元且不超过 150 元,对于游客所居住的每个房间,合作社每天需要支出 20 元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
随堂练习
2
某种商品每件的进价为 30 元,在某段时间内若以每件 x 元出售,可卖出(100-x) 件,应该如何定价才能使利润最大?
解:设最大利润为w元
则w=(x-30)(100-x)=-(x-65)2+1225,
∵30≤x≤100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
随堂练习
3
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,销售价格每上涨1元,每天的销售量就减少10件.
(1) 请你写出商场销售这种文具,每天所得的销售利润w元与销售价格x元/件之间的函数关系式;
(2) 销售价格为多少时,每天的销售利润最大?
解:(1) w=(x -20)[250-10(x-25)]=-10x2 +700x-10000.
(2) w=-10x2+700x-10000=-10(x-35) 2 +2250,
故当x=35时,w有最大值2250.
即销售价格为35元/件时,每天的销售利润最大.
随堂练习
3
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,销售价格每上涨1元,每天的销售量就减少10件.
(3) 商场的营销部结合上述情况,提出了A,B两种营销方案.
方案A:该文具的销售价格高于进价且不超过30元/件;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请通过计算说明哪种方案的最大利润更高.
随堂练习
3
解:(3)方案A:由题意得w=-10(x-35)2+ 2250(20因为-10<0,抛物线的对称轴为直线x=35,
所以抛物线开口向下,在对称轴的左侧,w随x的增大而增大,
所以当x=30时,w取最大值2000.
方案B:由题意得解得45≤ x ≤49.
由题意得w=-10(x-35)2 +2250(45≤ x ≤49).
因为在对称轴(直线 x =35)的右侧,w随x的增大而减小,
所以当x=45时,w有最大值1250.
因为2000> 1250,所以方案A的最大利润更高.
课堂小结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式法求最大值或利用函数简图和性质求出.
对接中考
1
某种商品每件进价为 20 元,调查表明:在某段时间内,若以每件 x 元(20≤x≤30,且 x 为整数)出售,可卖出(30-x) 件,若利润最大,每件的售价应为 元.
25
解:设利润为w元,
则w=(x-20)(30-x)=-(x-25)2+25,
∵20≤x≤30,
∴当x=25时,二次函数有最大值25.
对接中考
2
旅游公司在景区内配置了 50 辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金 x(元)是 5 的倍数.发现每天的营运规律如下:当 x 不超过100 元时,观光车能全部租出;当 x 超过100 元时,每辆车的日租金每增加 5 元,租出去的观光车就会减少 1 辆.已知所有观光车每天的管理费是1100元.
(1)为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?
解:(1) 由题意知,若观光车能全部租出,则0<x≤100,
由50x-1100>0,解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元.
对接中考
2
旅游公司在景区内配置了 50 辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金 x(元)是 5 的倍数.发现每天的营运规律如下:当 x 不超过100 元时,观光车能全部租出;当 x 超过100 元时,每辆车的日租金每增加 5 元,租出去的观光车就会减少 1 辆.已知所有观光车每天的管理费是1100元.
(2)当每辆车的日租金为多少元时,每天的净收入最多?
解:(2)设每天的净收入为y元,当0<x≤100时,y=50x-1100,
∵y随x的增大而增大,∴当x=100时,y的最大值为50×100-1100=3900;
当x>100时,y=(50-)x-1100=-x2+70x-1100=-(x-175)2+5025,
当x=175时,y的最大值为5025,
∵5025>3900,故当每辆车的日租金为175元时,每天的净收入最多.
某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价提高多少元时,才能在半个月内获得最大利润
解:设售价提高x元时,半月内获得的利润为y元.则
y=(x+30-20)(400-20x)
=-20x2+200x+4000
=-20(x-5)2+4500.
∴当x=5时,y最大 =4500 .
答:当售价提高5元时,半月内可获最大利润4500元.
巩固练习
变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:Q与x的函数关系式为:
60x-1800 , (40≤x≤50 )
-2(x-55)2 + 1250. (50≤x≤70)
Q =
由例3可知:
若40≤x≤50, 则当x=50时,Q最大= 1200,
若50≤x≤70, 则当x=55时,Q最大= 1250.
∵1200<1250
∴售价x是55元时,获利最大,最大利润是1250元.
探究新知
(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,∵Q最大= 1200<1218,
∴此情况不存在.
60x-1800 , (40≤x≤50 )
-2(x-55)2 + 1250. (50≤x≤70)
Q =
探究新知
②当50≤x≤70时, Q最大= 1250>1218,
令Q = 1218,得-2(x-55)2 +1250=1218.
解得x1=51,x2=59.
由Q = -2(x-55)2 +1250的图象和性质可知:
当51≤x≤59时,Q≥1218.
因此若该商品所获利润不低于1218元,
则售价x的取值范围为51≤x≤59.
x
Q
0
55
1218
59
51
1250
(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得
51≤x≤59,
30 (-2 x +160)≥1620.
解得:51≤x≤53.
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,Q随x的增大而增大.
∴当x最大 = 53时,Q最大= 1242.
∴此时售价x应定为53元,利润最大,最大利润是1242元.
x
Q
o
55
1242
53
51
探究新知
随堂演练
1.下列抛物线有最高点或最低点吗?如果有,写出这些点的坐标(用公式):
(1)y=-4x2+3x; (2)y=3x2+x+6.
2.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应如何定价才能使利润最大?
解:设所得利润为y元,
由题意得y=x(200-x)-30(200-x)
=-x2+230x-6000
=-(x-115)2+7225 (0当x=115时,y有最大值.
即当这件商品定价为115元时,利润最大.
综合应用
3.某种文化衫以每件盈利20元的价格出售,每天可售出40件. 若每件降价1元,则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440 (0<x<20).
当x=8时,y取最大值1440.
即当每件降价8元时,每天的盈利最多。
拓展延伸
4.求函数y=-x2+6x+5的最大值和最小值.
(1)0≤x≤6; (2) -2≤x≤2.
解:y=-x2+6x+5=-(x-3)2+14
(1)当0≤x≤6时,
当x=3时, y有最大值14,
当x=0或6时,y有最小值5.
(2)当-2≤x≤2时,
当x=2时,y有最大值13,
当x=-2时,y有最小值-11.
人教版 数学 九年级 上册
22.3 实际问题与二次函数
第2课时 最大利润问题
学习目标
素养目标
1.能应用二次函数的性质解决商品销售过程中的最大利润问题.(重点)
2.弄清商品销售问题中的数量关系及确定自变量的取值范围. (难点)
知识回顾
几何面积最值问题
一个关键
一个注意
建立函数关系式
常见几何图形的面积公式
依 据
最值有时不在顶点处,则要利用函数的增减性来确定
例1.某电商在购物平台上销售一款小电器,其进价为45元/件,每销售一件需缴纳平台推广费5元,该款小电器每天的销售量y(件)与每件的销售价格x(元)满足函数关系:y=-2x+180.为保证市场稳定,供货商规定销售价格不得低于75元/件且不得高于90元/件.
(1)写出每天的销售利润w(元)与销售价格x(元)的函数关系式;
(2)每件小电器的销售价格定为多少元时,才能使每天获得的利润最大,最大是多少元?
解:(1)由题意可得w=(x-45-5)(-2x+180)=-2x2+280x-9000
(2)w=-2x2+280x-9000=-2(x-70)2+800
∵ 销售价格不得低于75元/件且不得高于90元/件
∴ 75≤x≤90
∵ -2<0,∴ 当75≤x≤90时,w随x的增大而减小
∴ 当x=75时,有最大利润,最大利润为750元
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件. 那么,涨价多少元时,一个月内利润最大,最大利润是多少?
解:设每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,根据题意,得
y=(30-20+x)(180-10x)
即:y=-10x2+80x+1800=-10(x-4)2+1960
∵ -10<0,∴ 当x=4时,y取最大值1960元
答:涨价4元时,一个月内利润最大,最大利润为1960元.
知识点1
新知探究
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出 10 件;每降价 1 元,每星期可多卖出 20 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?
涨价销售
①每件涨价 x 元,则每星期售出商品的利润 y 元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
知识点1
新知探究
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价 65 元时,最大利润是 6250 元.
知识点1
新知探究
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
单件利润(元) 销售量(件) 每星期利润(元)
正常销售
降价销售
20
300
20-x
300+20x
y=(20-x)(300+20x)
建立函数关系式:y=(20-x)(300+20x),
即:y=-20x2+100x+6000.
6000
例 某商品现在的售价为每件 60 元,每星期可卖出 300 件,市场调查反映:每涨价 1 元,每星期少卖出 10 件;每降价 1 元,每星期可多卖出 20 件,已知商品的进价为每件 40 元,如何定价才能使利润最大?
知识点1
新知探究
综合涨价和降价两种情况可知,定价 65 元时,利润最大.
②自变量 x 的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且 x ≥0,因此自变量的取值范围是 0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
当x= - =2.5 时, y= - 20×(2.5) 2+100×2.5+6000=6125
即定价 57.5 元时,最大利润是 6125元.
即:y= -20x2+100x+6000,
(2)降价情况下,定价57.5元时,有最大利润6125元.
(1)涨价情况下,定价65元时,有最大利润6250元.
综上可知:
该商品的价格定价为65元时,可获得最大利润6250元.
知识点1
新知探究
求解最大利润问题时,要熟练掌握利润问题中相关数量的意义以及常用的数量关系.审清题意,根据具体问题,建立函数关系式,解决实际问题.
常见的销售问题中的数量关系:利润=售价-成本,总利润=每件商品的利润×销量,利润率=×100%.
方法点拨
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润:
可以利用配方法或公式法求出最大利润;也可以画出函数的简图,利用简图和性质求出.
探究新知
跟踪训练
新知探究
某青年公寓有 100 张床位,每张床位的日租价为 10 元时,公寓的床位可全部出租.若每张床位的日租价提高 1 元,则租出的床位就会减少 5 张,按此种情况,要想获得最大收益,则每张床位的日租价需提高 元.
5
解:设每张床位的日租价提高x元,总收益为y元.
则y=(10+x)(100-5x) =-5(x-5)2 +1125.
所以当x=5时,总收益y取得最大值1125.
故每张床位的日租价需提高5元,才能获得最大收益.
随堂练习
1
为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业.王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价 x (元)和游客居住房间数 y (间)的信息,乐乐绘制出 y 与 x 的函数图象如图所示.
(1)求 y 与 x 之间的函数关系式;
解:(1) 设y与x之间的函数关系式为y=kx+b(k≠0),
根据题意得解得
故y与x之间的函数关系式是y=-0.5x+110.
随堂练习
1
(2) 设合作社每天获得的利润为w元,
则w=x(-0.5x+110)-20(-0.5x+ 110) =-0.5x2+120x-2 200=-0.5(x-120)2+5000,
因为60≤x≤150,
所以当x=120时,w取得最大值,此时w=5000,
故当房价定为120元时,合作社每天获利最大,最大利润是5000元.
(2)合作社规定每个房间价格不低于 60 元且不超过 150 元,对于游客所居住的每个房间,合作社每天需要支出 20 元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
随堂练习
2
某种商品每件的进价为 30 元,在某段时间内若以每件 x 元出售,可卖出(100-x) 件,应该如何定价才能使利润最大?
解:设最大利润为w元
则w=(x-30)(100-x)=-(x-65)2+1225,
∵30≤x≤100,
∴当x=65时,二次函数有最大值1225,
∴定价是65元时,利润最大.
随堂练习
3
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,销售价格每上涨1元,每天的销售量就减少10件.
(1) 请你写出商场销售这种文具,每天所得的销售利润w元与销售价格x元/件之间的函数关系式;
(2) 销售价格为多少时,每天的销售利润最大?
解:(1) w=(x -20)[250-10(x-25)]=-10x2 +700x-10000.
(2) w=-10x2+700x-10000=-10(x-35) 2 +2250,
故当x=35时,w有最大值2250.
即销售价格为35元/件时,每天的销售利润最大.
随堂练习
3
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,销售价格每上涨1元,每天的销售量就减少10件.
(3) 商场的营销部结合上述情况,提出了A,B两种营销方案.
方案A:该文具的销售价格高于进价且不超过30元/件;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请通过计算说明哪种方案的最大利润更高.
随堂练习
3
解:(3)方案A:由题意得w=-10(x-35)2+ 2250(20
所以抛物线开口向下,在对称轴的左侧,w随x的增大而增大,
所以当x=30时,w取最大值2000.
方案B:由题意得解得45≤ x ≤49.
由题意得w=-10(x-35)2 +2250(45≤ x ≤49).
因为在对称轴(直线 x =35)的右侧,w随x的增大而减小,
所以当x=45时,w有最大值1250.
因为2000> 1250,所以方案A的最大利润更高.
课堂小结
最大利润问题
建立函数关系式
总利润=单件利润×销售量或总利润=总售价-总成本.
确定自变量取值范围
涨价:要保证销售量≥0;
降价:要保证单件利润≥0.
确定最大利润
利用配方法或公式法求最大值或利用函数简图和性质求出.
对接中考
1
某种商品每件进价为 20 元,调查表明:在某段时间内,若以每件 x 元(20≤x≤30,且 x 为整数)出售,可卖出(30-x) 件,若利润最大,每件的售价应为 元.
25
解:设利润为w元,
则w=(x-20)(30-x)=-(x-25)2+25,
∵20≤x≤30,
∴当x=25时,二次函数有最大值25.
对接中考
2
旅游公司在景区内配置了 50 辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金 x(元)是 5 的倍数.发现每天的营运规律如下:当 x 不超过100 元时,观光车能全部租出;当 x 超过100 元时,每辆车的日租金每增加 5 元,租出去的观光车就会减少 1 辆.已知所有观光车每天的管理费是1100元.
(1)为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?
解:(1) 由题意知,若观光车能全部租出,则0<x≤100,
由50x-1100>0,解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元.
对接中考
2
旅游公司在景区内配置了 50 辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金 x(元)是 5 的倍数.发现每天的营运规律如下:当 x 不超过100 元时,观光车能全部租出;当 x 超过100 元时,每辆车的日租金每增加 5 元,租出去的观光车就会减少 1 辆.已知所有观光车每天的管理费是1100元.
(2)当每辆车的日租金为多少元时,每天的净收入最多?
解:(2)设每天的净收入为y元,当0<x≤100时,y=50x-1100,
∵y随x的增大而增大,∴当x=100时,y的最大值为50×100-1100=3900;
当x>100时,y=(50-)x-1100=-x2+70x-1100=-(x-175)2+5025,
当x=175时,y的最大值为5025,
∵5025>3900,故当每辆车的日租金为175元时,每天的净收入最多.
某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价提高多少元时,才能在半个月内获得最大利润
解:设售价提高x元时,半月内获得的利润为y元.则
y=(x+30-20)(400-20x)
=-20x2+200x+4000
=-20(x-5)2+4500.
∴当x=5时,y最大 =4500 .
答:当售价提高5元时,半月内可获最大利润4500元.
巩固练习
变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:Q与x的函数关系式为:
60x-1800 , (40≤x≤50 )
-2(x-55)2 + 1250. (50≤x≤70)
Q =
由例3可知:
若40≤x≤50, 则当x=50时,Q最大= 1200,
若50≤x≤70, 则当x=55时,Q最大= 1250.
∵1200<1250
∴售价x是55元时,获利最大,最大利润是1250元.
探究新知
(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,∵Q最大= 1200<1218,
∴此情况不存在.
60x-1800 , (40≤x≤50 )
-2(x-55)2 + 1250. (50≤x≤70)
Q =
探究新知
②当50≤x≤70时, Q最大= 1250>1218,
令Q = 1218,得-2(x-55)2 +1250=1218.
解得x1=51,x2=59.
由Q = -2(x-55)2 +1250的图象和性质可知:
当51≤x≤59时,Q≥1218.
因此若该商品所获利润不低于1218元,
则售价x的取值范围为51≤x≤59.
x
Q
0
55
1218
59
51
1250
(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得
51≤x≤59,
30 (-2 x +160)≥1620.
解得:51≤x≤53.
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,Q随x的增大而增大.
∴当x最大 = 53时,Q最大= 1242.
∴此时售价x应定为53元,利润最大,最大利润是1242元.
x
Q
o
55
1242
53
51
探究新知
随堂演练
1.下列抛物线有最高点或最低点吗?如果有,写出这些点的坐标(用公式):
(1)y=-4x2+3x; (2)y=3x2+x+6.
2.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应如何定价才能使利润最大?
解:设所得利润为y元,
由题意得y=x(200-x)-30(200-x)
=-x2+230x-6000
=-(x-115)2+7225 (0
即当这件商品定价为115元时,利润最大.
综合应用
3.某种文化衫以每件盈利20元的价格出售,每天可售出40件. 若每件降价1元,则每天可多售10件,如果每天要盈利最多,每件应降价多少元?
解:设每件应降价x元,每天的利润为y元,
由题意得:y=(20-x)(40+10x)
=-10x2+160x+800
=-10(x-8)2+1440 (0<x<20).
当x=8时,y取最大值1440.
即当每件降价8元时,每天的盈利最多。
拓展延伸
4.求函数y=-x2+6x+5的最大值和最小值.
(1)0≤x≤6; (2) -2≤x≤2.
解:y=-x2+6x+5=-(x-3)2+14
(1)当0≤x≤6时,
当x=3时, y有最大值14,
当x=0或6时,y有最小值5.
(2)当-2≤x≤2时,
当x=2时,y有最大值13,
当x=-2时,y有最小值-11.
同课章节目录
