苏科版八年级上册3.3 勾股定理的简单应用 课件 (共16张PPT)
文档属性
| 名称 | 苏科版八年级上册3.3 勾股定理的简单应用 课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 653.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 16:37:03 | ||
图片预览






文档简介
(共16张PPT)
八年级(上册)
初中数学
3.3 勾股定理的简单应用
交流
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
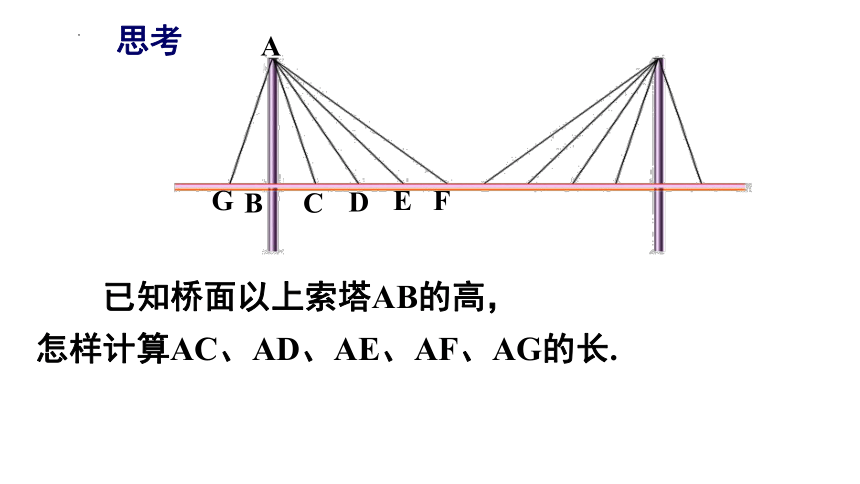
思考
已知桥面以上索塔AB的高,
怎样计算AC、AD、AE、AF、AG的长.
A
B
C
E
F
G
D
例1 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
自主探究
意思是:有一根竹子原高1丈(1丈=10尺), 中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高
A
O
B
x
(10-x)
3
例1 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
自主探究
A
O
B
x
(10-x)
3
解:如图,
设OA=x,则AB=10-x.
∵∠AOB= 90°,
∴OA2+OB2 = AB2,
∴x2+32 = (10-x)2.
解得:x = 4.55
答:折断处离地面有4.55尺.
题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少
“引葭(jiā)赴岸”是《九章算术》中另一道题: “今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何 ”
A
C
B
x+1
5
x
自主合作
解:如图,
BC为芦苇长,AB为水深,AC为池中心点距岸边的距离.
设AB=x尺,则BC =(x+1)尺,
根据勾股定理得:x2+52=(x+1)2,
即:(x+1)2-x2 =52,
解得:x=12,
所以芦苇长为12+1=13(尺),
答:水深为12尺,芦苇长为13尺.
A
C
B
x+1
5
x
例2 如图,AD是△ABC的中线,AD=24,AB=26,
BC=20,求AC.
D
C
B
A
自主探究
1.如图, 计算四边形ABCD的面积.
自主展示
D
C
B
A
∟
15
12
16
25
2.一个三角形三边长的比为3:4:5,它的周长是60cm,求这个三角形的面积.
3.如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积.
D
C
B
A
∟
自主展示
3.如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积.
自主展示
变式:
D
C
B
A
∟
D
C
B
A
∟
如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状.
自主拓展
A
B
C
议一议
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系;把研究等腰三角形转化为研究直角三角形,这是研究问题的一种策略.
自主评价
已知:如图,△ABC中,AB=AC=10,BC=16,
点D在BC上,DA⊥CA于点A.
求BD的长.
A
B
C
D
∟
E
∟
思考题
说一说
你的收获!
八年级(上册)
初中数学
3.3 勾股定理的简单应用
交流
从远处看,斜拉桥的索塔、桥面与拉索组成许多直角三角形.
思考
已知桥面以上索塔AB的高,
怎样计算AC、AD、AE、AF、AG的长.
A
B
C
E
F
G
D
例1 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
自主探究
意思是:有一根竹子原高1丈(1丈=10尺), 中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高
A
O
B
x
(10-x)
3
例1 九章算术中的“折竹”问题:
今有竹高一丈,末折抵地,去根三尺,问折者高几何
自主探究
A
O
B
x
(10-x)
3
解:如图,
设OA=x,则AB=10-x.
∵∠AOB= 90°,
∴OA2+OB2 = AB2,
∴x2+32 = (10-x)2.
解得:x = 4.55
答:折断处离地面有4.55尺.
题意是:有一个边长为10尺的正方形池塘,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好到达岸边.请问这个水池的深度和这根芦苇的长度各是多少
“引葭(jiā)赴岸”是《九章算术》中另一道题: “今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何 ”
A
C
B
x+1
5
x
自主合作
解:如图,
BC为芦苇长,AB为水深,AC为池中心点距岸边的距离.
设AB=x尺,则BC =(x+1)尺,
根据勾股定理得:x2+52=(x+1)2,
即:(x+1)2-x2 =52,
解得:x=12,
所以芦苇长为12+1=13(尺),
答:水深为12尺,芦苇长为13尺.
A
C
B
x+1
5
x
例2 如图,AD是△ABC的中线,AD=24,AB=26,
BC=20,求AC.
D
C
B
A
自主探究
1.如图, 计算四边形ABCD的面积.
自主展示
D
C
B
A
∟
15
12
16
25
2.一个三角形三边长的比为3:4:5,它的周长是60cm,求这个三角形的面积.
3.如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积.
D
C
B
A
∟
自主展示
3.如图, 在△ABC中, AB=15, AC=13, AD是BC上的高, AD=12, 求△ABC的周长和面积.
自主展示
变式:
D
C
B
A
∟
D
C
B
A
∟
如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状.
自主拓展
A
B
C
议一议
勾股定理与它的逆定理在应用上有什么区别?
勾股定理主要应用于求线段的长度、图形的周长、面积;
勾股定理的逆定理用于判断三角形的形状.
从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系;把研究等腰三角形转化为研究直角三角形,这是研究问题的一种策略.
自主评价
已知:如图,△ABC中,AB=AC=10,BC=16,
点D在BC上,DA⊥CA于点A.
求BD的长.
A
B
C
D
∟
E
∟
思考题
说一说
你的收获!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
