第1讲+认识圆和圆的周长(课件)六年级上册数学北师大版(共22张PPT)
文档属性
| 名称 | 第1讲+认识圆和圆的周长(课件)六年级上册数学北师大版(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 16:35:00 | ||
图片预览








文档简介
(共22张PPT)
开学第一课
敏思笃行 唯实求真
让学习变得像呼吸一样简单
20m
20m
认识圆和圆的周长
各部分名称
圆的特征
圆的对称性
圆
的
认
识
知识框架
圆的周长
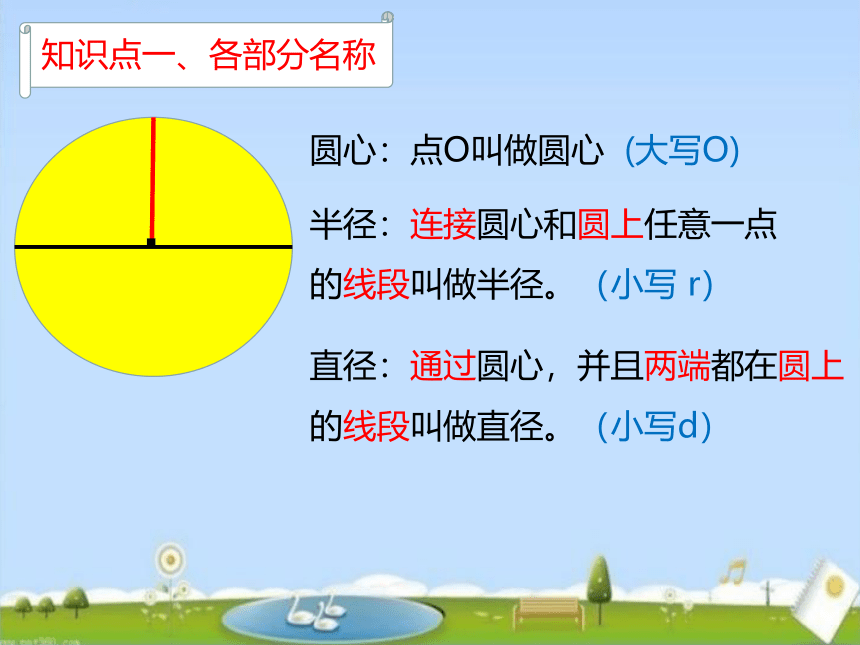
知识点一、各部分名称
.
圆心:点O叫做圆心 (大写O)
半径:连接圆心和圆上任意一点 的线段叫做半径。(小写 r)
直径:通过圆心,并且两端都在圆上的线段叫做直径。(小写d)
典型例题一
判断题:
1、圆规两脚间的距离是6cm,画出的圆的直径是6cm。
2、通过圆心的线段都是直径。
同一个圆中,直径是半径的2倍,d=2r 或r= d
圆心确定圆的位置;半径(或直径)决定圆的大小。
圆
有无数条直径、无数条半径
同一个圆中的直径都相等,半径都相等
知识点二、圆的特征
圆的特征
典型例题二
判断题:
1、所有的半径都相等,所有的直径都相等。
2、直径是半径的2倍,即d=2r 或 r= d
3、圆心确定圆的位置,半径决定圆的大小。
知识点三、圆的对称性
圆是轴对称图形,直径所在的直线是圆的对称轴,所以圆有无数条对称轴。
典型例题三
1、半圆有( )条对称轴,圆有( )条对称轴。
2、画出下面图形的对称轴。
3条
1条
1条
1
无数
无
敏思笃行 唯实求真
让学习变得像呼吸一样简单
知识点四、圆的周长
1、圆周率的意义:
圆的周长除以直径的商是一个固定的数,我们把它叫作圆周率,用字母 π 表示,通常取3.14。
敏思笃行 唯实求真
让学习变得像呼吸一样简单
已知半径(r) 已知直径(d) 已知周长 (C)
求半径(r)
求直径(d)
求周长(C)
r=d÷2
r=C÷π÷2
d=2r
C=2πr
C=πd
d=C÷π
知识点四、圆的周长
2、公 式
求半圆周长
C=πr+2r
典型例题四
(一)判断题
1、大小不同的两个圆,大圆的圆周率大,小圆的圆周率小。
2、π=3.14
3、一个圆的半径扩大到原来的2倍,则直径扩大到原来的4倍,周长扩大到原来的8倍。
2、一辆自行车车轮的直径是70cm,滚一圈有多远?滚100圈呢?
2×3.14×40=6.28×40=251.2(cm)
答:这根分针的尖端转动一周所走的路程是251.2厘米。
(二)应用题
1、候车室的墙壁上挂着一个大钟,它的分针长40cm,这根分针的尖端转动一周所走的路程是多少厘米?
3.14×70=219.8(cm) 219.8×100=21980(cm)
答:滚一圈有219.8厘米,滚100圈有21980厘米。
3、小丽量得下图圆桌的周长是4.71米,这个圆桌的直径是多少米?
4.71÷3.14=1.5(m)
答:这个圆桌的直径是1.5米。
4、世界上最高摩天轮的周长约是450米,它的半径是多少米?
(得数保留整数)
450÷3.14÷2≈72(m)
答:它的半径是72米。
6、一个世界上最粗的大树,树干直径达17.5m,多少个身高1.70m的成年人伸开双臂才能围住这棵大树?(保留整数)
17.5×3.14÷1.7=54.95÷1.7≈33(个)
答:多少个身高1.70m的成年人伸开双臂才能围住这棵大树。
5、一辆自行车外轮的直径是0.6m,如果它每分钟转200圈,要通过一座长753.6m的桥,需要多少分?
3.14×0.6×200=376.8(m)
753.6÷376.8=2(分)
答:要通过一座长753.6m的桥,需要2分钟。
7、一个半圆形苗圃的半径是4m,它的周长是多少米?
3.14×4+4×2=12.56+8=20.56(m)
答:它的周长是20.56米。
各部分名称
圆心:O(大写)
半径:连接圆心和圆上任意一点的线段叫做半径。r(小写)
直径:通过圆心,并且两端都在圆上的线段叫做直径。d(小写)
圆的特征
同一个圆中,直径是半径的2倍,d=2r 或r= d
圆心确定圆的位置;半径(或直径)决定圆的大小。
圆是轴对称图形,直径所在的直线是圆的对称轴,所以圆有无数条对称轴。
圆的对称性
圆
的
认
识
圆
有无数条直径、无数条半径
同一个圆中的直径都相等,半径都相等
圆的周长
C = πd 或 C = 2πr
能力提升
边
长
是
4
宽
2
长5
正方形内最大圆的直径长度等于正方形的边长。
长方形内最大圆的直径长度等于长方形的宽。
THE END
开学第一课
敏思笃行 唯实求真
让学习变得像呼吸一样简单
20m
20m
认识圆和圆的周长
各部分名称
圆的特征
圆的对称性
圆
的
认
识
知识框架
圆的周长
知识点一、各部分名称
.
圆心:点O叫做圆心 (大写O)
半径:连接圆心和圆上任意一点 的线段叫做半径。(小写 r)
直径:通过圆心,并且两端都在圆上的线段叫做直径。(小写d)
典型例题一
判断题:
1、圆规两脚间的距离是6cm,画出的圆的直径是6cm。
2、通过圆心的线段都是直径。
同一个圆中,直径是半径的2倍,d=2r 或r= d
圆心确定圆的位置;半径(或直径)决定圆的大小。
圆
有无数条直径、无数条半径
同一个圆中的直径都相等,半径都相等
知识点二、圆的特征
圆的特征
典型例题二
判断题:
1、所有的半径都相等,所有的直径都相等。
2、直径是半径的2倍,即d=2r 或 r= d
3、圆心确定圆的位置,半径决定圆的大小。
知识点三、圆的对称性
圆是轴对称图形,直径所在的直线是圆的对称轴,所以圆有无数条对称轴。
典型例题三
1、半圆有( )条对称轴,圆有( )条对称轴。
2、画出下面图形的对称轴。
3条
1条
1条
1
无数
无
敏思笃行 唯实求真
让学习变得像呼吸一样简单
知识点四、圆的周长
1、圆周率的意义:
圆的周长除以直径的商是一个固定的数,我们把它叫作圆周率,用字母 π 表示,通常取3.14。
敏思笃行 唯实求真
让学习变得像呼吸一样简单
已知半径(r) 已知直径(d) 已知周长 (C)
求半径(r)
求直径(d)
求周长(C)
r=d÷2
r=C÷π÷2
d=2r
C=2πr
C=πd
d=C÷π
知识点四、圆的周长
2、公 式
求半圆周长
C=πr+2r
典型例题四
(一)判断题
1、大小不同的两个圆,大圆的圆周率大,小圆的圆周率小。
2、π=3.14
3、一个圆的半径扩大到原来的2倍,则直径扩大到原来的4倍,周长扩大到原来的8倍。
2、一辆自行车车轮的直径是70cm,滚一圈有多远?滚100圈呢?
2×3.14×40=6.28×40=251.2(cm)
答:这根分针的尖端转动一周所走的路程是251.2厘米。
(二)应用题
1、候车室的墙壁上挂着一个大钟,它的分针长40cm,这根分针的尖端转动一周所走的路程是多少厘米?
3.14×70=219.8(cm) 219.8×100=21980(cm)
答:滚一圈有219.8厘米,滚100圈有21980厘米。
3、小丽量得下图圆桌的周长是4.71米,这个圆桌的直径是多少米?
4.71÷3.14=1.5(m)
答:这个圆桌的直径是1.5米。
4、世界上最高摩天轮的周长约是450米,它的半径是多少米?
(得数保留整数)
450÷3.14÷2≈72(m)
答:它的半径是72米。
6、一个世界上最粗的大树,树干直径达17.5m,多少个身高1.70m的成年人伸开双臂才能围住这棵大树?(保留整数)
17.5×3.14÷1.7=54.95÷1.7≈33(个)
答:多少个身高1.70m的成年人伸开双臂才能围住这棵大树。
5、一辆自行车外轮的直径是0.6m,如果它每分钟转200圈,要通过一座长753.6m的桥,需要多少分?
3.14×0.6×200=376.8(m)
753.6÷376.8=2(分)
答:要通过一座长753.6m的桥,需要2分钟。
7、一个半圆形苗圃的半径是4m,它的周长是多少米?
3.14×4+4×2=12.56+8=20.56(m)
答:它的周长是20.56米。
各部分名称
圆心:O(大写)
半径:连接圆心和圆上任意一点的线段叫做半径。r(小写)
直径:通过圆心,并且两端都在圆上的线段叫做直径。d(小写)
圆的特征
同一个圆中,直径是半径的2倍,d=2r 或r= d
圆心确定圆的位置;半径(或直径)决定圆的大小。
圆是轴对称图形,直径所在的直线是圆的对称轴,所以圆有无数条对称轴。
圆的对称性
圆
的
认
识
圆
有无数条直径、无数条半径
同一个圆中的直径都相等,半径都相等
圆的周长
C = πd 或 C = 2πr
能力提升
边
长
是
4
宽
2
长5
正方形内最大圆的直径长度等于正方形的边长。
长方形内最大圆的直径长度等于长方形的宽。
THE END
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
