苏科版数学九年级上册 2.2 圆的对称性 同步练习 2022—2023学年(含解析)
文档属性
| 名称 | 苏科版数学九年级上册 2.2 圆的对称性 同步练习 2022—2023学年(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 13:55:14 | ||
图片预览



文档简介
2.2 圆的对称性(精选题)-苏科版数学九年级上册
一.选择题
1.如图,在⊙O中,直径AB=8,弦DE⊥AB于点C,若AD=DE,则BC的长为( )
A. B. C.1 D.2
2.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
4.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
5.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
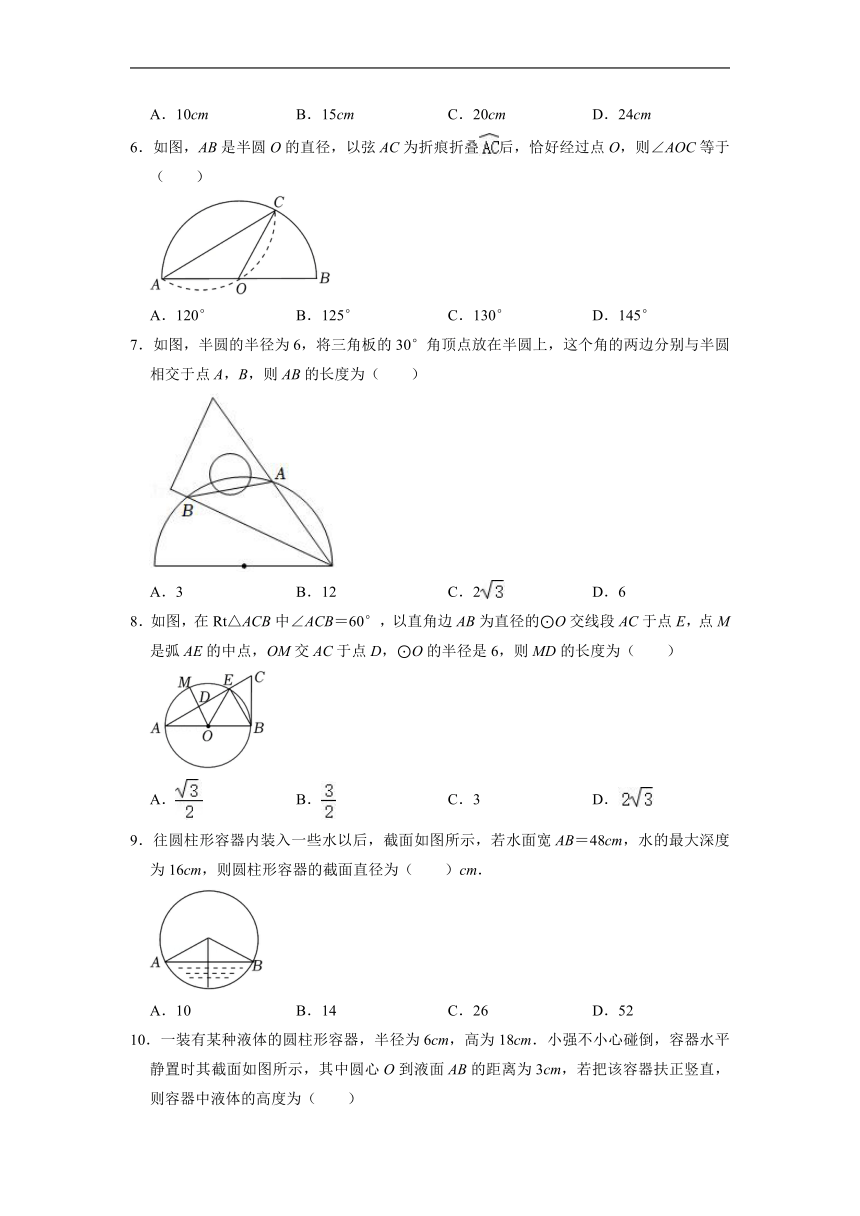
6.如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则∠AOC等于( )
A.120° B.125° C.130° D.145°
7.如图,半圆的半径为6,将三角板的30°角顶点放在半圆上,这个角的两边分别与半圆相交于点A,B,则AB的长度为( )
A.3 B.12 C.2 D.6
8.如图,在Rt△ACB中∠ACB=60°,以直角边AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,⊙O的半径是6,则MD的长度为( )
A. B. C.3 D.
9.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
10.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
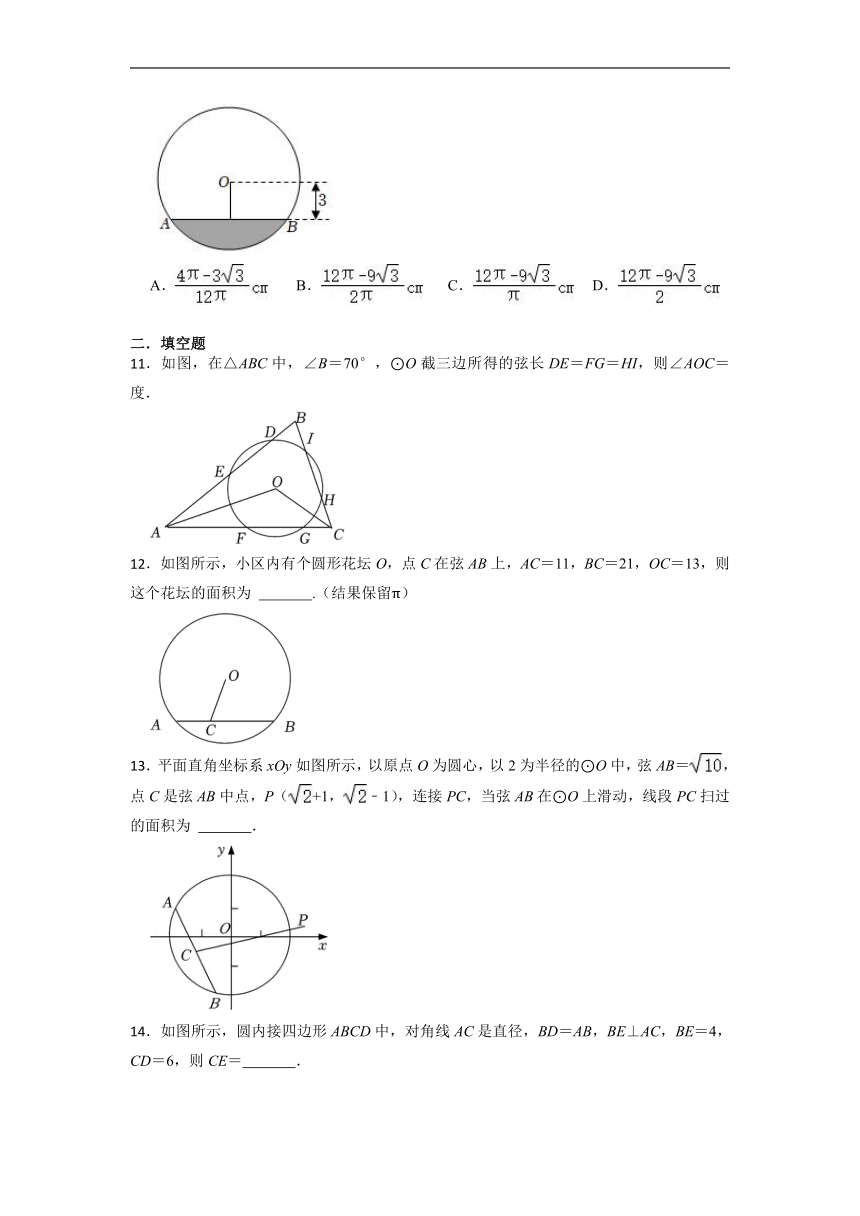
A. B. C. D.
二.填空题
.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 度.
.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
.平面直角坐标系xOy如图所示,以原点O为圆心,以2为半径的⊙O中,弦AB=,点C是弦AB中点,P(+1,﹣1),连接PC,当弦AB在⊙O上滑动,线段PC扫过的面积为 .
.如图所示,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,BE=4,CD=6,则CE= .
.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为 寸.
三.解答题
.如图,AB是⊙O的弦,OC交AB于点D,点D是弦AB(AB不是直径)的中点,若AB=8cm,CD=2cm,求⊙O的半径.
.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
.如图,已知C,D是以AB为直径的⊙O上的两点,连接BC,OC,OD,若OD∥BC,求证:D为的中点.
.如图,AB是⊙O直径,=,连接CD,过点D作射线CB的垂线,垂足为点G,交AB的延长线于点F.
(1)求证:AE=EF;
(2)若CD=EF=10,求BG的长.
.阅读以下材料,并按要求完成相应的任务关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使,连接BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形.(保留作图痕迹,标明字母,不写作法).
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连接PA,PD,PQ,QD.
……
参考答案与试题解析
一.选择题
1.【解答】解:∵DE⊥AB,AB过圆心O,
∴DC=CE=DE,∠ACD=∠BCD=90°,
∵AD=DE,
∴DC=AD,
∴∠DAC=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD=AB==4,
∵∠ADB=90°,∠DAB=30°,
∴∠ABD=60°,
∵∠DCB=90°,
∴∠CDB=30°,
∴BC=BD=,
故选:D.
2.【解答】解:如图,过点O作OC⊥AB于点C,连接OB,
则OB=7,
∵PA=4,PB=6,
∴AB=PA+PB=10,
∵OC⊥AB,
∴AC=BC=5,
∴PC=PB﹣BC=1,
在Rt△OBC中,根据勾股定理得:
OC2=OB2﹣BC2=72﹣52=24,
在Rt△OPC中,根据勾股定理得:
OP===5,
故选:D.
3.【解答】解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
4.【解答】解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
5.【解答】解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
6.【解答】解:O关于直线AC的对称点是Q,连接OQ,交AC于M,
则AC垂直平分OQ,
即AQ=AO,OM⊥AC,
∵OQ=OA,
∴OQ=AQ=OA,
∴△AQO是等边三角形,
∴∠AOQ=60°,
∵OQ⊥AC,OA=OC,
∴∠COQ=∠AOQ=60°,
∴∠AOC=60°+60°=120°,
故选:A.
7.【解答】解:连接OA,OB,
由圆周角定理得:∠AOB=2∠ACB,
∵∠ACB=30°,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=OB,
∵⊙O的半径为6,
∴AB=OA=6,
故选:D.
8.【解答】解:∵∠ABC=90°,∠ACB=60°,
∴∠A=30°,
∵M为弧AE的中点,OM过圆心O,
∴OM⊥AD,
∴∠ADO=90°,
∴OD=OA==3,
∴MD=OM﹣OD=6﹣3=3,
故选:C.
9.【解答】解:如图所示:
由题意得,OC⊥AB于D,DC=16cm,
∵AB=48cm,
∴BD=AB=×48=24(cm),
设半径为rcm,则OD=(r﹣16)cm,
在Rt△OBD中,
r2=242+(r﹣16)2,解得r=26,
所以2r=52,
故选:D.
10.【解答】解:连接OA,OB,如图,
根据题意得:OA=6cm,弦心距OC=3cm,
∴cos∠AOC=,
∴∠AOC=60°,则∠AOB=120°,
∴AC=3cm,AB=2AC=6cm,
∴S阴影=S扇形OAB﹣S△OAB=.
设把该容器扶正竖直后容器中液体的高度为h,
依题意得:,
∴,
故选:B.
二.填空题
.【解答】解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE=FG=HI,
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC=BAC,∠OCA=BCA,
∵∠B=70°,
∴∠BAC+∠BCA=180°﹣∠B=110°,
∴∠OAC+∠OCA
=(∠BAC+∠ACB)
=×110°
=55°,
∴∠AOC=180°﹣(∠OAC+∠OCA)
=180°﹣55°
=125°,
故答案为:125.
.【解答】解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
故答案为:400π.
.【解答】解:连接OC,OA,如图,
∵点C是弦AB中点,
∴OC⊥AB,AC=BC=AB=,
∴OC==.
∵弦AB在⊙O上滑动,
∴点C的轨迹为以点O为圆心,以为半径的圆,如图中的虚线⊙O,
过点P作该圆的切线PD,PE,连接OD,OE,PO,如上图,
则OD=OE=.
利用勾股定理可求得PO=,
∵PD,PE是虚线⊙O的切线,
∴OD⊥PD,OE⊥PE,PD=PE,∠DPO=∠EPO.
∵sin∠OPD==,
∴∠OPD=30°,
∴∠OPE=30°,
∴∠DOP=60°,∠EOP=60°,
∴∠DOE=120°.
∵线段PC扫过的面积为四边形DOEP的面积+大扇形ODE的面积,
∴线段PC扫过的面积为2×PD OD+
=+π.
故答案为:+π.
.【解答】解:延长BO交AD于点G,连接OD,如图所示:
∵OA=OD,AB=BD,
∴直线BG是线段AD的垂直平分线,
∴∠AGO=90°,AG=DG,
∵BE⊥AC,
∴∠BEO=∠AGO=90°,
在△AGO和△BEO中,
,
∴△AGO≌△BEO(AAS),
∴AG=BE,
∵BE=4,
∴AG=4,
∴DG=AG=4,
即AD=8,
∵AC是⊙O的直径,
∴∠ABC=∠ADC=90°,
∵CD=6,
∴AC=,
∵∠ABC=∠AEB=∠BEC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBE=90°,
∴∠BAE=∠CBE,
∴△ABE∽△BCE,
∴,
∴,
解得:CE=2或8,
当CE=8时,OE=OC﹣CE=5﹣8=﹣3,不符合题意.
故答案为:2.
.【解答】解:连接OC,
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE=CD=5寸,
设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+CE2=OC2,
即(x﹣1)2+52=x2,
解得x=13,
∴AB=26寸,
即直径AB的长为26寸,
故答案为:26.
三.解答题
.【解答】解:连接OA,设⊙O的半径为Rcm,则OA=OC=Rcm,
∵点D是弦AB(AB不是直径)的中点,OC过圆心O,AB=8cm,
∴AD=BD=4cm,OC⊥AB,
∴∠ODA=90°,
由勾股定理得:OD2+AD2=OA2,
(R﹣2)2+42=R2,
解得:R=5,
即⊙O的半径为5cm.
.【解答】(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
.【解答】证明:∵OB=OC,
∴∠B=∠C,
∵OD∥BC,
∴∠AOD=∠B,∠COD=∠C,
∴∠AOD=∠COD,
∴=,
即D为的中点.
.【解答】解:(1)连接AD,
∵AB是⊙O的直径,CD⊥AB,
∴∠CEB=90°,
∴∠C+∠CBE=90°,
又∵BG⊥DF,
∴∠F+∠FBG=90°,
∵∠CBE=∠FBG,
∴∠F=∠C=∠A,
∴DA=DF,
∵CD⊥AB,
∴AE=EF;
(2)∵AB是⊙O的直径,CD⊥AB,
∴CE=DE==5,
∵tan∠F===tan∠C=,
∴BE==,
∴BF=EF﹣BE=10﹣=,
在Rt△BFG中,tan∠F=,
设BG=x,则FG=2x,由勾股定理得,
BG2+FG2=BF2,
即x2+(2x)2=()2,
解得x=(x>0),
即BG=.
.【解答】解:(1)补全图形如解图所示:
(2)如图,
∵=,
∴PA=PQ,
∵PN⊥AB于点N,
∴∠PNA=∠PND=90°,
又∵AN=ND,PN=PN,
∴△APN≌△DPN(SAS),
∴∠PAD=∠PDA,PA=PD.
∴PD=PQ,
∴∠PQD=∠PDQ,
∵四边形APQB是圆内接四边形,
∴∠PAD+∠PQB=180°,
∴∠PDA+∠PQB=180°,
又∵∠PDA+∠PDB=180°,
∴∠PQB=∠PDB
∵∠BQD=∠BDQ,
∴BQ=BD.
一.选择题
1.如图,在⊙O中,直径AB=8,弦DE⊥AB于点C,若AD=DE,则BC的长为( )
A. B. C.1 D.2
2.已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=( )
A. B.4 C. D.5
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,若BE=CD=8,则⊙O的半径的长是( )
A.5 B.4 C.3 D.2
4.如图,在⊙O中,弦AB=5,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为( )
A.5 B.2.5 C.3 D.2
5.工人师傅为检测该厂生产的一种铁球的大小是否符合要求,设计了一个如图(1)所示的工件槽,其两个底角均为90°,将形状规则的铁球放入槽内时,若同时具有图(1)所示的A、B、E三个接触点,该球的大小就符合要求.图(2)是过球心及A、B、E三点的截面示意图,已知⊙O的直径就是铁球的直径,AB是⊙O的弦,CD切⊙O于点E,AC⊥CD、BD⊥CD,若CD=16cm,AC=BD=4cm,则这种铁球的直径为( )
A.10cm B.15cm C.20cm D.24cm
6.如图,AB是半圆O的直径,以弦AC为折痕折叠后,恰好经过点O,则∠AOC等于( )
A.120° B.125° C.130° D.145°
7.如图,半圆的半径为6,将三角板的30°角顶点放在半圆上,这个角的两边分别与半圆相交于点A,B,则AB的长度为( )
A.3 B.12 C.2 D.6
8.如图,在Rt△ACB中∠ACB=60°,以直角边AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,⊙O的半径是6,则MD的长度为( )
A. B. C.3 D.
9.往圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,水的最大深度为16cm,则圆柱形容器的截面直径为( )cm.
A.10 B.14 C.26 D.52
10.一装有某种液体的圆柱形容器,半径为6cm,高为18cm.小强不小心碰倒,容器水平静置时其截面如图所示,其中圆心O到液面AB的距离为3cm,若把该容器扶正竖直,则容器中液体的高度为( )
A. B. C. D.
二.填空题
.如图,在△ABC中,∠B=70°,⊙O截三边所得的弦长DE=FG=HI,则∠AOC= 度.
.如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 .(结果保留π)
.平面直角坐标系xOy如图所示,以原点O为圆心,以2为半径的⊙O中,弦AB=,点C是弦AB中点,P(+1,﹣1),连接PC,当弦AB在⊙O上滑动,线段PC扫过的面积为 .
.如图所示,圆内接四边形ABCD中,对角线AC是直径,BD=AB,BE⊥AC,BE=4,CD=6,则CE= .
.《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.其中卷九中记载了一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其意思是:如图,AB为⊙O的直径,弦CD⊥AB于点E,BE=1寸,CD=1尺,那么直径AB的长为多少寸?(注:1尺=10寸)根据题意,该圆的直径为 寸.
三.解答题
.如图,AB是⊙O的弦,OC交AB于点D,点D是弦AB(AB不是直径)的中点,若AB=8cm,CD=2cm,求⊙O的半径.
.如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E.
(1)求证:四边形ADOE是正方形;
(2)若AC=2cm,求⊙O的半径.
.如图,已知C,D是以AB为直径的⊙O上的两点,连接BC,OC,OD,若OD∥BC,求证:D为的中点.
.如图,AB是⊙O直径,=,连接CD,过点D作射线CB的垂线,垂足为点G,交AB的延长线于点F.
(1)求证:AE=EF;
(2)若CD=EF=10,求BG的长.
.阅读以下材料,并按要求完成相应的任务关于圆的任务.
关于圆的引理
在《阿基米德全集》的《引理集》中,记述了古希腊的数学家、物理学家阿基米德提出的六个关于圆的引理,其中第二个引理为:如图,在半圆O中,P是上的任意一点,PN⊥直径AB于点N,D在直径AB上,且AN=ND,在上取一点Q,使,连接BQ,则BQ=BD.
任务:
(1)尺规作图:请根据材料,在图中补全图形.(保留作图痕迹,标明字母,不写作法).
(2)善思小组的同学尝试证明该引理,请按照下面的证明思路,写出该证明的剩余部分.
证明:连接PA,PD,PQ,QD.
……
参考答案与试题解析
一.选择题
1.【解答】解:∵DE⊥AB,AB过圆心O,
∴DC=CE=DE,∠ACD=∠BCD=90°,
∵AD=DE,
∴DC=AD,
∴∠DAC=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BD=AB==4,
∵∠ADB=90°,∠DAB=30°,
∴∠ABD=60°,
∵∠DCB=90°,
∴∠CDB=30°,
∴BC=BD=,
故选:D.
2.【解答】解:如图,过点O作OC⊥AB于点C,连接OB,
则OB=7,
∵PA=4,PB=6,
∴AB=PA+PB=10,
∵OC⊥AB,
∴AC=BC=5,
∴PC=PB﹣BC=1,
在Rt△OBC中,根据勾股定理得:
OC2=OB2﹣BC2=72﹣52=24,
在Rt△OPC中,根据勾股定理得:
OP===5,
故选:D.
3.【解答】解:连接OC,
设⊙O的半径为R,则OE=8﹣R,
∵CD⊥AB,AB过圆心O,CD=8,
∴∠OEC=90°,CE=DE=4,
由勾股定理得:OC2=CE2+OE2,
R2=42+(8﹣R)2,
解得:R=5,
即⊙O的半径长是5,
故选:A.
4.【解答】解:连接OD,如图,
∵CD⊥OC,
∴∠DCO=90°,
∴CD=,
当OC的值最小时,CD的值最大,
而OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=×5=2.5,
即CD的最大值为2.5,
故选:B.
5.【解答】解:如图,连接OE,交AB于点F,连接OA,
∵AC⊥CD、BD⊥CD,
∴AC∥BD,
∵AC=BD=4cm,
∴四边形ACDB是平行四边形,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵CD切⊙O于点E,
∴OE⊥CD,
∴OE⊥AB,
∴四边形EFBD是矩形,AF=AB=×16=8(cm),
∴EF=BD=4cm,
设⊙O的半径为rcm,则OA=rcm,OF=OE﹣EF=(r﹣4)cm,
在Rt△AOF中,OA2=AF2+OF2,
∴r2=82+(r﹣4)2,
解得:r=10,
∴这种铁球的直径为20cm,
故选:C.
6.【解答】解:O关于直线AC的对称点是Q,连接OQ,交AC于M,
则AC垂直平分OQ,
即AQ=AO,OM⊥AC,
∵OQ=OA,
∴OQ=AQ=OA,
∴△AQO是等边三角形,
∴∠AOQ=60°,
∵OQ⊥AC,OA=OC,
∴∠COQ=∠AOQ=60°,
∴∠AOC=60°+60°=120°,
故选:A.
7.【解答】解:连接OA,OB,
由圆周角定理得:∠AOB=2∠ACB,
∵∠ACB=30°,
∴∠AOB=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=OB,
∵⊙O的半径为6,
∴AB=OA=6,
故选:D.
8.【解答】解:∵∠ABC=90°,∠ACB=60°,
∴∠A=30°,
∵M为弧AE的中点,OM过圆心O,
∴OM⊥AD,
∴∠ADO=90°,
∴OD=OA==3,
∴MD=OM﹣OD=6﹣3=3,
故选:C.
9.【解答】解:如图所示:
由题意得,OC⊥AB于D,DC=16cm,
∵AB=48cm,
∴BD=AB=×48=24(cm),
设半径为rcm,则OD=(r﹣16)cm,
在Rt△OBD中,
r2=242+(r﹣16)2,解得r=26,
所以2r=52,
故选:D.
10.【解答】解:连接OA,OB,如图,
根据题意得:OA=6cm,弦心距OC=3cm,
∴cos∠AOC=,
∴∠AOC=60°,则∠AOB=120°,
∴AC=3cm,AB=2AC=6cm,
∴S阴影=S扇形OAB﹣S△OAB=.
设把该容器扶正竖直后容器中液体的高度为h,
依题意得:,
∴,
故选:B.
二.填空题
.【解答】解:过点O作OM⊥DE于M,OK⊥FG于K,OP⊥HI于P,如图,
∵DE=FG=HI,
∴OM=OK=OP,
∴OA平分∠BAC,OC平分∠ACB,
∴∠OAC=BAC,∠OCA=BCA,
∵∠B=70°,
∴∠BAC+∠BCA=180°﹣∠B=110°,
∴∠OAC+∠OCA
=(∠BAC+∠ACB)
=×110°
=55°,
∴∠AOC=180°﹣(∠OAC+∠OCA)
=180°﹣55°
=125°,
故答案为:125.
.【解答】解:如图,连接OB,过点O作OD⊥AB于D,
∵OD⊥AB,OD过圆心,AB是弦,
∴AD=BD=AB=(AC+BC)=×(11+21)=16,
∴CD=BC﹣BD=21﹣16=5,
在Rt△COD中,OD2=OC2﹣CD2=132﹣52=144,
在Rt△BOD中,OB2=OD2+BD2=144+256=400,
∴S⊙O=π×OB2=400π,
故答案为:400π.
.【解答】解:连接OC,OA,如图,
∵点C是弦AB中点,
∴OC⊥AB,AC=BC=AB=,
∴OC==.
∵弦AB在⊙O上滑动,
∴点C的轨迹为以点O为圆心,以为半径的圆,如图中的虚线⊙O,
过点P作该圆的切线PD,PE,连接OD,OE,PO,如上图,
则OD=OE=.
利用勾股定理可求得PO=,
∵PD,PE是虚线⊙O的切线,
∴OD⊥PD,OE⊥PE,PD=PE,∠DPO=∠EPO.
∵sin∠OPD==,
∴∠OPD=30°,
∴∠OPE=30°,
∴∠DOP=60°,∠EOP=60°,
∴∠DOE=120°.
∵线段PC扫过的面积为四边形DOEP的面积+大扇形ODE的面积,
∴线段PC扫过的面积为2×PD OD+
=+π.
故答案为:+π.
.【解答】解:延长BO交AD于点G,连接OD,如图所示:
∵OA=OD,AB=BD,
∴直线BG是线段AD的垂直平分线,
∴∠AGO=90°,AG=DG,
∵BE⊥AC,
∴∠BEO=∠AGO=90°,
在△AGO和△BEO中,
,
∴△AGO≌△BEO(AAS),
∴AG=BE,
∵BE=4,
∴AG=4,
∴DG=AG=4,
即AD=8,
∵AC是⊙O的直径,
∴∠ABC=∠ADC=90°,
∵CD=6,
∴AC=,
∵∠ABC=∠AEB=∠BEC=90°,
∴∠BAE+∠ABE=90°,∠ABE+∠CBE=90°,
∴∠BAE=∠CBE,
∴△ABE∽△BCE,
∴,
∴,
解得:CE=2或8,
当CE=8时,OE=OC﹣CE=5﹣8=﹣3,不符合题意.
故答案为:2.
.【解答】解:连接OC,
∵弦CD⊥AB,AB为圆O的直径,
∴E为CD的中点,
又∵CD=10寸,
∴CE=DE=CD=5寸,
设OC=OA=x寸,则AB=2x寸,OE=(x﹣1)寸,
由勾股定理得:OE2+CE2=OC2,
即(x﹣1)2+52=x2,
解得x=13,
∴AB=26寸,
即直径AB的长为26寸,
故答案为:26.
三.解答题
.【解答】解:连接OA,设⊙O的半径为Rcm,则OA=OC=Rcm,
∵点D是弦AB(AB不是直径)的中点,OC过圆心O,AB=8cm,
∴AD=BD=4cm,OC⊥AB,
∴∠ODA=90°,
由勾股定理得:OD2+AD2=OA2,
(R﹣2)2+42=R2,
解得:R=5,
即⊙O的半径为5cm.
.【解答】(1)证明:∵OD⊥AB,OE⊥AC,
∴AD=AB,AE=AC,
∵AB=AC,
∴AD=AE,
∵∠ADO=∠A=∠AEO=90°,
∴四边形ADOE是正方形;
(2)解:连接OA,
∵AC=2cm,
∴AE=1cm,
在Rt△AOE中,OA==(cm),
答:⊙O的半径是cm.
.【解答】证明:∵OB=OC,
∴∠B=∠C,
∵OD∥BC,
∴∠AOD=∠B,∠COD=∠C,
∴∠AOD=∠COD,
∴=,
即D为的中点.
.【解答】解:(1)连接AD,
∵AB是⊙O的直径,CD⊥AB,
∴∠CEB=90°,
∴∠C+∠CBE=90°,
又∵BG⊥DF,
∴∠F+∠FBG=90°,
∵∠CBE=∠FBG,
∴∠F=∠C=∠A,
∴DA=DF,
∵CD⊥AB,
∴AE=EF;
(2)∵AB是⊙O的直径,CD⊥AB,
∴CE=DE==5,
∵tan∠F===tan∠C=,
∴BE==,
∴BF=EF﹣BE=10﹣=,
在Rt△BFG中,tan∠F=,
设BG=x,则FG=2x,由勾股定理得,
BG2+FG2=BF2,
即x2+(2x)2=()2,
解得x=(x>0),
即BG=.
.【解答】解:(1)补全图形如解图所示:
(2)如图,
∵=,
∴PA=PQ,
∵PN⊥AB于点N,
∴∠PNA=∠PND=90°,
又∵AN=ND,PN=PN,
∴△APN≌△DPN(SAS),
∴∠PAD=∠PDA,PA=PD.
∴PD=PQ,
∴∠PQD=∠PDQ,
∵四边形APQB是圆内接四边形,
∴∠PAD+∠PQB=180°,
∴∠PDA+∠PQB=180°,
又∵∠PDA+∠PDB=180°,
∴∠PQB=∠PDB
∵∠BQD=∠BDQ,
∴BQ=BD.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
