人教版数学 九年级上册 第24章圆—— 隐圆练习 2022—2023学年(含解析)
文档属性
| 名称 | 人教版数学 九年级上册 第24章圆—— 隐圆练习 2022—2023学年(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 532.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 13:56:07 | ||
图片预览


文档简介
第24章——隐圆
一、选择
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
2.如右图,在矩形ABCD中,AB=10,AD=12,P为矩形内一点,∠APB=90°,连接PD,则PD的最小值为( )
A.8 B.2 C.10 D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段PB的最小值为( )
A. B.1 C.2 D.3
4.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为线段AB上的动点,连接CD,过点B作BE⊥CD交CD于点E,则在点D的运动过程中,求线段AE的最小值为( )
A.10 B.3 C.5 D.
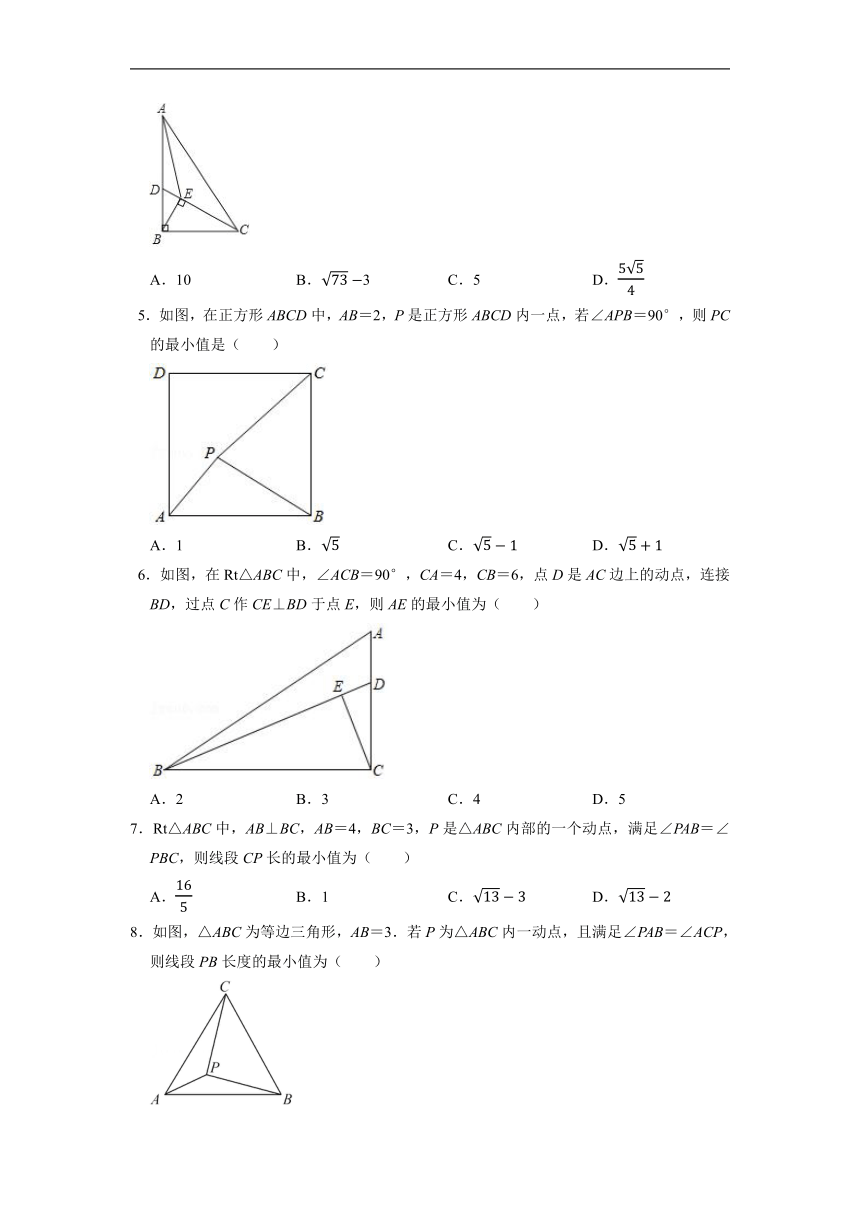
5.如图,在正方形ABCD中,AB=2,P是正方形ABCD内一点,若∠APB=90°,则PC的最小值是( )
A.1 B. C. D.
6.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,则AE的最小值为( )
A.2 B.3 C.4 D.5
7.Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.1 C. D.
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
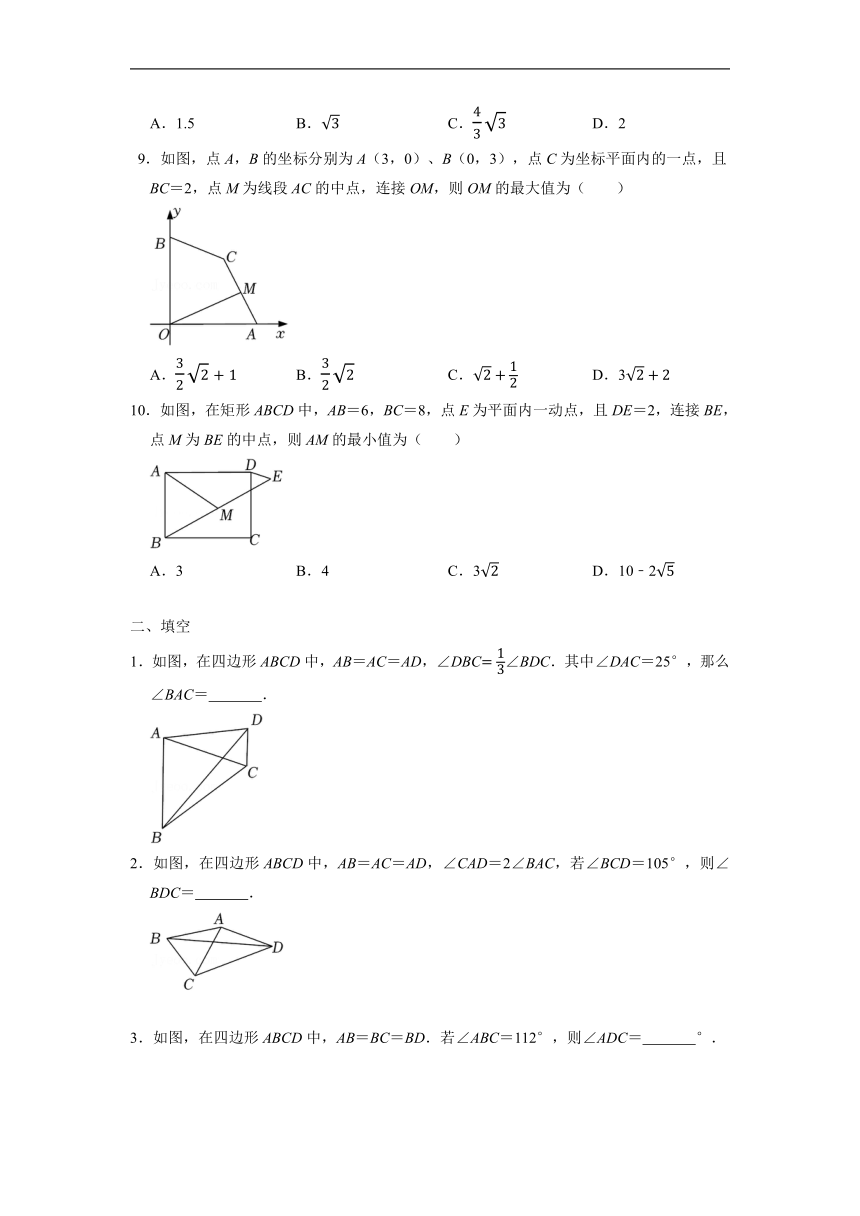
9.如图,点A,B的坐标分别为A(3,0)、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.3
10.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,则AM的最小值为( )
A.3 B.4 C.3 D.10﹣2
二、填空
1.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= .
2.如图,在四边形ABCD中,AB=AC=AD,∠CAD=2∠BAC,若∠BCD=105°,则∠BDC= .
3.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= °.
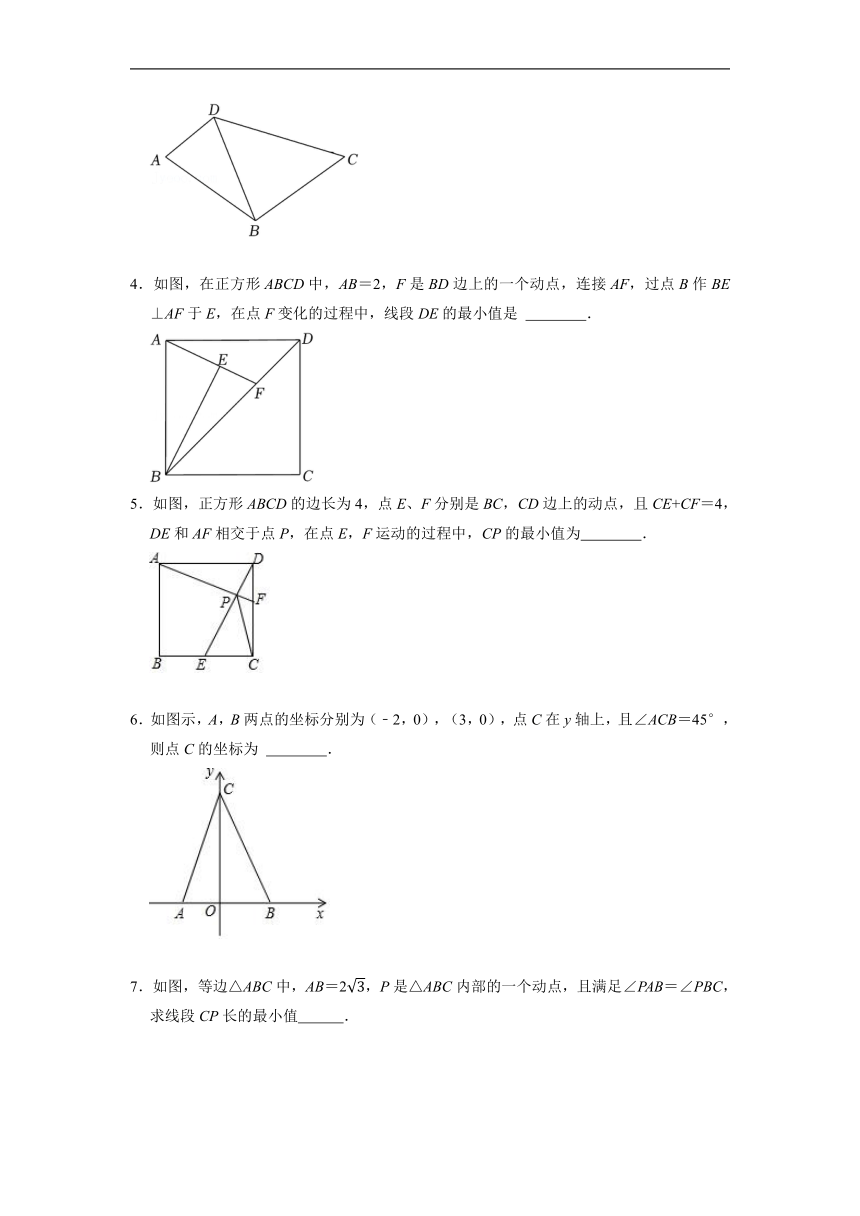
4.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是 .
5.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为 .
6.如图示,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴上,且∠ACB=45°,则点C的坐标为 .
7.如图,等边△ABC中,AB=2,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值 .
8.如图,△ABC中,AB=AC=2,BC=2,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是 .
9.如图,正方形ABCD的边长为4,点E是正方形外一动点,且点E在CD的右侧,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为 .
10.如图,点D为边长是4的等边△ABC边AB左侧一动点,不与点A,B重合的动点D在运动过程中始终保持∠ADB=120°不变,则四边形ADBC的面积S的最大值是 .
11.在等边三角形ABC中,D,E分别是AC,BC上的点,AE与BD相交于点P.若△BCD的面积是12,BE=6,∠APB=120°,则△ABP的外接圆的半径长为 .
12.如图,四边形ABCD中,AB=AD=6,BD=4,∠BCD=30°,我们知道满足条件的点C不是唯一的,则AC长的最大值为 .
13.如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为 .
第24章——隐圆(答案)
一、选择
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
【解答】解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
2.如右图,在矩形ABCD中,AB=10,AD=12,P为矩形内一点,∠APB=90°,连接PD,则PD的最小值为( )
A.8 B.2 C.10 D.
【解答】解:如图,以AB为直径作⊙O,连接OD在矩形ABCD内部交⊙O于点P,则此时PD有最小值.
矩形ABCD中,AB=10,AD=12,
∴OP=AO=5,∠BAD=90°,
∴OD,
∴PD=OD﹣OP=13﹣5=8,
即PD的最小值为8.
故选:A.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段PB的最小值为( )
A. B.1 C.2 D.3
【解答】解:∵∠ACB=90°,
∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB,
∴∠CAP+∠ACP=90°,
∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB,
∴PB=OB﹣OP2.
∴PC最小值为2.
故选:C.
4.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为线段AB上的动点,连接CD,过点B作BE⊥CD交CD于点E,则在点D的运动过程中,求线段AE的最小值为( )
A.10 B.3 C.5 D.
【解答】解:设BC的中点为点O,以O为圆心,BC为直径画圆,如图:
∵BE⊥CD,BC=6,
∴点E在以O为圆心,半径为BC=3的圆上,
∵点E在半径为3的⊙O上,
∴OE=OB=3,
∵∠ABC=90°,AB=8,
∴AO,
∵两点之间线段最短,
∴当A、O、E三点共线时,AE取得最小值,
此时,AE=AO﹣OE3,
故选:B.
5.如图,在正方形ABCD中,AB=2,P是正方形ABCD内一点,若∠APB=90°,则PC的最小值是( )
A.1 B. C. D.
【解答】解:如图所示:取AB的中点O,以O为圆心,OA为半径作⊙O.
∵∠APB=90°,
∴点P在⊙O上.
∵AB=2,
∴OP=1,AB=1.
当O、P、C在一条直线上时,PC有最小值.
PC的最小值=OC﹣OPOP1,
故选:C.
6.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,则AE的最小值为( )
A.2 B.3 C.4 D.5
【解答】解:如图,取BC中点F,连接AE、EF.
∵CE⊥BD,∠BEC=90°,
∴点E在以BC长为直径的圆周上上运动,当点A、E、F在同一直线上时,AE最短.
∵CA=4,CB=6,
∴BFBC=3,
∴AF5,
∴AE=AF﹣BF=5﹣3=2,
即AE的最小值为2.
故选:A.
7.Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.1 C. D.
【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∠OBC=90°,BC=3,OB=2,
∴OC,
∴CP=OC﹣OP2.
∴CP最小值为2.
故选:D.
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
【解答】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CDAC,∠PAC=∠ACP=30°,∠ABD∠ABC=30°,
∴PD,BD,
∴PB=BD﹣PD.
故选:B.
9.如图,点A,B的坐标分别为A(3,0)、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.3
【解答】解:如图,作点A关于点O的对称点A'(﹣3,0),
则点O是AA'的中点,
又∵点M是AC的中点,
∴OM是△AA'C的中位线,
∴OM,
∴当A'C最大时,OM最大,
∵点C为坐标平面内的一点,且BC=2,
∴点C在以B为圆心,2为半径的⊙B上运动,
∴当A'C经过圆心B时,A′C最大,即点C在图中C'位置.
A'C'=AB+BC'=3.
∴OM的最大值.
故选:A.
10.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,则AM的最小值为( )
A.3 B.4 C.3 D.10﹣2
【解答】解:由题意知:E点在以D为圆心,以2为半径的圆上,连接BD,取BD的中点O,连接AO,MO,
在矩形ABCD中,∠BAD=90°,AB=8,BC=6,
∴BD,
∵O为BD的中点,
∴AOBD=5,
∵M为BE的中点,DE=2,
∴OMDE=1,
∵AM>AO﹣OM,即AM>4,
∴当A,O,M三点共线时,AM有最小值为4,
故选:B.
二、填空
1.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= 75° .
【解答】解:如图:
∵AB=AC=AD,
∴B、C、D在以A为圆心,以AB为半径的同一个圆上,
∵∠DAC=25°,
∴∠DBC∠DAC=12.5°,
∵∠DBC∠BDC,
∴∠BDC=3∠DBC=37.5°,
∴∠BAC=2∠BDC=75°,
故答案为:75°.
2.如图,在四边形ABCD中,AB=AC=AD,∠CAD=2∠BAC,若∠BCD=105°,则∠BDC= 25° .
【解答】解:以A为圆心,AB为半径画圆,
∴∠CAD=2∠CBD,∠BAC=2∠BDC,
∵∠CAD=2∠BAC,
∴∠CBD=2∠BDC,
∵∠CBD+∠BDC+∠BCD=180°,
∴3∠CBD+105°=180°,
∴∠CBD=25°.
故答案为:25°.
3.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= 124 °.
【解答】解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠EABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
故答案为:124.
4.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是 1 .
【解答】解:如图,∵BE⊥AF于E,
∴E在以AB为直径圆心为O的圆上,
∴当O、E、D三点共线的时候线段DE最小,
∵AB=2,四边形ABCD为正方形,
∴AO=1=OE,AD=2,
∴OD,
∴段DE最小值为OD﹣OF1.
故答案为:1.
5.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为 22 .
【解答】解:在正方形ABCD中,AD=CD=BC=4,∠ADC=∠BCD=90°,
∵CE+CF=4,CF+DF=4,
∴CE=DF,
在△ADF和△DCE中,,
∴△ADF≌△DCE(SAS),
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠DAP+∠FDP=90°,
∴∠APD=90°,
∴点P在以AD为直径的圆上,
设AD的中点为G,
由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:
∵CD=4,DG=2,
∴CG2,
∴CP=CG﹣PG=22,
故答案为:22.
6.如图示,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴上,且∠ACB=45°,则点C的坐标为 (0,6)或(0,﹣6) .
【解答】解:在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于C,连接CB,CA.
∵∠ACB∠AFB=45°,
∵B(﹣2,0),A(3,0),△ABF是等腰直角三角形,
∴F(,),FA=FB=FC,设C(0.m),
则()2+(m)2=()2,
解得m=6或﹣1(舍弃)
∴C(0,6),
根据对称性可知C′(0,﹣6)也符合条件,
综上所述,点C的坐标为(0,6)或(0,﹣6).
故答案为(0,6)或(0,﹣6).
7.如图,等边△ABC中,AB=2,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值 2 .
【解答】解:以AB为边向左作等边三角形ABD,作△ABD使得外接圆⊙O.连接OC,OP.
∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠PAB=∠PBC,
∴∠PAB+∠PBA=∠PBC+∠PBA=∠ABC=60°,
∴∠APB=120°,
∵△ADB是等边三角形,
∴∠D=60°,
∴∠D+∠APB=180°,
∴点P在⊙O上,
∵AB=2,O外心,
∴OA=OB=2,OB平分∠ABD,
∴∠ABO=30°,
∴∠OBC=90°,
∴OC4,
∴PC≥OC﹣OP,
∴PC≥2,
∴PC的最小值为2,
故答案为2.
8.如图,△ABC中,AB=AC=2,BC=2,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是 .
【解答】解:如图,作AH⊥BC于H,
∵AB=AC=2,BC=2,
∴BHBC,
∴AH1,
∴sin∠ABC,
∴∠ABC=∠ACB=30°,∠BAC=120°,
以A为圆心,AB为半径作⊙A,延长HA交⊙A于点D,
∵∠BDC=60°,
∴点D在⊙O上运动,当D运动到如图的位置时,△DBC面积的最大值,最大值为:.
故答案为:.
9.如图,正方形ABCD的边长为4,点E是正方形外一动点,且点E在CD的右侧,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为 2+2 .
【解答】解:如图,连接AC,BD交于点O,连接PO,EO,
∵∠AED=45°,∠ACD=45°,
∴A,C,E,D四点共圆,
∵正方形ABCD的边长为4,
∴OE=ODBD=2,
∵P为AB的中点,O是BD的中点,
∴OPAD=2,
∵PE≤OP+OE=2+2,
∴当点O在线段PE上时,PE=OP+OE=2+2,
即线段PE的最大值为2+2,
故答案为:2+2.
10.如图,点D为边长是4的等边△ABC边AB左侧一动点,不与点A,B重合的动点D在运动过程中始终保持∠ADB=120°不变,则四边形ADBC的面积S的最大值是 16 .
【解答】解:∵△ABC是等边三角形,
∴AB=AC=BC=4,∠ACB=∠ABC=∠BAC=60°,
∵∠ADB=120°,
∴∠ADB+∠ACB=180°,
∴四边形ACBD是圆内接四边形,
∴OA=OBAB4,
∴⊙O直径为8.
如图,作四边形ACBD的外接圆⊙O,将△ADC绕点C逆时针旋转60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线,
∵DC=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDHCD2,
∴当CD最大时,四边形ADBC的面积最大,
∴当CD为⊙O的直径时,CD的值最大,
即CD=8,
∴四边形ADBC的面积的最大值为 CD2=16,
故答案为:16.
11.在等边三角形ABC中,D,E分别是AC,BC上的点,AE与BD相交于点P.若△BCD的面积是12,BE=6,∠APB=120°,则△ABP的外接圆的半径长为 .
【解答】解:如图以AB为边向外作等边三角形ABK,作△ABK的外接圆⊙O,连接OA,OB,过点O作OJ⊥AB于J,过点B作BH⊥AC于H.
∵△ABK是等边三角形,
∴∠K=60°,
∵∠APB=120°,
∴∠K+∠APB=180°,
∴A,K,B,P四点共圆,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠C=60°,
∵∠APB=120°,
∴∠PAB+∠ABP=∠PAB+∠CAE=60°,
∴∠CAE=∠ABD,
∴△BAD≌△ACE(ASA),
∴AD=EC,
∵AC=BC,
∴BE=CD=6,
∵S△BCD CD BH=12,
∴BH=4,
∴AB8,
∵OA=OB,OJ⊥AB,
∴AJ=JB=4,
∵∠OAB=30°,
∴OA,
∴△APB的外接圆的半径为.
故答案为.
12.如图,四边形ABCD中,AB=AD=6,BD=4,∠BCD=30°,我们知道满足条件的点C不是唯一的,则AC长的最大值为 424 .
【解答】解:如图,作△BCD的外接圆⊙O,连接OB,OD,OC,OA,设AO交BD于T.
∵∠BOD=2∠BCD=60°,OB=OD,
∴△OBD是等边三角形,
∴OB=OD=OC=BD=4,
∵AB=AD=6,
∴OA垂直平分线段BD,
∴BT=DT=2,
∴AT4,
OT2,
∴OA=AT+OT=42,
∵AC≤OA+OC,
∴AC≤424,
∴AC的最大值为424.
13.如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为 2 .
【解答】解:过B作BD∥AC交x轴于D,
∵C是OB的中点,
∴OA=AD,
∴ACBD,
∴当BD取最小值时,AC最小,
由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,
∵A(3,0),
∴D(6,0),
∵M(3,4),
∴DM5,
∴BD=5﹣1=4,
∴ACBD=2,即线段AC的最小值为2;
故答案为:2.
一、选择
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
2.如右图,在矩形ABCD中,AB=10,AD=12,P为矩形内一点,∠APB=90°,连接PD,则PD的最小值为( )
A.8 B.2 C.10 D.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段PB的最小值为( )
A. B.1 C.2 D.3
4.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为线段AB上的动点,连接CD,过点B作BE⊥CD交CD于点E,则在点D的运动过程中,求线段AE的最小值为( )
A.10 B.3 C.5 D.
5.如图,在正方形ABCD中,AB=2,P是正方形ABCD内一点,若∠APB=90°,则PC的最小值是( )
A.1 B. C. D.
6.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,则AE的最小值为( )
A.2 B.3 C.4 D.5
7.Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.1 C. D.
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
9.如图,点A,B的坐标分别为A(3,0)、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.3
10.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,则AM的最小值为( )
A.3 B.4 C.3 D.10﹣2
二、填空
1.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= .
2.如图,在四边形ABCD中,AB=AC=AD,∠CAD=2∠BAC,若∠BCD=105°,则∠BDC= .
3.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= °.
4.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是 .
5.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为 .
6.如图示,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴上,且∠ACB=45°,则点C的坐标为 .
7.如图,等边△ABC中,AB=2,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值 .
8.如图,△ABC中,AB=AC=2,BC=2,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是 .
9.如图,正方形ABCD的边长为4,点E是正方形外一动点,且点E在CD的右侧,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为 .
10.如图,点D为边长是4的等边△ABC边AB左侧一动点,不与点A,B重合的动点D在运动过程中始终保持∠ADB=120°不变,则四边形ADBC的面积S的最大值是 .
11.在等边三角形ABC中,D,E分别是AC,BC上的点,AE与BD相交于点P.若△BCD的面积是12,BE=6,∠APB=120°,则△ABP的外接圆的半径长为 .
12.如图,四边形ABCD中,AB=AD=6,BD=4,∠BCD=30°,我们知道满足条件的点C不是唯一的,则AC长的最大值为 .
13.如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为 .
第24章——隐圆(答案)
一、选择
1.如图,四边形ABCD中,连接AC、BD,点O为AB的中点,若∠ADB=∠ACB=90°,则下面结论不一定正确的是( )
A.DC=CB
B.∠DAC=∠DBC
C.∠BCD+∠BAD=180°
D.点A、C、D到点O的距离相等
【解答】解:∵点O为AB的中点,∠ADB=∠ACB=90°,
∴D,C在以O为圆心,AB为直径的圆上,如图,
∴∠DAC=∠DBC,∠BCD+∠BAD=180°,点A、C、D到点O的距离相等,
当∠DAC=∠BAC时,DC=CB,而题目中未给出.
故选:A.
2.如右图,在矩形ABCD中,AB=10,AD=12,P为矩形内一点,∠APB=90°,连接PD,则PD的最小值为( )
A.8 B.2 C.10 D.
【解答】解:如图,以AB为直径作⊙O,连接OD在矩形ABCD内部交⊙O于点P,则此时PD有最小值.
矩形ABCD中,AB=10,AD=12,
∴OP=AO=5,∠BAD=90°,
∴OD,
∴PD=OD﹣OP=13﹣5=8,
即PD的最小值为8.
故选:A.
3.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.P是△ABC内部的一个动点,且满足∠PAC=∠PCB,则线段PB的最小值为( )
A. B.1 C.2 D.3
【解答】解:∵∠ACB=90°,
∴∠ACP+∠PCB=90°,
∵∠PAC=∠PCB,
∴∠CAP+∠ACP=90°,
∴∠APC=90°,
∴点P在以AC为直径的⊙O上,连接OB交⊙O于点P,此时PB最小,
在Rt△CBO中,∠OCB=90°,BC=3,OC=2,
∴OB,
∴PB=OB﹣OP2.
∴PC最小值为2.
故选:C.
4.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,D为线段AB上的动点,连接CD,过点B作BE⊥CD交CD于点E,则在点D的运动过程中,求线段AE的最小值为( )
A.10 B.3 C.5 D.
【解答】解:设BC的中点为点O,以O为圆心,BC为直径画圆,如图:
∵BE⊥CD,BC=6,
∴点E在以O为圆心,半径为BC=3的圆上,
∵点E在半径为3的⊙O上,
∴OE=OB=3,
∵∠ABC=90°,AB=8,
∴AO,
∵两点之间线段最短,
∴当A、O、E三点共线时,AE取得最小值,
此时,AE=AO﹣OE3,
故选:B.
5.如图,在正方形ABCD中,AB=2,P是正方形ABCD内一点,若∠APB=90°,则PC的最小值是( )
A.1 B. C. D.
【解答】解:如图所示:取AB的中点O,以O为圆心,OA为半径作⊙O.
∵∠APB=90°,
∴点P在⊙O上.
∵AB=2,
∴OP=1,AB=1.
当O、P、C在一条直线上时,PC有最小值.
PC的最小值=OC﹣OPOP1,
故选:C.
6.如图,在Rt△ABC中,∠ACB=90°,CA=4,CB=6,点D是AC边上的动点,连接BD,过点C作CE⊥BD于点E,则AE的最小值为( )
A.2 B.3 C.4 D.5
【解答】解:如图,取BC中点F,连接AE、EF.
∵CE⊥BD,∠BEC=90°,
∴点E在以BC长为直径的圆周上上运动,当点A、E、F在同一直线上时,AE最短.
∵CA=4,CB=6,
∴BFBC=3,
∴AF5,
∴AE=AF﹣BF=5﹣3=2,
即AE的最小值为2.
故选:A.
7.Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.1 C. D.
【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∠OBC=90°,BC=3,OB=2,
∴OC,
∴CP=OC﹣OP2.
∴CP最小值为2.
故选:D.
8.如图,△ABC为等边三角形,AB=3.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为( )
A.1.5 B. C. D.2
【解答】解:∵△ABC是等边三角形,
∴∠ABC=∠BAC=60°,AC=AB=3,
∵∠PAB=∠ACP,
∴∠PAC+∠ACP=60°,
∴∠APC=120°,
∴点P的运动轨迹是,
设所在圆的圆心为O,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:
此时PA=PC,OB⊥AC,
则AD=CDAC,∠PAC=∠ACP=30°,∠ABD∠ABC=30°,
∴PD,BD,
∴PB=BD﹣PD.
故选:B.
9.如图,点A,B的坐标分别为A(3,0)、B(0,3),点C为坐标平面内的一点,且BC=2,点M为线段AC的中点,连接OM,则OM的最大值为( )
A. B. C. D.3
【解答】解:如图,作点A关于点O的对称点A'(﹣3,0),
则点O是AA'的中点,
又∵点M是AC的中点,
∴OM是△AA'C的中位线,
∴OM,
∴当A'C最大时,OM最大,
∵点C为坐标平面内的一点,且BC=2,
∴点C在以B为圆心,2为半径的⊙B上运动,
∴当A'C经过圆心B时,A′C最大,即点C在图中C'位置.
A'C'=AB+BC'=3.
∴OM的最大值.
故选:A.
10.如图,在矩形ABCD中,AB=6,BC=8,点E为平面内一动点,且DE=2,连接BE,点M为BE的中点,则AM的最小值为( )
A.3 B.4 C.3 D.10﹣2
【解答】解:由题意知:E点在以D为圆心,以2为半径的圆上,连接BD,取BD的中点O,连接AO,MO,
在矩形ABCD中,∠BAD=90°,AB=8,BC=6,
∴BD,
∵O为BD的中点,
∴AOBD=5,
∵M为BE的中点,DE=2,
∴OMDE=1,
∵AM>AO﹣OM,即AM>4,
∴当A,O,M三点共线时,AM有最小值为4,
故选:B.
二、填空
1.如图,在四边形ABCD中,AB=AC=AD,∠DBC∠BDC.其中∠DAC=25°,那么∠BAC= 75° .
【解答】解:如图:
∵AB=AC=AD,
∴B、C、D在以A为圆心,以AB为半径的同一个圆上,
∵∠DAC=25°,
∴∠DBC∠DAC=12.5°,
∵∠DBC∠BDC,
∴∠BDC=3∠DBC=37.5°,
∴∠BAC=2∠BDC=75°,
故答案为:75°.
2.如图,在四边形ABCD中,AB=AC=AD,∠CAD=2∠BAC,若∠BCD=105°,则∠BDC= 25° .
【解答】解:以A为圆心,AB为半径画圆,
∴∠CAD=2∠CBD,∠BAC=2∠BDC,
∵∠CAD=2∠BAC,
∴∠CBD=2∠BDC,
∵∠CBD+∠BDC+∠BCD=180°,
∴3∠CBD+105°=180°,
∴∠CBD=25°.
故答案为:25°.
3.如图,在四边形ABCD中,AB=BC=BD.若∠ABC=112°,则∠ADC= 124 °.
【解答】解:∵AB=BD=BC,
∴A、D、C在以B为圆心,以AB为半径的圆上,
如图,作圆周角∠AEC,
∵∠ABC=112°,
∴∠EABC=56°,
∵四边形ADCE是⊙B的圆内接四边形,
∴∠ADC+∠E=180°,
∴∠ADC=180°﹣56°=124°,
故答案为:124.
4.如图,在正方形ABCD中,AB=2,F是BD边上的一个动点,连接AF,过点B作BE⊥AF于E,在点F变化的过程中,线段DE的最小值是 1 .
【解答】解:如图,∵BE⊥AF于E,
∴E在以AB为直径圆心为O的圆上,
∴当O、E、D三点共线的时候线段DE最小,
∵AB=2,四边形ABCD为正方形,
∴AO=1=OE,AD=2,
∴OD,
∴段DE最小值为OD﹣OF1.
故答案为:1.
5.如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为 22 .
【解答】解:在正方形ABCD中,AD=CD=BC=4,∠ADC=∠BCD=90°,
∵CE+CF=4,CF+DF=4,
∴CE=DF,
在△ADF和△DCE中,,
∴△ADF≌△DCE(SAS),
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠DAP+∠FDP=90°,
∴∠APD=90°,
∴点P在以AD为直径的圆上,
设AD的中点为G,
由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:
∵CD=4,DG=2,
∴CG2,
∴CP=CG﹣PG=22,
故答案为:22.
6.如图示,A,B两点的坐标分别为(﹣2,0),(3,0),点C在y轴上,且∠ACB=45°,则点C的坐标为 (0,6)或(0,﹣6) .
【解答】解:在x轴的上方作等腰直角△ABF,FB=FA,∠BAF=90°,以F为圆心,FA为半径作⊙F交y轴于C,连接CB,CA.
∵∠ACB∠AFB=45°,
∵B(﹣2,0),A(3,0),△ABF是等腰直角三角形,
∴F(,),FA=FB=FC,设C(0.m),
则()2+(m)2=()2,
解得m=6或﹣1(舍弃)
∴C(0,6),
根据对称性可知C′(0,﹣6)也符合条件,
综上所述,点C的坐标为(0,6)或(0,﹣6).
故答案为(0,6)或(0,﹣6).
7.如图,等边△ABC中,AB=2,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,求线段CP长的最小值 2 .
【解答】解:以AB为边向左作等边三角形ABD,作△ABD使得外接圆⊙O.连接OC,OP.
∵△ABC是等边三角形,
∴∠ABC=60°,
∵∠PAB=∠PBC,
∴∠PAB+∠PBA=∠PBC+∠PBA=∠ABC=60°,
∴∠APB=120°,
∵△ADB是等边三角形,
∴∠D=60°,
∴∠D+∠APB=180°,
∴点P在⊙O上,
∵AB=2,O外心,
∴OA=OB=2,OB平分∠ABD,
∴∠ABO=30°,
∴∠OBC=90°,
∴OC4,
∴PC≥OC﹣OP,
∴PC≥2,
∴PC的最小值为2,
故答案为2.
8.如图,△ABC中,AB=AC=2,BC=2,D点是△ABC所在平面上的一个动点,且∠BDC=60°,则△DBC面积的最大值是 .
【解答】解:如图,作AH⊥BC于H,
∵AB=AC=2,BC=2,
∴BHBC,
∴AH1,
∴sin∠ABC,
∴∠ABC=∠ACB=30°,∠BAC=120°,
以A为圆心,AB为半径作⊙A,延长HA交⊙A于点D,
∵∠BDC=60°,
∴点D在⊙O上运动,当D运动到如图的位置时,△DBC面积的最大值,最大值为:.
故答案为:.
9.如图,正方形ABCD的边长为4,点E是正方形外一动点,且点E在CD的右侧,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为 2+2 .
【解答】解:如图,连接AC,BD交于点O,连接PO,EO,
∵∠AED=45°,∠ACD=45°,
∴A,C,E,D四点共圆,
∵正方形ABCD的边长为4,
∴OE=ODBD=2,
∵P为AB的中点,O是BD的中点,
∴OPAD=2,
∵PE≤OP+OE=2+2,
∴当点O在线段PE上时,PE=OP+OE=2+2,
即线段PE的最大值为2+2,
故答案为:2+2.
10.如图,点D为边长是4的等边△ABC边AB左侧一动点,不与点A,B重合的动点D在运动过程中始终保持∠ADB=120°不变,则四边形ADBC的面积S的最大值是 16 .
【解答】解:∵△ABC是等边三角形,
∴AB=AC=BC=4,∠ACB=∠ABC=∠BAC=60°,
∵∠ADB=120°,
∴∠ADB+∠ACB=180°,
∴四边形ACBD是圆内接四边形,
∴OA=OBAB4,
∴⊙O直径为8.
如图,作四边形ACBD的外接圆⊙O,将△ADC绕点C逆时针旋转60°,得到△BHC,
∴CD=CH,∠DAC=∠HBC,
∵四边形ACBD是圆内接四边形,
∴∠DAC+∠DBC=180°,
∴∠DBC+∠HBC=180°,
∴点D,点B,点H三点共线,
∵DC=CH,∠CDH=60°,
∴△DCH是等边三角形,
∵四边形ADBC的面积S=S△ADC+S△BDC=S△CDHCD2,
∴当CD最大时,四边形ADBC的面积最大,
∴当CD为⊙O的直径时,CD的值最大,
即CD=8,
∴四边形ADBC的面积的最大值为 CD2=16,
故答案为:16.
11.在等边三角形ABC中,D,E分别是AC,BC上的点,AE与BD相交于点P.若△BCD的面积是12,BE=6,∠APB=120°,则△ABP的外接圆的半径长为 .
【解答】解:如图以AB为边向外作等边三角形ABK,作△ABK的外接圆⊙O,连接OA,OB,过点O作OJ⊥AB于J,过点B作BH⊥AC于H.
∵△ABK是等边三角形,
∴∠K=60°,
∵∠APB=120°,
∴∠K+∠APB=180°,
∴A,K,B,P四点共圆,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠C=60°,
∵∠APB=120°,
∴∠PAB+∠ABP=∠PAB+∠CAE=60°,
∴∠CAE=∠ABD,
∴△BAD≌△ACE(ASA),
∴AD=EC,
∵AC=BC,
∴BE=CD=6,
∵S△BCD CD BH=12,
∴BH=4,
∴AB8,
∵OA=OB,OJ⊥AB,
∴AJ=JB=4,
∵∠OAB=30°,
∴OA,
∴△APB的外接圆的半径为.
故答案为.
12.如图,四边形ABCD中,AB=AD=6,BD=4,∠BCD=30°,我们知道满足条件的点C不是唯一的,则AC长的最大值为 424 .
【解答】解:如图,作△BCD的外接圆⊙O,连接OB,OD,OC,OA,设AO交BD于T.
∵∠BOD=2∠BCD=60°,OB=OD,
∴△OBD是等边三角形,
∴OB=OD=OC=BD=4,
∵AB=AD=6,
∴OA垂直平分线段BD,
∴BT=DT=2,
∴AT4,
OT2,
∴OA=AT+OT=42,
∵AC≤OA+OC,
∴AC≤424,
∴AC的最大值为424.
13.如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO的中点为C,则线段AC的最小值为 2 .
【解答】解:过B作BD∥AC交x轴于D,
∵C是OB的中点,
∴OA=AD,
∴ACBD,
∴当BD取最小值时,AC最小,
由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,
∵A(3,0),
∴D(6,0),
∵M(3,4),
∴DM5,
∴BD=5﹣1=4,
∴ACBD=2,即线段AC的最小值为2;
故答案为:2.
同课章节目录
