用坐标表示平移[下学期]
图片预览





文档简介
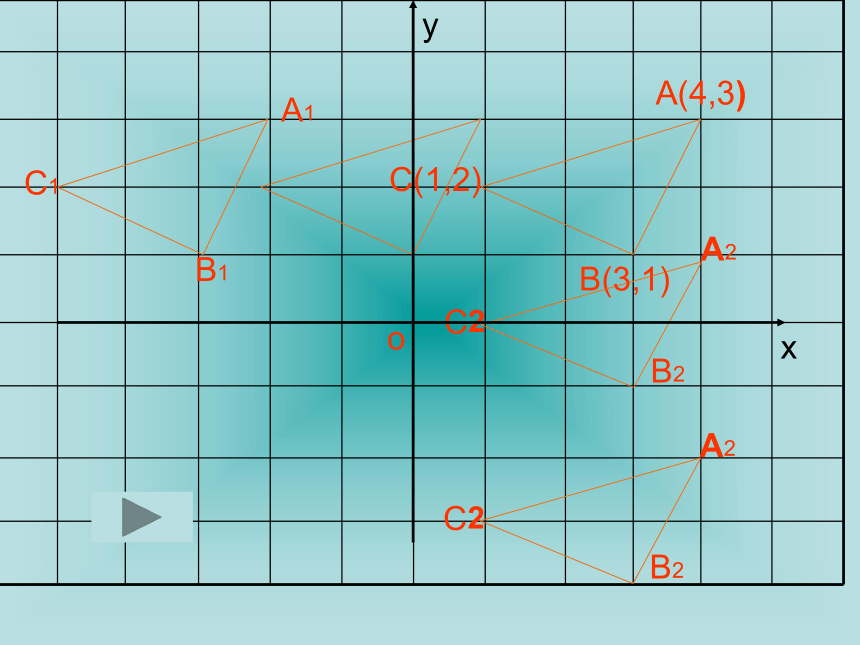
课件19张PPT。⒍⒉⒉ 用坐标表示平移问题2:(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1 、 C1.依次连接A1、B1 、 C1各点,所得三角形A1B1C1与三角形ABC在大小、形状和位置上有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A 2、B 2 、 C 2,依次连接A 2 、 B2 、 C2各点,所得三角形A2B2C2与三角形ABC在大小、形状和位置有什么关系? 三角形ABC三个顶点的坐标分别是A(4,3) B(3,1) C(1,2)。 在前面,我们学习了将一个点在坐标系中进行平移,那么我们将一个图形在平面直角坐标系中进行平移,它又会是什么样的呢?
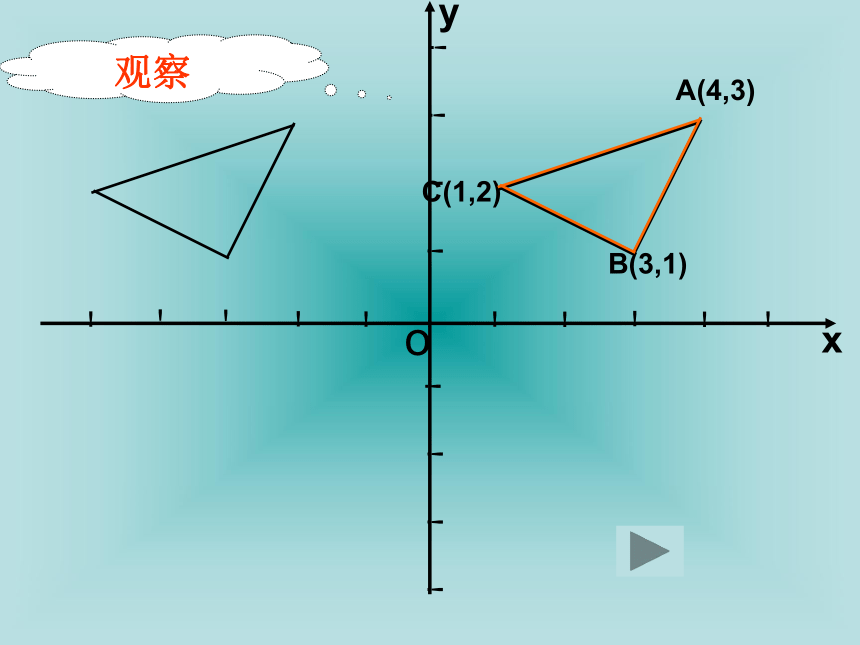
其实,将一个图形在平面直角坐标系中进行平移,这个图形的所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出这个图形进行了怎样的平移。A(4,3)B(3,1)C(1,2)探讨(1)如果将三角形ABC三个顶点A(4,3), B(3,1), C(1,2)的横坐标都加上3,能得出什么结论?若纵坐标都加上2,能得出什么结论?
(2)如果将三角形ABC三个顶点A(4,3), B(3,1), C(1,2)的横坐标都减去6,同时纵坐标都减去5,能得出什么结论?A(4,3)C(1,2)B(3,1)观察填空:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上 一个正数a,所得到的新图形就是把原图形向 平移 个单位长度;
如果把它各个点的纵坐标都加上 一个正数a,所得到的新图形就是把原图形向 平移 个单位长度;右a(或减去)(左)上a(或减去)(或向下)平面直角坐标系内平移图形的规律:概括成:上移加下移减 ,左移减右移加(纵坐标)(横坐标)11小试牛刀(一)、长方形ABCD的四个顶点坐标分别是A(-3,2)、B(-3,-2) 、 C(3,-2) 、 D(3,2),(二)三角形的三个顶点坐标分别是(-4,-1)、(1,1)、(-1,4),把这个三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是:
(-2,2)(3,4)(1,7)(1)把它向左平移2个单位长度后,四个顶点的坐标变成什么?(2)如果将它向上平移3个单位呢?(3)如果这个长方形的各个顶点的横坐标都加上2,纵坐标不变,这个长方形将怎样变化?如图,三架飞机P、Q、R保持编队飞行,请分别说出它们的坐标.
30秒后,飞机P飞到p`位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标。PQRP`我能行!
3.已知A(1,4),B(-4,0),C(2,0).
△ABC的面积是____.
4.将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
5.将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
6.若BC的坐标不变, △ABC的面积为6,点A的横坐标为-1,那么点A的坐标为________________.12(-2,4)(-7,0)(-1,0)(1,1)(-4,-3)(2,-3)(-1,2)或(-1,-2)例1例1 在平面直角坐标系内,将坐标为(1,1),(2,1),(2,2),(1,2),
(1,3),(2,3),的点依次连接起来,组成一个图形.(1)每个点的纵坐标不变,横坐标乘以2,再将所得的点依次连接起来,所得的图形与原图形相比有什么变化?(2)横坐标不变,纵坐标加3呢?解(1)变化后的每个点的坐标为(2,1),(4,1),(4,2),(2,2),(2,3),(4,3)(2)变化后的每个点的坐标为(1,4),(2,4),(2,5),(1,5),(1,6),(2,6)图象横向放大了2倍.图象整体向上平移了3个单位长度.回顾回顾纵坐标不变,横坐标乘以a, 意味着图像
. 横坐标不变,纵坐标加(或减去)a, 意味着图像
.横坐标不变,纵坐标乘以a, 意味着图像
. 纵坐标不变,横坐标加(或减去)a, 意味着图像
.整体向上(或向下)平移a个单位.整体向右(或向左)平移a个单位例2例2 将图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)
连接起来,并作以下变换:(1) 纵坐标不变,横坐标变为原来2倍,再将所得的点依次连接,所得的图形与原图形相比有什么变化?(2)纵坐标不变,横坐标分别加3呢?回顾回顾 了解点坐标变换与图形变化的关系,可以根据不同的需要对图形进行量身定做,加减乘除混合运算,可以达到任意转化的效果.探究探讨 在平面直角坐标系中,将坐标为 (0,3),(1,2)(3,3)(2,1)(2,-1)
(3,-3)(2,-2),(0,-3),(-1,-2),(-3,-3),(-2,-1),(-3,3),(-1,2),(0,3)的点用线段依次连接起来,形成一个图案.
(1)将各点的横坐标保持不变,纵坐标分别乘以-1,所得的图案与原图案相比有何变化?
(2)将各点的纵坐标保持不变,横坐标分别乘以-1,所得的图案与原图案相比有何变化?
(3)将各点的横坐标保持不变,纵坐标分别加2,所得的图案与原图案相比有何变化?
练习2 在三角形ABC中,A(2,4),B(-1,2),
C(1,-3),若把三角形ABC平移,
(1)使点A在坐标原点,求平移后B、C两点的坐标;
(2)使点B在坐标原点,求平移后A、C两点的坐标;
(3)使点C在坐标原点,求平移后A、B两点的坐标;
练习拓广探索(1)课本60页7题(2)课本66页5题本节课收获
再见
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A 2、B 2 、 C 2,依次连接A 2 、 B2 、 C2各点,所得三角形A2B2C2与三角形ABC在大小、形状和位置有什么关系? 三角形ABC三个顶点的坐标分别是A(4,3) B(3,1) C(1,2)。 在前面,我们学习了将一个点在坐标系中进行平移,那么我们将一个图形在平面直角坐标系中进行平移,它又会是什么样的呢?
其实,将一个图形在平面直角坐标系中进行平移,这个图形的所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出这个图形进行了怎样的平移。A(4,3)B(3,1)C(1,2)探讨(1)如果将三角形ABC三个顶点A(4,3), B(3,1), C(1,2)的横坐标都加上3,能得出什么结论?若纵坐标都加上2,能得出什么结论?
(2)如果将三角形ABC三个顶点A(4,3), B(3,1), C(1,2)的横坐标都减去6,同时纵坐标都减去5,能得出什么结论?A(4,3)C(1,2)B(3,1)观察填空:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上 一个正数a,所得到的新图形就是把原图形向 平移 个单位长度;
如果把它各个点的纵坐标都加上 一个正数a,所得到的新图形就是把原图形向 平移 个单位长度;右a(或减去)(左)上a(或减去)(或向下)平面直角坐标系内平移图形的规律:概括成:上移加下移减 ,左移减右移加(纵坐标)(横坐标)11小试牛刀(一)、长方形ABCD的四个顶点坐标分别是A(-3,2)、B(-3,-2) 、 C(3,-2) 、 D(3,2),(二)三角形的三个顶点坐标分别是(-4,-1)、(1,1)、(-1,4),把这个三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标分别是:
(-2,2)(3,4)(1,7)(1)把它向左平移2个单位长度后,四个顶点的坐标变成什么?(2)如果将它向上平移3个单位呢?(3)如果这个长方形的各个顶点的横坐标都加上2,纵坐标不变,这个长方形将怎样变化?如图,三架飞机P、Q、R保持编队飞行,请分别说出它们的坐标.
30秒后,飞机P飞到p`位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标。PQRP`我能行!
3.已知A(1,4),B(-4,0),C(2,0).
△ABC的面积是____.
4.将△ABC向左平移三个单位后,点A、B、C的坐标分别变为______,______,____.
5.将△ABC向下平移三个单位后,点A、B、C的坐标分别变为______,______,____.
6.若BC的坐标不变, △ABC的面积为6,点A的横坐标为-1,那么点A的坐标为________________.12(-2,4)(-7,0)(-1,0)(1,1)(-4,-3)(2,-3)(-1,2)或(-1,-2)例1例1 在平面直角坐标系内,将坐标为(1,1),(2,1),(2,2),(1,2),
(1,3),(2,3),的点依次连接起来,组成一个图形.(1)每个点的纵坐标不变,横坐标乘以2,再将所得的点依次连接起来,所得的图形与原图形相比有什么变化?(2)横坐标不变,纵坐标加3呢?解(1)变化后的每个点的坐标为(2,1),(4,1),(4,2),(2,2),(2,3),(4,3)(2)变化后的每个点的坐标为(1,4),(2,4),(2,5),(1,5),(1,6),(2,6)图象横向放大了2倍.图象整体向上平移了3个单位长度.回顾回顾纵坐标不变,横坐标乘以a, 意味着图像
. 横坐标不变,纵坐标加(或减去)a, 意味着图像
.横坐标不变,纵坐标乘以a, 意味着图像
. 纵坐标不变,横坐标加(或减去)a, 意味着图像
.整体向上(或向下)平移a个单位.整体向右(或向左)平移a个单位例2例2 将图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)
连接起来,并作以下变换:(1) 纵坐标不变,横坐标变为原来2倍,再将所得的点依次连接,所得的图形与原图形相比有什么变化?(2)纵坐标不变,横坐标分别加3呢?回顾回顾 了解点坐标变换与图形变化的关系,可以根据不同的需要对图形进行量身定做,加减乘除混合运算,可以达到任意转化的效果.探究探讨 在平面直角坐标系中,将坐标为 (0,3),(1,2)(3,3)(2,1)(2,-1)
(3,-3)(2,-2),(0,-3),(-1,-2),(-3,-3),(-2,-1),(-3,3),(-1,2),(0,3)的点用线段依次连接起来,形成一个图案.
(1)将各点的横坐标保持不变,纵坐标分别乘以-1,所得的图案与原图案相比有何变化?
(2)将各点的纵坐标保持不变,横坐标分别乘以-1,所得的图案与原图案相比有何变化?
(3)将各点的横坐标保持不变,纵坐标分别加2,所得的图案与原图案相比有何变化?
练习2 在三角形ABC中,A(2,4),B(-1,2),
C(1,-3),若把三角形ABC平移,
(1)使点A在坐标原点,求平移后B、C两点的坐标;
(2)使点B在坐标原点,求平移后A、C两点的坐标;
(3)使点C在坐标原点,求平移后A、B两点的坐标;
练习拓广探索(1)课本60页7题(2)课本66页5题本节课收获
再见
