2022—2023学年人教版数学八年级上册12.3 角的平分线的性质(2)同步练习 (含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册12.3 角的平分线的性质(2)同步练习 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 09:49:49 | ||
图片预览

文档简介
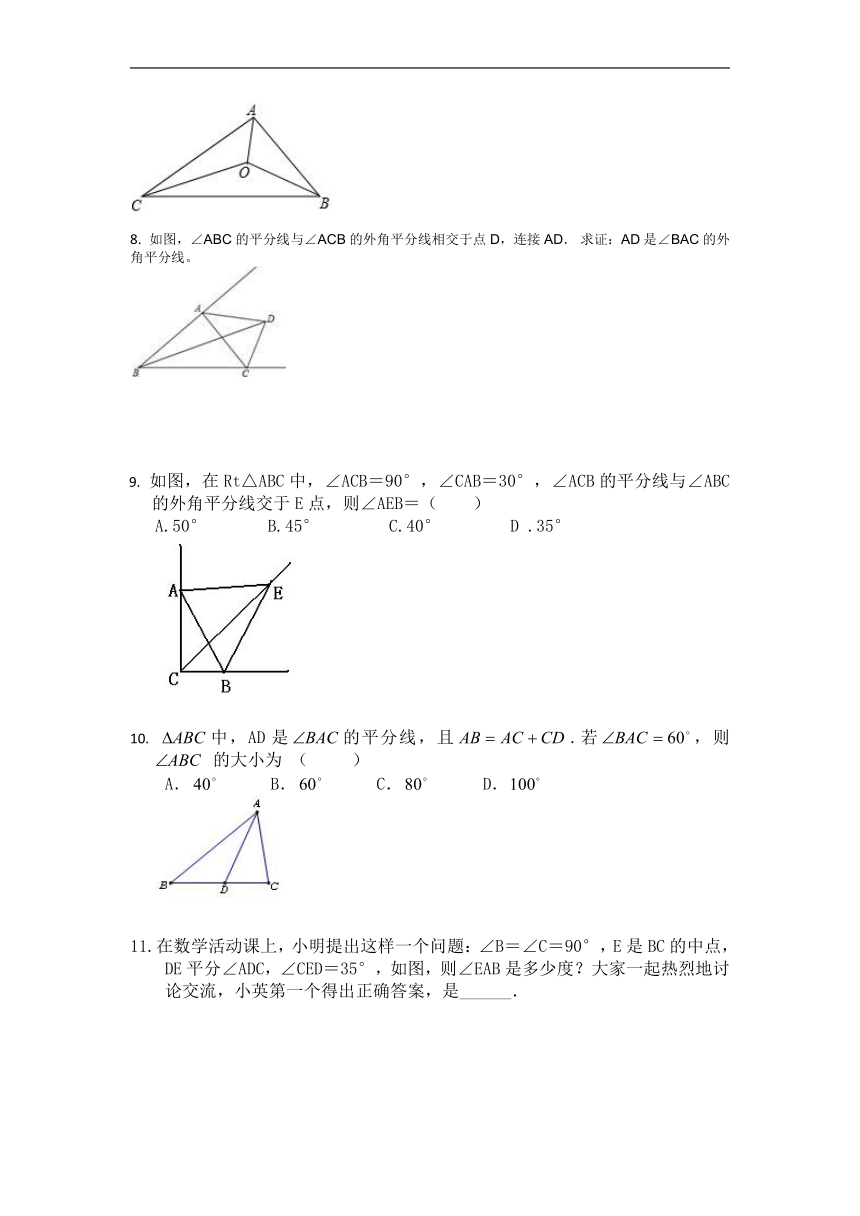
第2课时 角的平分线的判定
01基础题
知识点1 角的平分线的判定
1. 如图,PC⊥OA,PD⊥OB,当PC=PD时,Rt△OPC≌Rt△ ( ),
∴∠POC=∠ .
第1题图 第2题图
2.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=______.
3. 已知CD⊥AB于D,BE⊥AC于E,BE、CD相交于O
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
知识点2 兰角形的角平分线
4. 到△ABC的三条边距离相等的点是△ABC的( ).
A. 三条中线交点 B. 三条角平分线交点 C. 三条高的交点 D. 三条边的垂直平分线交点
5. 如图,点O到△ABC三边的距离相等,∠ABC=84°,则∠AOC=______.
知识点3 角的平分线的实际应用
6, 如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
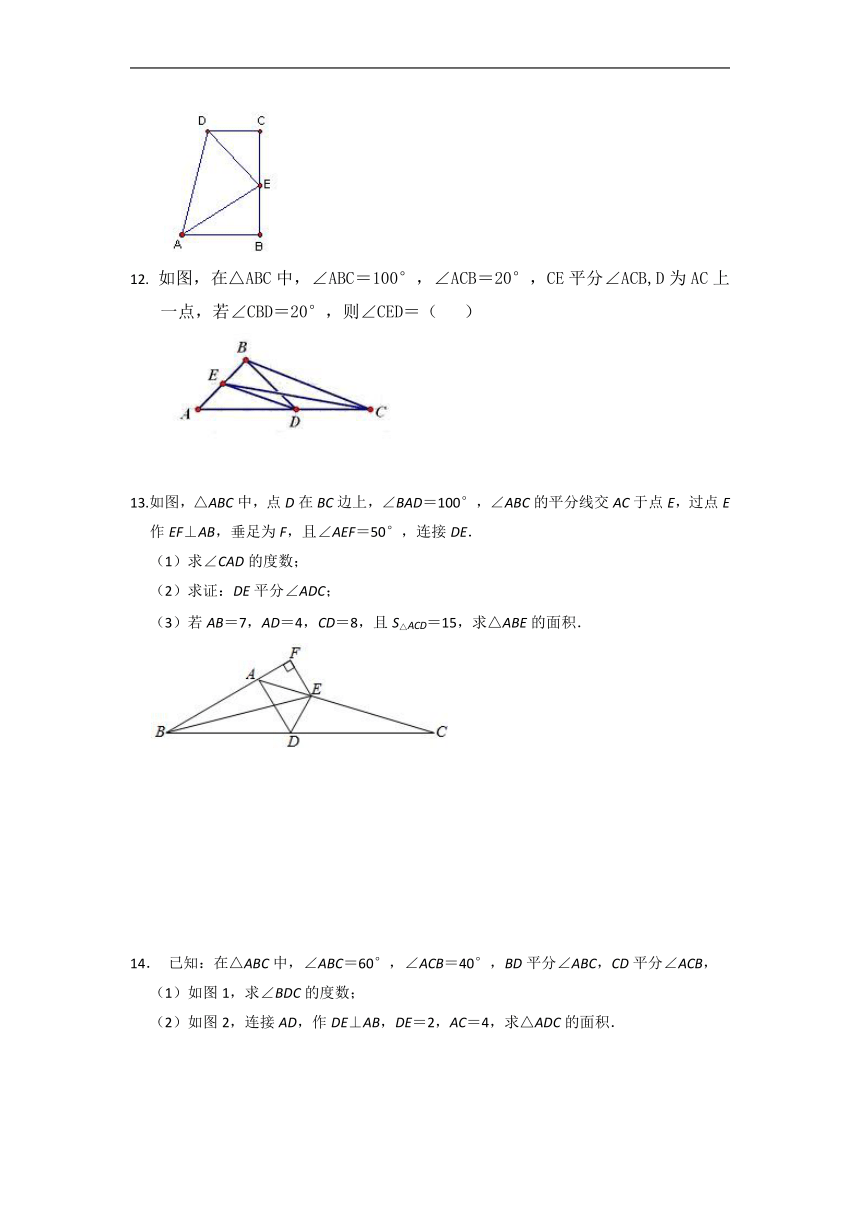
02中档题
7. 如图,△ABC的三边AB、AC、BC的长分别为4、6、8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OAC:S△OBC= 。
8. 如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD. 求证:AD是∠BAC的外角平分线。
9. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB=( )
A.50° B.45° C.40° D .35°
10. 中,AD是的平分线,且.若,则 的大小为 ( )
A. B. C. D.
11.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______.
12. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB,D为AC上一点,若∠CBD=20°,则∠CED=( )
13.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
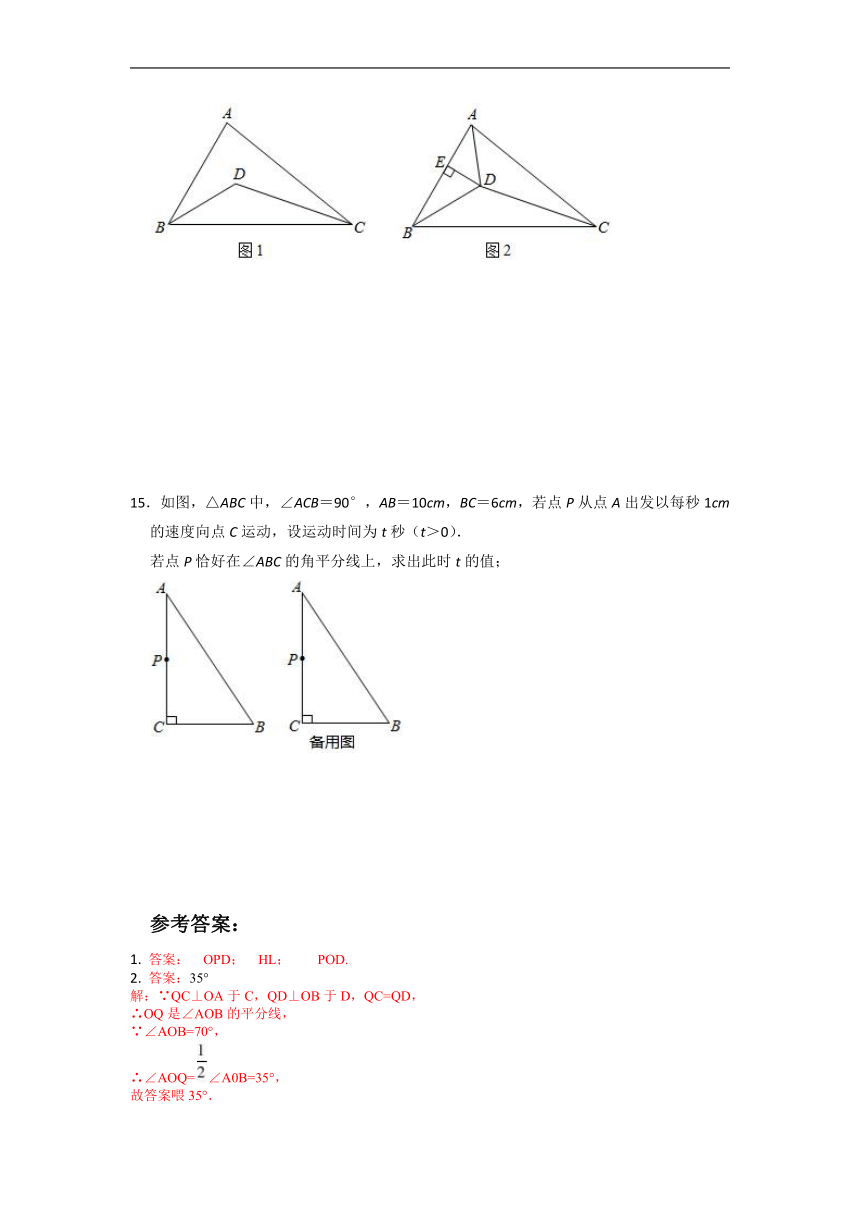
14. 已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
15.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
若点P恰好在∠ABC的角平分线上,求出此时t的值;
参考答案:
1. 答案: OPD; HL; POD.
2. 答案:35°
解:∵QC⊥OA于C,QD⊥OB于D,QC=QD,
∴OQ是∠AOB的平分线,
∵∠AOB=70°,
∴∠AOQ=∠A0B=35°,
故答案喂35°.
3. 分析:(1)若∠1=∠2,则OA是∠BAC的角平分线,根据角平分线的性质可得OD=OE;通过证△ODB≌△OEC,即可得出OB=OC的结论.
(2)与(1)的思路正好相反,若OB=OC,可证得△ODB≌△OEC,得OD=OE,根据角平分线的判定定理,即可得出∠1=∠2的结论.
解答:证明:(1)∵∠1=∠2,CD⊥AB,BE⊥AC,
∴OD=OE.
在△OBD和△OCE中
∴△OBD≌△OCE(AAS).
∴OB=OC.
(2)∵OB=OC,∠BOD=∠COE,∠ODB=∠OEC=90°,
∴△OBD≌△OCE(AAS).
∴OD=OE.
又∵OD⊥AB,OE⊥AC,垂足为D、E,
∴∠1=∠2.
点评:此题主要考查了全等三角形的判定和性质,以及角平分线的性质及判定定理.
4. 答案:B
[解析]试题分析:根据角平分线的判定定理,到角的两边距离相等的点在这个角的平分线上,所以到三角形三条边距离相等的点是三角形三条角平分线的交点.故本题选B.
考点:角平分线的判定定理的运用.
5. 答案:132°
6.作∠AOB的平分线交AB于M,即M为水厂的位置.
【解析】由已知条件,利用角的平分线上的点到角的两边的距离相等可知建在∠AOB的平分线与AB的交点上.
本题考点:角平分线的性质.
考点点评:本题主要考查角的平分线上的点到角的两边的距离相等的性质;一般的作图题要在图形上保留作图痕迹,此题的要求只要标出M就可,并非严格的作图题.
7. 答案:2:3:4
解:过点O作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,
∵O是三角形三条角平分线的交点,
∴OD=OE=OF,
∵AB=4,AC=6,BC=8,
∴S△OAB:S△OAC:S△OBC=2:3:4.
8. 证明:分别过D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,
∵BD平分∠CBE,DE⊥BE,DF⊥BC,
∴DE=DF.
同理DG=DF,
∴DE=DG,
∴点D在∠EAG平分线上,
∴AD是∠BAC的外角平分线.
本题主要考查角平分线的性质及判定.首先作辅助线:分别过D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,然后利用角的平分线上的点到角的两边的距离相等可知DE=DG,再利用到角两边距离相等的点在角的平分线上的逆定理证明.
9.答案:B
【解析】可证EA是∠CAB外角平分线.过点E作EF、EM、EN分别垂直于CB、AB、CA,并且交点分别为F、M、N,所以EF=EM=EN.所以EA是∠CAB的外角平分线
10. 答案:A
【解析】在AB边上截取AE=AC,连接DE,可证△ACD≌△AED,可推出CD=DE=BE,
2∠B=∠C,所以∠B=40°
11. 答案:
【解析】作EF⊥AD于F,证△DCE≌△DFE(HL),再证△AFE≌△ABE(HL),可得∠FEB=180°-70°=110°,∠AEB=55°,∠EAB=35°
12. 答案:10°
【解析】考虑△BDC中, EC 是∠C的平分线, EB是∠B的外角平分线, 所以E是△BDC的一个旁心, 于是ED平分∠BDA. ∠CED = ∠ADE - ∠DCE =∠ADB - ∠DCB =∠DBC = ×20°= 10°
13. 【分析】(1)根据直角三角形的性质求出∠FAE,根据补角的定义计算,得到答案;
(2)过点E作EG⊥AD于G,EH⊥BC于H,根据角平分线的性质得到EF=EG,EF=EH,等量代换得到EG=EH,根据角平分线的判定定理证明结论;
(3)根据三角形的面积公式求出EG,再根据三角形的面积公式计算,得到答案.
【解析】(1)解:∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EGCD×EH=15,即4×EG8×EG=15,
解得,EG=EH,
∴EF=EH,
∴△ABE的面积AB×EF7.
14. 【分析】(1)先根据角平分线的定义得到∠DBC=30°,∠DCB=20°,然后根据三角形内角和计算∠BDC的度数;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,根据角平分线的性质得到DH=DE=DF=2,然后根据三角形面积公式计算△ADC的面积.
【解析】解:(1)∵BD平分∠ABC,
∴∠DBC∠ABC60°=30°,
∵CD平分∠ACB,
∴∠DCB∠ACB40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积DF AC2×4=4.
15.【分析】(1)作PD⊥AB于D,如图,AP=t,先利用勾股定理计算出AC=8,再根据角平分线的性质得到PC=PD=8﹣t,利用三角形面积公式得到10×(8﹣t)6×(8﹣t)6×8,然后解方程即可;
【解析】解:(1)作PD⊥AB于D,如图,AP=t,
∵∠ACB=90°,AB=10,BC=6,
∴AC8,
∵BP平分∠ABC,
∴PC=PD=8﹣t,
∵S△ABP+S△BCP=S△ABC,
∴10×(8﹣t)6×(8﹣t)6×8,
解得t=5,
即此时t的值为5s;
01基础题
知识点1 角的平分线的判定
1. 如图,PC⊥OA,PD⊥OB,当PC=PD时,Rt△OPC≌Rt△ ( ),
∴∠POC=∠ .
第1题图 第2题图
2.如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=______.
3. 已知CD⊥AB于D,BE⊥AC于E,BE、CD相交于O
求证:(1)当∠1=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
知识点2 兰角形的角平分线
4. 到△ABC的三条边距离相等的点是△ABC的( ).
A. 三条中线交点 B. 三条角平分线交点 C. 三条高的交点 D. 三条边的垂直平分线交点
5. 如图,点O到△ABC三边的距离相等,∠ABC=84°,则∠AOC=______.
知识点3 角的平分线的实际应用
6, 如图,铁路OA和铁路OB交于O处,河道AB与铁路分别交于A处和B处,试在河岸上建一座水厂M,要求M到铁路OA,OB的距离相等,则该水厂M应建在图中什么位置?请在图中标出M点的位置.
02中档题
7. 如图,△ABC的三边AB、AC、BC的长分别为4、6、8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OAC:S△OBC= 。
8. 如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD. 求证:AD是∠BAC的外角平分线。
9. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=30°,∠ACB的平分线与∠ABC的外角平分线交于E点,则∠AEB=( )
A.50° B.45° C.40° D .35°
10. 中,AD是的平分线,且.若,则 的大小为 ( )
A. B. C. D.
11.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______.
12. 如图,在△ABC中,∠ABC=100°,∠ACB=20°,CE平分∠ACB,D为AC上一点,若∠CBD=20°,则∠CED=( )
13.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
14. 已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
15.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发以每秒1cm的速度向点C运动,设运动时间为t秒(t>0).
若点P恰好在∠ABC的角平分线上,求出此时t的值;
参考答案:
1. 答案: OPD; HL; POD.
2. 答案:35°
解:∵QC⊥OA于C,QD⊥OB于D,QC=QD,
∴OQ是∠AOB的平分线,
∵∠AOB=70°,
∴∠AOQ=∠A0B=35°,
故答案喂35°.
3. 分析:(1)若∠1=∠2,则OA是∠BAC的角平分线,根据角平分线的性质可得OD=OE;通过证△ODB≌△OEC,即可得出OB=OC的结论.
(2)与(1)的思路正好相反,若OB=OC,可证得△ODB≌△OEC,得OD=OE,根据角平分线的判定定理,即可得出∠1=∠2的结论.
解答:证明:(1)∵∠1=∠2,CD⊥AB,BE⊥AC,
∴OD=OE.
在△OBD和△OCE中
∴△OBD≌△OCE(AAS).
∴OB=OC.
(2)∵OB=OC,∠BOD=∠COE,∠ODB=∠OEC=90°,
∴△OBD≌△OCE(AAS).
∴OD=OE.
又∵OD⊥AB,OE⊥AC,垂足为D、E,
∴∠1=∠2.
点评:此题主要考查了全等三角形的判定和性质,以及角平分线的性质及判定定理.
4. 答案:B
[解析]试题分析:根据角平分线的判定定理,到角的两边距离相等的点在这个角的平分线上,所以到三角形三条边距离相等的点是三角形三条角平分线的交点.故本题选B.
考点:角平分线的判定定理的运用.
5. 答案:132°
6.作∠AOB的平分线交AB于M,即M为水厂的位置.
【解析】由已知条件,利用角的平分线上的点到角的两边的距离相等可知建在∠AOB的平分线与AB的交点上.
本题考点:角平分线的性质.
考点点评:本题主要考查角的平分线上的点到角的两边的距离相等的性质;一般的作图题要在图形上保留作图痕迹,此题的要求只要标出M就可,并非严格的作图题.
7. 答案:2:3:4
解:过点O作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,
∵O是三角形三条角平分线的交点,
∴OD=OE=OF,
∵AB=4,AC=6,BC=8,
∴S△OAB:S△OAC:S△OBC=2:3:4.
8. 证明:分别过D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,
∵BD平分∠CBE,DE⊥BE,DF⊥BC,
∴DE=DF.
同理DG=DF,
∴DE=DG,
∴点D在∠EAG平分线上,
∴AD是∠BAC的外角平分线.
本题主要考查角平分线的性质及判定.首先作辅助线:分别过D作DE、DF、DG垂直于AB、BC、AC,垂足分别为E、F、G,然后利用角的平分线上的点到角的两边的距离相等可知DE=DG,再利用到角两边距离相等的点在角的平分线上的逆定理证明.
9.答案:B
【解析】可证EA是∠CAB外角平分线.过点E作EF、EM、EN分别垂直于CB、AB、CA,并且交点分别为F、M、N,所以EF=EM=EN.所以EA是∠CAB的外角平分线
10. 答案:A
【解析】在AB边上截取AE=AC,连接DE,可证△ACD≌△AED,可推出CD=DE=BE,
2∠B=∠C,所以∠B=40°
11. 答案:
【解析】作EF⊥AD于F,证△DCE≌△DFE(HL),再证△AFE≌△ABE(HL),可得∠FEB=180°-70°=110°,∠AEB=55°,∠EAB=35°
12. 答案:10°
【解析】考虑△BDC中, EC 是∠C的平分线, EB是∠B的外角平分线, 所以E是△BDC的一个旁心, 于是ED平分∠BDA. ∠CED = ∠ADE - ∠DCE =∠ADB - ∠DCB =∠DBC = ×20°= 10°
13. 【分析】(1)根据直角三角形的性质求出∠FAE,根据补角的定义计算,得到答案;
(2)过点E作EG⊥AD于G,EH⊥BC于H,根据角平分线的性质得到EF=EG,EF=EH,等量代换得到EG=EH,根据角平分线的判定定理证明结论;
(3)根据三角形的面积公式求出EG,再根据三角形的面积公式计算,得到答案.
【解析】(1)解:∵EF⊥AB,∠AEF=50°,
∴∠FAE=90°﹣50°=40°,
∵∠BAD=100°,
∴∠CAD=180°﹣100°﹣40°=40°;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵∠FAE=∠DAE=40°,EF⊥BF,EG⊥AD,
∴EF=EG,
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵S△ACD=15,
∴AD×EGCD×EH=15,即4×EG8×EG=15,
解得,EG=EH,
∴EF=EH,
∴△ABE的面积AB×EF7.
14. 【分析】(1)先根据角平分线的定义得到∠DBC=30°,∠DCB=20°,然后根据三角形内角和计算∠BDC的度数;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,根据角平分线的性质得到DH=DE=DF=2,然后根据三角形面积公式计算△ADC的面积.
【解析】解:(1)∵BD平分∠ABC,
∴∠DBC∠ABC60°=30°,
∵CD平分∠ACB,
∴∠DCB∠ACB40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积DF AC2×4=4.
15.【分析】(1)作PD⊥AB于D,如图,AP=t,先利用勾股定理计算出AC=8,再根据角平分线的性质得到PC=PD=8﹣t,利用三角形面积公式得到10×(8﹣t)6×(8﹣t)6×8,然后解方程即可;
【解析】解:(1)作PD⊥AB于D,如图,AP=t,
∵∠ACB=90°,AB=10,BC=6,
∴AC8,
∵BP平分∠ABC,
∴PC=PD=8﹣t,
∵S△ABP+S△BCP=S△ABC,
∴10×(8﹣t)6×(8﹣t)6×8,
解得t=5,
即此时t的值为5s;
