2022—2023学年人教版数学八年级上册12.2 三角形全等的判定二(SAS) 同步练习(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级上册12.2 三角形全等的判定二(SAS) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 00:00:00 | ||
图片预览


文档简介
第2课时 用“SAS”判定三角形全等
01基础题
知识点1 用“SAS”判定三角形全等
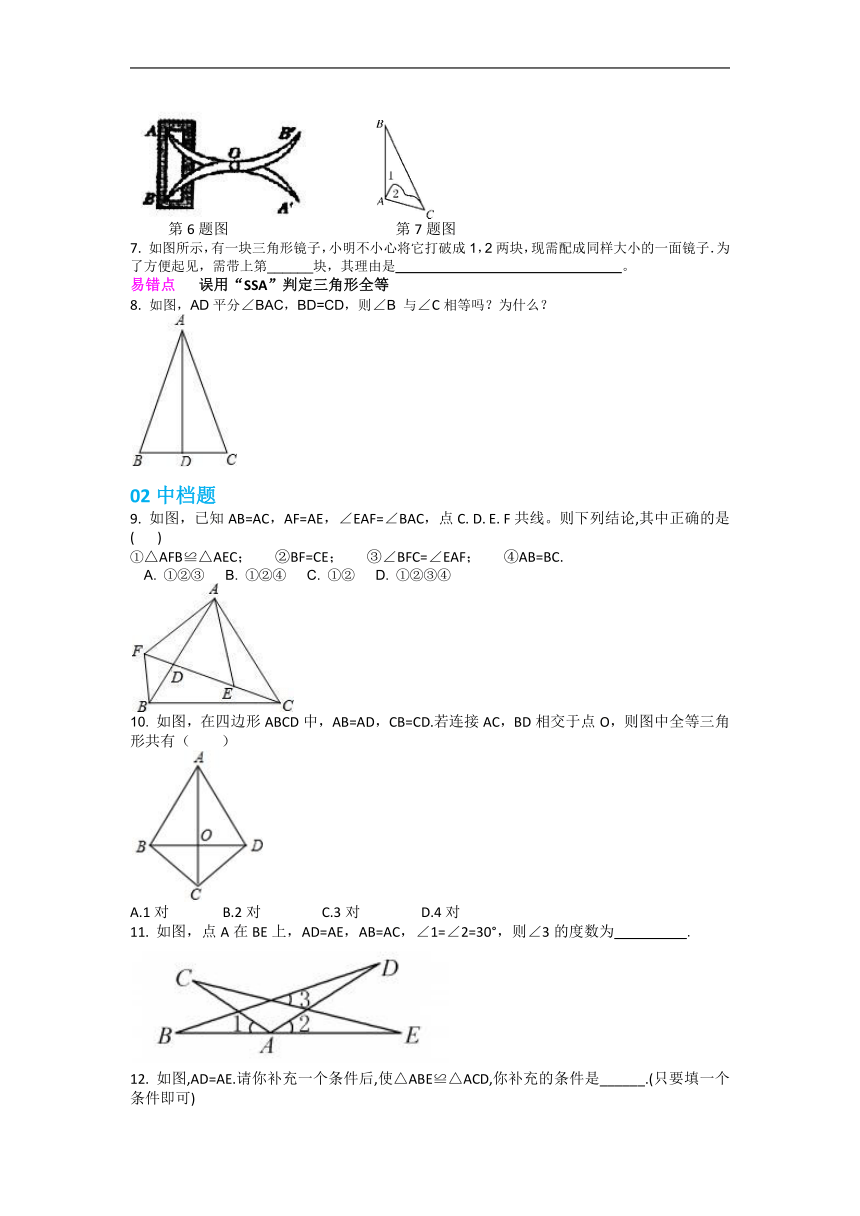
1.下图中全等的三角形有( )
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
2. 如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件( )
A.DB=CB B.AB=AB C.AD=AC D.∠D=∠C
3. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
知识点2 三角形全等的判定与性质的综合
4. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
5. 如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.
知识点3 用“SAS”判定三角形全等解决实际问题
6. 如图,将两根钢条 AA' 、 BB' 的中点O连在一起,使 AA' 、 BB' 能绕着点O自由转动就做成了一个测量工具,则 A'B' 的长等于内槽宽AB,那么判定 ΔOAB ΔOA'B' 的理由是 (写简称)。
第6题图 第7题图
7. 如图所示,有一块三角形镜子,小明不小心将它打破成1,2两块,现需配成同样大小的一面镜子.为了方便起见,需带上第______块,其理由是 。
易错点 误用“SSA”判定三角形全等
8. 如图,AD平分∠BAC,BD=CD,则∠B 与∠C相等吗?为什么?
02中档题
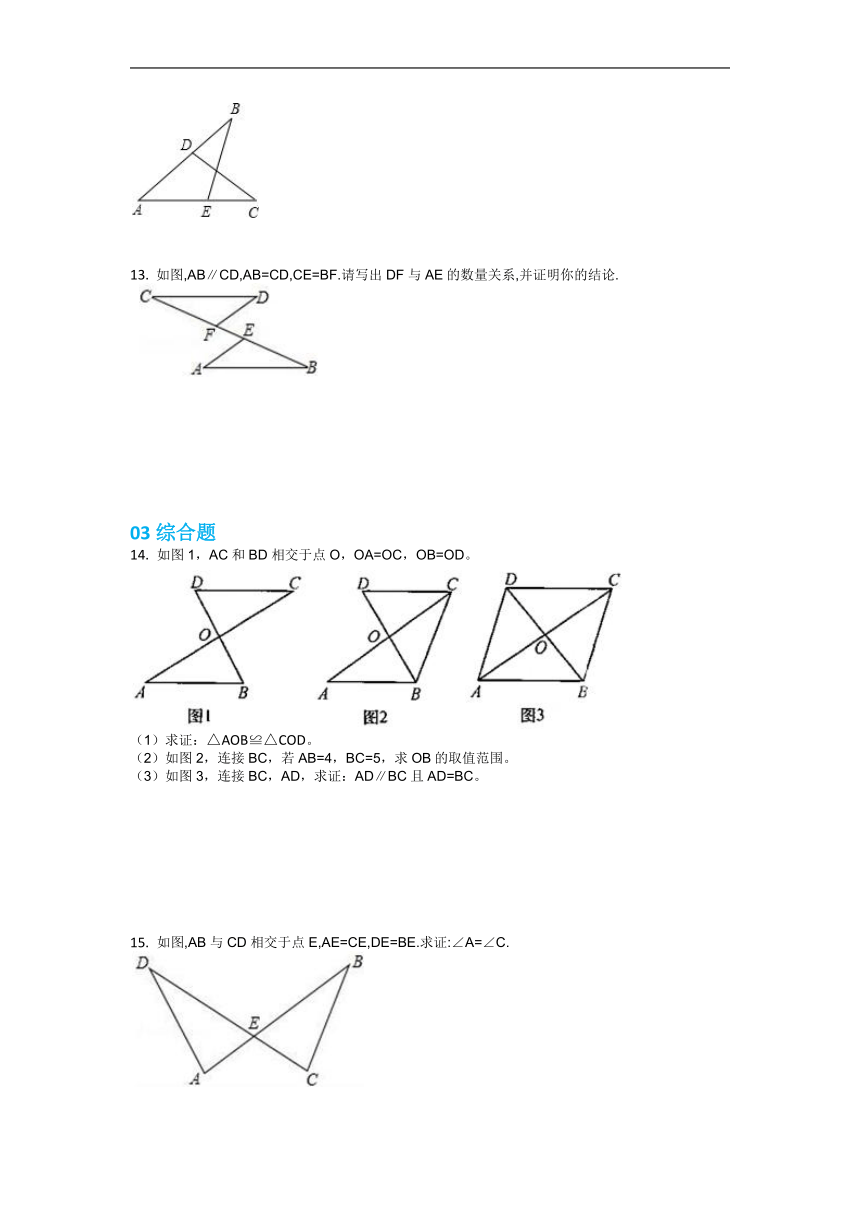
9. 如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C. D. E. F共线。则下列结论,其中正确的是( )
①△AFB≌△AEC; ②BF=CE; ③∠BFC=∠EAF; ④AB=BC.
A. ①②③ B. ①②④ C. ①② D. ①②③④
10. 如图,在四边形ABCD中,AB=AD,CB=CD.若连接AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
11. 如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 .
12. 如图,AD=AE.请你补充一个条件后,使△ABE≌△ACD,你补充的条件是______.(只要填一个条件即可)
13. 如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
03综合题
14. 如图1,AC和BD相交于点O,OA=OC,OB=OD。
(1)求证:△AOB≌△COD。
(2)如图2,连接BC,若AB=4,BC=5,求OB的取值范围。
(3)如图3,连接BC,AD,求证:AD∥BC且AD=BC。
15. 如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
参考答案:
1. 答案:D
2. 答案:C
分析:根据角平分线得出∠CAB=∠DAB,隐含条件AB=AB,根据全等三角形的判定定理判断即可.
解答:解:∵AB平分∠DAC,∴∠CAB=∠DAB,
A、根据DB=CB,BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
B、根据BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
C、∵在△CAB和△DAB中 ∴△CAB≌△DAB(SAS),故本选项正确;
D、根据BA=BA,∠CAB=∠DAB,∠D=∠C,根据AAS可证△CAB≌△DAB,根据本选项错误;
故选C.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
3. 分析 根据全等三角形的判定即可求证:△ADF≌△BCE
解答 解:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,
∴△ADF≌△BCE(SAS)
点评 本题考查全等三角形的判定,解题的关键是求证AF=BE,本题属于基础题型.
4. 分析 由CD∥BE,可证得∠ACD=∠B,然后由C是线段AB的中点,CD=BE,利用SAS即可证得△ACD≌△CBE,继而证得结论.
解答 证明:∵C是线段AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS),
∴∠D=∠E.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意证得△ACD≌△CBE是关键.
5. 分析 根据全等三角形的判定定理得出△AOD≌△COB,推出AD=BC,∠DAO=∠CBO,根据平行线的判定得出即可.
解答 证明:在△AOD和△COB中,
∴△AOD≌△COB(SAS),
∴AD=BC,∠DAO=∠CBO,
∴AD∥BC.
点评 本题考查了全等三角形的性质和判定,平行线的判定的应用,能推出△AOD≌△COB是解此题的关键.
6. 答案:SAS
解:∵O是AA′、BB′的中点,∴AO=A′O,BO=B′O,在△OAB和△OA′B′中
AO=A′O,∠AOB=∠A′OB′,BO=B′O ,
∴△OAB≌△OA′B′(SAS).
故答案为:SAS.
由O是AA′、BB′的中点,可得AO=A′O,BO=B′O,再有∠AOB=∠A′OB′,可以根据全等三角形的判定方法SAS,判定△OAB≌△OA′B′.
此题主要考查了全等三角形的应用,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL,要证明两个三角形全等,必须有对应边相等这一条件.
7. 答案:1 两边及其夹角对应相等的两个三角形全等.
8. 解:相等,理由:
因为AD平分∠BAC ,
所以∠BAD =∠CAD .
在△ABD和△ACD 中,
∴△ABD≌△ACD
∴∠B=∠C
以上解答是否正确?若不正确,请说明理由.
以上解答不正确,理由如下:
在△ABD和△ACD 中,BD=CD,AD=AD,∠BAD =∠CAD ,
不能判定
当两个三角形有两边及一角对应相等时,只有该角是两边的夹角时才能判定两个三角形全等;
正确解法如下:延长AD至E,使AD=DE,连接BE
在△ADC和△EDB 中,
,
∴△ADC≌△EDB,
∴BE=AC ∠DAC =∠DEB,
∵AD,平分∠BAC,
∴∠BAD =∠CAD,
∴∠BAD =∠BED,
∴AB=BE,
∴AB=AC,
∴∠B=∠C.
9.答案:A
∵∠EAF=∠BAC,
∴∠BAF=∠CAE,
∵AF=AE,AB=AC,
∴△FAB≌△EAC(SAS),故①正确,
∴BF=EC,故②正确,
∴∠ABF=∠ACE,
∵∠BDF=∠ADC,
∴∠BFC=∠DAC,∵∠DAC=∠EAF,
∴∠BFC=∠EAF,故③正确,
无法判断AB=BC,故④错误,
故选:A.
想办法证明△FAB≌△EAC(SAS),利用全等三角形的性质即可解决问题;
10. 答案:C.
解:∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AO=AO,
∴△ABO≌△ADO,
同理可得△CBO≌△CDO,
故选C.
【考点提示】
本题主要是全等三角形的判定问题,回顾一下,全等三角形的判定方法;
【解题方法提示】
先找出图中的三角形有△ABC、△ADC、△ABD、△ACD、△ABO、△ADO、△CBO、△CDO;
再由已知条件可知AB=AD,CB=CD,AC=AC,AO=AO、CO=CO,再运用全等三角形的判定即可求解.
11. 答案:30°.
∵∠1=∠2=30°,
∴∠BAD=∠CAE.
在△BAD与△CAE中,
∵
∴△BAD≌△CAE,
∴∠D=∠E,
∵∠1=∠2=30°,
∴∠B+∠D=30°,
∴∠3=∠B+∠E=∠B+∠D=30°.
【考点提示】
本题考查了三角形全等的判定和性质,证明△BAD≌△CAE是解题的关键;
【解题方法提示】
首先,根据AD=AE,AB=AC,∠1=∠2=30°,则∠BAD=∠CAE,可证得△BAD≌△CAE(SAS);
接下来利用全等三角形的对应角相等,可得∠D=∠E,然后利用三角形外角等于与它不相邻的两个内角和,即可求得∠3的度数.
12. 答案:AB=AC
添加条件是AB=AC,
理由是:∵在△ABE和△ACD中
∵
∴△ABE≌△ACD,
故答案为:AB=AC.
此题是一道开放性的题目,答案不唯一,如AB=AC或∠B=∠C,或∠AEB=∠ADC.
13. [分析]结论:DF=AE.只要证明△CDF≌△BAE即可;
[解答]解:结论:DF=AE.
理由:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CF=BE,∵CD=AB,
∴△CDF≌△BAE,(SAS)
∴DF=AE.
14.(1)证明:在△AOB和△COD 中
∵
∴△AOB≌△COD(SAS)
(2)∵△AOB≌△COD
∴CD=AB=4,
∵BC=5
∴BC-CD∴5-4∴1∵OB=OD
∴(3) ∵OA=OC, OB=OD
∴四边形ABCD是平行四边形,
∴AD//BC, AD=BC
15. [分析]根据AE=EC,DE=BE,∠AED和∠CEB是对顶角,利用SAS证明△ADE≌△CBE即可.
[解答]证明:在△AED和△CEB中,
∴△AED≌△CEB〔SAS〕,
∴∠A=∠C〔全等三角形对应角相等〕.
01基础题
知识点1 用“SAS”判定三角形全等
1.下图中全等的三角形有( )
A.Ⅰ和Ⅱ B.Ⅱ和Ⅳ C.Ⅱ和Ⅲ D.Ⅰ和Ⅲ
2. 如图,AB平分∠DAC,要用SAS条件确定△ABC≌△ABD,还需要有条件( )
A.DB=CB B.AB=AB C.AD=AC D.∠D=∠C
3. 如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:△ADF≌△BCE.
知识点2 三角形全等的判定与性质的综合
4. 如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.
5. 如图,AO=CO,BO=DO,求证:AD=BC,AD∥BC.
知识点3 用“SAS”判定三角形全等解决实际问题
6. 如图,将两根钢条 AA' 、 BB' 的中点O连在一起,使 AA' 、 BB' 能绕着点O自由转动就做成了一个测量工具,则 A'B' 的长等于内槽宽AB,那么判定 ΔOAB ΔOA'B' 的理由是 (写简称)。
第6题图 第7题图
7. 如图所示,有一块三角形镜子,小明不小心将它打破成1,2两块,现需配成同样大小的一面镜子.为了方便起见,需带上第______块,其理由是 。
易错点 误用“SSA”判定三角形全等
8. 如图,AD平分∠BAC,BD=CD,则∠B 与∠C相等吗?为什么?
02中档题
9. 如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C. D. E. F共线。则下列结论,其中正确的是( )
①△AFB≌△AEC; ②BF=CE; ③∠BFC=∠EAF; ④AB=BC.
A. ①②③ B. ①②④ C. ①② D. ①②③④
10. 如图,在四边形ABCD中,AB=AD,CB=CD.若连接AC,BD相交于点O,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
11. 如图,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为 .
12. 如图,AD=AE.请你补充一个条件后,使△ABE≌△ACD,你补充的条件是______.(只要填一个条件即可)
13. 如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.
03综合题
14. 如图1,AC和BD相交于点O,OA=OC,OB=OD。
(1)求证:△AOB≌△COD。
(2)如图2,连接BC,若AB=4,BC=5,求OB的取值范围。
(3)如图3,连接BC,AD,求证:AD∥BC且AD=BC。
15. 如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.
参考答案:
1. 答案:D
2. 答案:C
分析:根据角平分线得出∠CAB=∠DAB,隐含条件AB=AB,根据全等三角形的判定定理判断即可.
解答:解:∵AB平分∠DAC,∴∠CAB=∠DAB,
A、根据DB=CB,BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
B、根据BA=BA,∠CAB=∠DAB不能推出两三角形全等,故本选项错误;
C、∵在△CAB和△DAB中 ∴△CAB≌△DAB(SAS),故本选项正确;
D、根据BA=BA,∠CAB=∠DAB,∠D=∠C,根据AAS可证△CAB≌△DAB,根据本选项错误;
故选C.
点评:本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
3. 分析 根据全等三角形的判定即可求证:△ADF≌△BCE
解答 解:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
在△ADF与△BCE中,
∴△ADF≌△BCE(SAS)
点评 本题考查全等三角形的判定,解题的关键是求证AF=BE,本题属于基础题型.
4. 分析 由CD∥BE,可证得∠ACD=∠B,然后由C是线段AB的中点,CD=BE,利用SAS即可证得△ACD≌△CBE,继而证得结论.
解答 证明:∵C是线段AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B,
在△ACD和△CBE中,
∴△ACD≌△CBE(SAS),
∴∠D=∠E.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意证得△ACD≌△CBE是关键.
5. 分析 根据全等三角形的判定定理得出△AOD≌△COB,推出AD=BC,∠DAO=∠CBO,根据平行线的判定得出即可.
解答 证明:在△AOD和△COB中,
∴△AOD≌△COB(SAS),
∴AD=BC,∠DAO=∠CBO,
∴AD∥BC.
点评 本题考查了全等三角形的性质和判定,平行线的判定的应用,能推出△AOD≌△COB是解此题的关键.
6. 答案:SAS
解:∵O是AA′、BB′的中点,∴AO=A′O,BO=B′O,在△OAB和△OA′B′中
AO=A′O,∠AOB=∠A′OB′,BO=B′O ,
∴△OAB≌△OA′B′(SAS).
故答案为:SAS.
由O是AA′、BB′的中点,可得AO=A′O,BO=B′O,再有∠AOB=∠A′OB′,可以根据全等三角形的判定方法SAS,判定△OAB≌△OA′B′.
此题主要考查了全等三角形的应用,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL,要证明两个三角形全等,必须有对应边相等这一条件.
7. 答案:1 两边及其夹角对应相等的两个三角形全等.
8. 解:相等,理由:
因为AD平分∠BAC ,
所以∠BAD =∠CAD .
在△ABD和△ACD 中,
∴△ABD≌△ACD
∴∠B=∠C
以上解答是否正确?若不正确,请说明理由.
以上解答不正确,理由如下:
在△ABD和△ACD 中,BD=CD,AD=AD,∠BAD =∠CAD ,
不能判定
当两个三角形有两边及一角对应相等时,只有该角是两边的夹角时才能判定两个三角形全等;
正确解法如下:延长AD至E,使AD=DE,连接BE
在△ADC和△EDB 中,
,
∴△ADC≌△EDB,
∴BE=AC ∠DAC =∠DEB,
∵AD,平分∠BAC,
∴∠BAD =∠CAD,
∴∠BAD =∠BED,
∴AB=BE,
∴AB=AC,
∴∠B=∠C.
9.答案:A
∵∠EAF=∠BAC,
∴∠BAF=∠CAE,
∵AF=AE,AB=AC,
∴△FAB≌△EAC(SAS),故①正确,
∴BF=EC,故②正确,
∴∠ABF=∠ACE,
∵∠BDF=∠ADC,
∴∠BFC=∠DAC,∵∠DAC=∠EAF,
∴∠BFC=∠EAF,故③正确,
无法判断AB=BC,故④错误,
故选:A.
想办法证明△FAB≌△EAC(SAS),利用全等三角形的性质即可解决问题;
10. 答案:C.
解:∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AO=AO,
∴△ABO≌△ADO,
同理可得△CBO≌△CDO,
故选C.
【考点提示】
本题主要是全等三角形的判定问题,回顾一下,全等三角形的判定方法;
【解题方法提示】
先找出图中的三角形有△ABC、△ADC、△ABD、△ACD、△ABO、△ADO、△CBO、△CDO;
再由已知条件可知AB=AD,CB=CD,AC=AC,AO=AO、CO=CO,再运用全等三角形的判定即可求解.
11. 答案:30°.
∵∠1=∠2=30°,
∴∠BAD=∠CAE.
在△BAD与△CAE中,
∵
∴△BAD≌△CAE,
∴∠D=∠E,
∵∠1=∠2=30°,
∴∠B+∠D=30°,
∴∠3=∠B+∠E=∠B+∠D=30°.
【考点提示】
本题考查了三角形全等的判定和性质,证明△BAD≌△CAE是解题的关键;
【解题方法提示】
首先,根据AD=AE,AB=AC,∠1=∠2=30°,则∠BAD=∠CAE,可证得△BAD≌△CAE(SAS);
接下来利用全等三角形的对应角相等,可得∠D=∠E,然后利用三角形外角等于与它不相邻的两个内角和,即可求得∠3的度数.
12. 答案:AB=AC
添加条件是AB=AC,
理由是:∵在△ABE和△ACD中
∵
∴△ABE≌△ACD,
故答案为:AB=AC.
此题是一道开放性的题目,答案不唯一,如AB=AC或∠B=∠C,或∠AEB=∠ADC.
13. [分析]结论:DF=AE.只要证明△CDF≌△BAE即可;
[解答]解:结论:DF=AE.
理由:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CF=BE,∵CD=AB,
∴△CDF≌△BAE,(SAS)
∴DF=AE.
14.(1)证明:在△AOB和△COD 中
∵
∴△AOB≌△COD(SAS)
(2)∵△AOB≌△COD
∴CD=AB=4,
∵BC=5
∴BC-CD
∴
∴四边形ABCD是平行四边形,
∴AD//BC, AD=BC
15. [分析]根据AE=EC,DE=BE,∠AED和∠CEB是对顶角,利用SAS证明△ADE≌△CBE即可.
[解答]证明:在△AED和△CEB中,
∴△AED≌△CEB〔SAS〕,
∴∠A=∠C〔全等三角形对应角相等〕.
