2022-2023学年上学期小学数学人教新版五年级同步经典题精练之多边形的面积综合题(含答案)
文档属性
| 名称 | 2022-2023学年上学期小学数学人教新版五年级同步经典题精练之多边形的面积综合题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 318.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 19:30:45 | ||
图片预览


文档简介
2022-2023学年上学期小学数学人教新版五年级同步经典题精练之多边形的面积综合题
一.选择题(共9小题)
1.如果把一个平行四边形活动框架拉成一个长方形,那么( )
A.周长和面积都不变 B.周长不变,面积变大
C.周长变大,面积不变 D.周长不变,面积变小
2.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是4cm,三角形的高是( )
A.2cm B.4cm C.8cm D.12cm
3.有一堆钢管,最上层摆6根,最下层摆10根,每一层比上一层多1根,这堆钢管共有( )根。
A.40 B.50 C.60 D.80
4.如图,平行线间三个阴影图形的面积关系是( )(单位:cm)
A.平行四边形的面积最大 B.梯形的面积最大
C.面积都相等
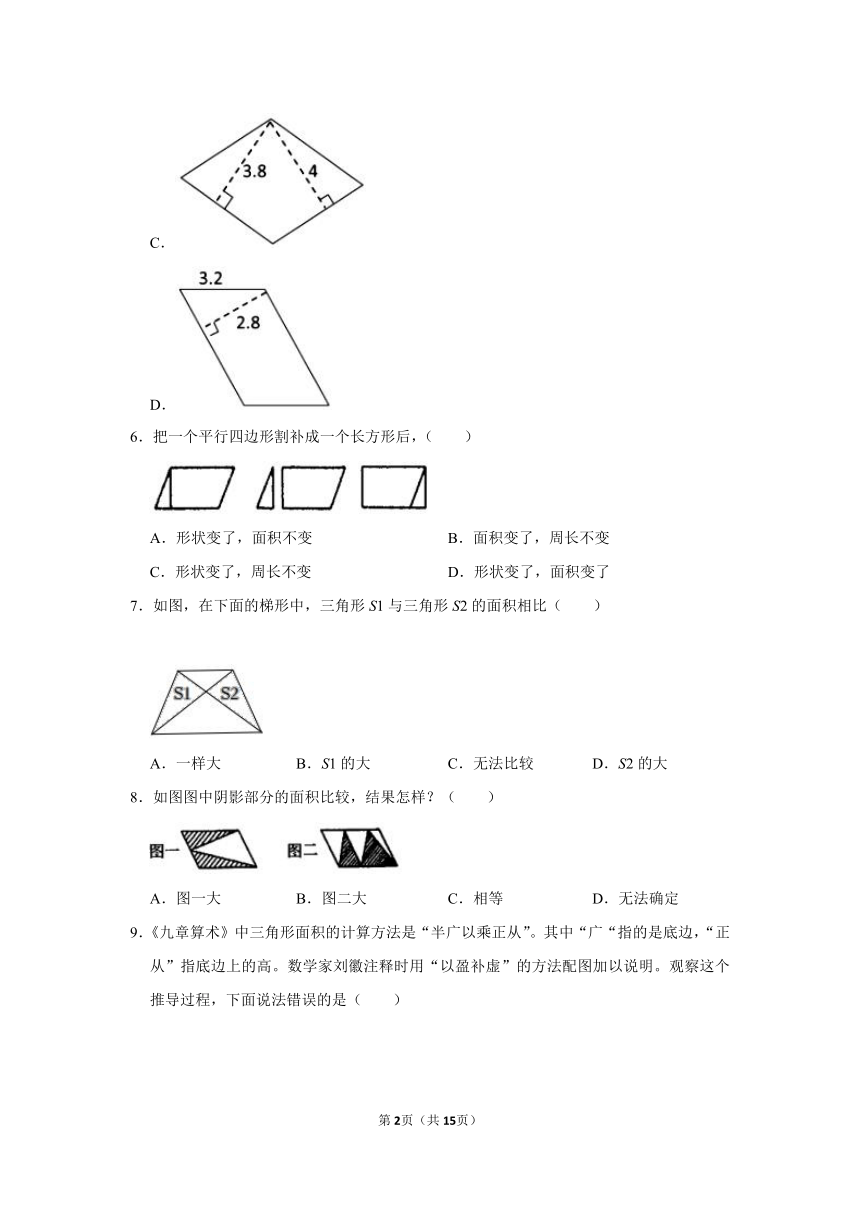
5.下列平行四边形中,利用已知信息能直接求出面积的是( )
A.
B.
C.
D.
6.把一个平行四边形割补成一个长方形后,( )
A.形状变了,面积不变 B.面积变了,周长不变
C.形状变了,周长不变 D.形状变了,面积变了
7.如图,在下面的梯形中,三角形S1与三角形S2的面积相比( )
A.一样大 B.S1的大 C.无法比较 D.S2的大
8.如图图中阴影部分的面积比较,结果怎样?( )
A.图一大 B.图二大 C.相等 D.无法确定
9.《九章算术》中三角形面积的计算方法是“半广以乘正从”。其中“广“指的是底边,“正从”指底边上的高。数学家刘徽注释时用“以盈补虚”的方法配图加以说明。观察这个推导过程,下面说法错误的是( )
A.拼成的平行四边形与三角形的高相等
B.平行四边形的底是三角形底边的一半
C.平行四边形的面积比三角形的面积小
D.三角形的面积=(底÷2)×高
二.填空题(共6小题)
10.一个三角形的底是1.2m,对应的高是3.5m,它的面积是 m2。与它等底等高的平行四边形的面积是 m2。
11.在如图的梯形中剪去一个最大的三角形,剩下的面积是 cm2。
12.一堆水管,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水管共有 根。
13.一个梯形的上底增加2厘米后就变成了一个边长为6厘米的正方形,这个梯形的面积是 平方厘米。
14.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是6厘米,则平行四边形的底是 厘米;如果平行四边形的底是10厘米,则三角形的底是 厘米。
15.如图,平行四边形两条底边分别长6分米、4分米,其中6分米底边上的高为3.5分米,那么4分米底边上的高为 分米。
三.操作题(共1小题)
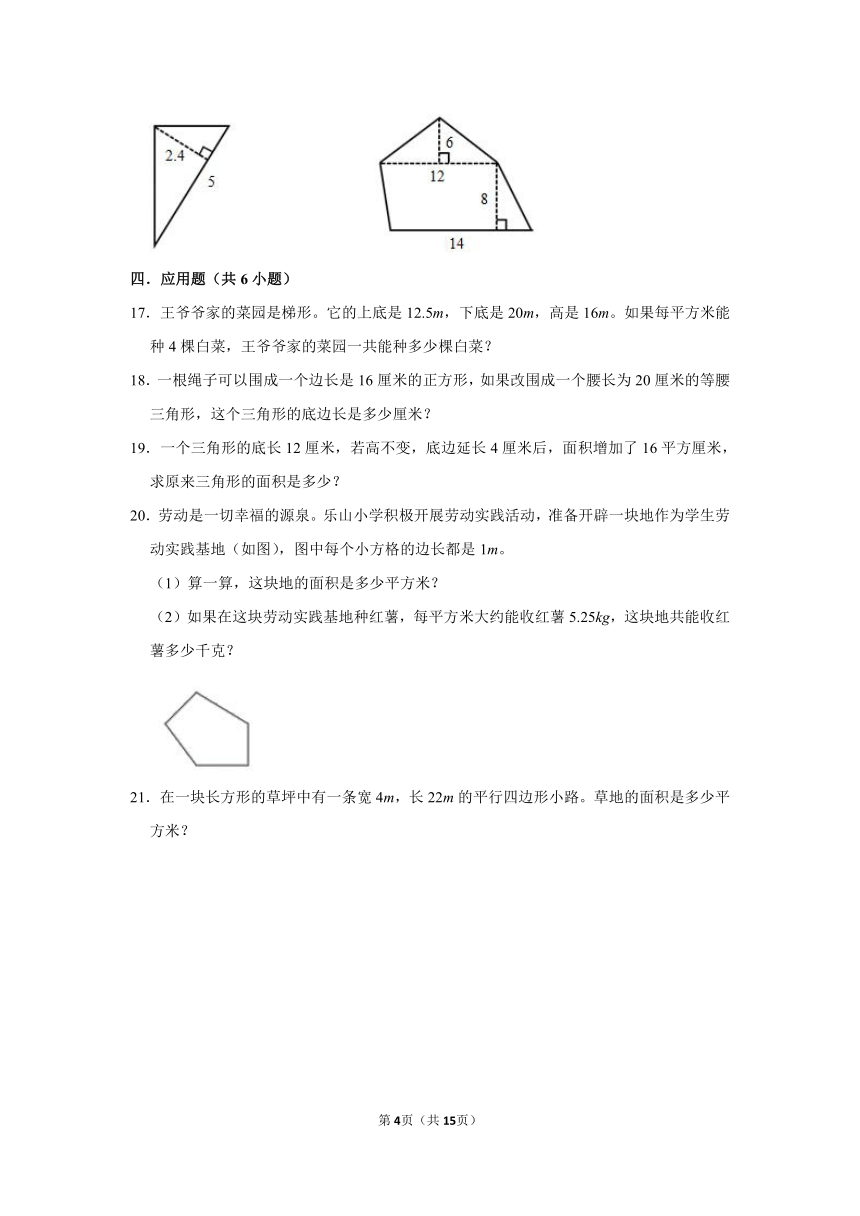
16.求下面各图形的面积(单位:dm)。
四.应用题(共6小题)
17.王爷爷家的菜园是梯形。它的上底是12.5m,下底是20m,高是16m。如果每平方米能种4棵白菜,王爷爷家的菜园一共能种多少棵白菜?
18.一根绳子可以围成一个边长是16厘米的正方形,如果改围成一个腰长为20厘米的等腰三角形,这个三角形的底边长是多少厘米?
19.一个三角形的底长12厘米,若高不变,底边延长4厘米后,面积增加了16平方厘米,求原来三角形的面积是多少?
20.劳动是一切幸福的源泉。乐山小学积极开展劳动实践活动,准备开辟一块地作为学生劳动实践基地(如图),图中每个小方格的边长都是1m。
(1)算一算,这块地的面积是多少平方米?
(2)如果在这块劳动实践基地种红薯,每平方米大约能收红薯5.25kg,这块地共能收红薯多少千克?
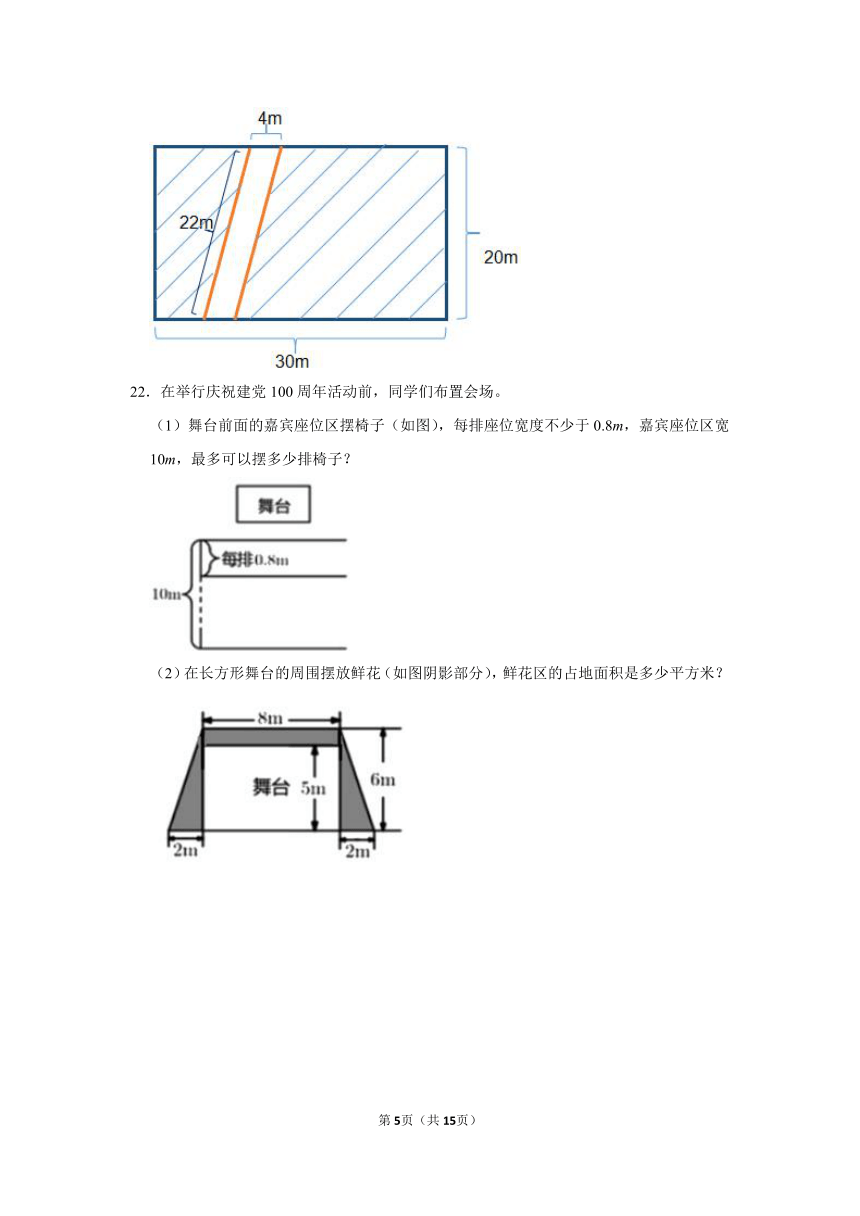
21.在一块长方形的草坪中有一条宽4m,长22m的平行四边形小路。草地的面积是多少平方米?
22.在举行庆祝建党100周年活动前,同学们布置会场。
(1)舞台前面的嘉宾座位区摆椅子(如图),每排座位宽度不少于0.8m,嘉宾座位区宽10m,最多可以摆多少排椅子?
(2)在长方形舞台的周围摆放鲜花(如图阴影部分),鲜花区的占地面积是多少平方米?
2022-2023学年上学期小学数学人教新版五年级同步经典题精练之多边形的面积综合题
参考答案与试题解析
一.选择题(共9小题)
1.如果把一个平行四边形活动框架拉成一个长方形,那么( )
A.周长和面积都不变 B.周长不变,面积变大
C.周长变大,面积不变 D.周长不变,面积变小
【解答】解:把一个平行四边形活动框架拉成一个长方形,那么现在的长方形与原来的平行四边形相比,周长不变,面积变大。
故选:B。
2.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是4cm,三角形的高是( )
A.2cm B.4cm C.8cm D.12cm
【解答】解:4×2=8(厘米)
答:三角形的高是8厘米。
故选:C。
3.有一堆钢管,最上层摆6根,最下层摆10根,每一层比上一层多1根,这堆钢管共有( )根。
A.40 B.50 C.60 D.80
【解答】解:(6+10)×(10﹣6+1)÷2
=16×5÷2
=80÷2
=40(根)
答:这堆钢管共有40根。
故选:A。
4.如图,平行线间三个阴影图形的面积关系是( )(单位:cm)
A.平行四边形的面积最大 B.梯形的面积最大
C.面积都相等
【解答】解:设它们的高为h厘米,
平行四边形的面积是4h(平方厘米);
三角形的面积是8h÷2=4h(平方厘米);
梯形的面积是(2+6)h÷2=4h(平方厘米);
所以,它们的面积相等。
故选:C。
5.下列平行四边形中,利用已知信息能直接求出面积的是( )
A.
B.
C.
D.
【解答】解:,面积=2×3.2=6.4;
,少高,不能求面积;
,少底,不能求面积;
少对应的底,不能求面积。
故选:A。
6.把一个平行四边形割补成一个长方形后,( )
A.形状变了,面积不变 B.面积变了,周长不变
C.形状变了,周长不变 D.形状变了,面积变了
【解答】解:把一个平行四边形割补成一个长方形后,形状变了,周长变小,面积不变。
故选:A。
7.如图,在下面的梯形中,三角形S1与三角形S2的面积相比( )
A.一样大 B.S1的大 C.无法比较 D.S2的大
【解答】解:
三角形ABC和三角形BCD等底等高,所以S1+S3=S2+S3。
所以S1=S2。
故选:A。
8.如图图中阴影部分的面积比较,结果怎样?( )
A.图一大 B.图二大 C.相等 D.无法确定
【解答】解:甲图阴影部分的面积是平行四边形面积的一半,乙图形中阴影部分的面积是平行四边形的面积一半,所以甲、乙图中阴影部分的面积相等。
故选:C。
9.《九章算术》中三角形面积的计算方法是“半广以乘正从”。其中“广“指的是底边,“正从”指底边上的高。数学家刘徽注释时用“以盈补虚”的方法配图加以说明。观察这个推导过程,下面说法错误的是( )
A.拼成的平行四边形与三角形的高相等
B.平行四边形的底是三角形底边的一半
C.平行四边形的面积比三角形的面积小
D.三角形的面积=(底÷2)×高
【解答】解:如上图:
A、拼成的平行四边形与三角形的高相等。此说法正确。
B、平行四边形的底是三角形底边的一半。此说法正确。
C、平行四边形的面积比三角形的面积小。此说法错误。
D、三角形的面积=(底÷2)×高。此说法正确。
故选:C。
二.填空题(共6小题)
10.一个三角形的底是1.2m,对应的高是3.5m,它的面积是 2.1 m2。与它等底等高的平行四边形的面积是 4.2 m2。
【解答】解:3.5×1.2÷2
=3.5×0.6
=2.1(m2)
2.1×2=4.2(m2)
答:三角形的面积是2.1m2,与它等底等高的平行四边形的面积是4.2m2。
故答案为:2.1,4.2。
11.在如图的梯形中剪去一个最大的三角形,剩下的面积是 1.44 cm2。
【解答】解:3.6×1.8÷2=3.24(平方厘米)
(3.6+1.6)×1.8÷2=4.68(平方厘米)
4.68﹣3.24=1.44(平方厘米)
答:剩下的面积是1.44平方厘米。
故答案为:1.44。
12.一堆水管,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水管共有 75 根。
【解答】解:(3+12)×10÷2
=15×10÷2
=75(根)
答:这堆水管共有75根。
故答案为:75。
13.一个梯形的上底增加2厘米后就变成了一个边长为6厘米的正方形,这个梯形的面积是 30 平方厘米。
【解答】解:6﹣2=4(厘米)
(4+6)×6÷2
=10×6÷2
=30(平方厘米)
答:这个梯形的面积是30平方厘米。
故答案为:30。
14.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是6厘米,则平行四边形的底是 3 厘米;如果平行四边形的底是10厘米,则三角形的底是 20 厘米。
【解答】解:6÷2=3(厘米)
10×2=20(厘米)
答:如果三角形的底是6厘米,则平行四边形的底是3厘米;如果平行四边形的底是10厘米,则三角形的底是20厘米。
故答案为:3,20。
15.如图,平行四边形两条底边分别长6分米、4分米,其中6分米底边上的高为3.5分米,那么4分米底边上的高为 5.25 分米。
【解答】解:6×3.5÷4
=21÷4
=5.25(分米)
答:4分米底边上的高是5.25分米。
故答案为:5.25。
三.操作题(共1小题)
16.求下面各图形的面积(单位:dm)。
【解答】解:(1)5×2.4÷2
=5×1.2
=6(平方分米)
答:三角形的面积是6平方分米。
(2)12×6÷2+(12+14)×8÷2
=36+104
=140(平方分米)
答:图形的面积是140平方分米。
四.应用题(共6小题)
17.王爷爷家的菜园是梯形。它的上底是12.5m,下底是20m,高是16m。如果每平方米能种4棵白菜,王爷爷家的菜园一共能种多少棵白菜?
【解答】解:(12.5+20)×16÷2×4
=260×4
=1040(棵)
答:王爷爷家的菜园一共能种1040棵白菜。
18.一根绳子可以围成一个边长是16厘米的正方形,如果改围成一个腰长为20厘米的等腰三角形,这个三角形的底边长是多少厘米?
【解答】解:16×4﹣20×2
=64﹣40
=24(厘米)
答:这个三角形的底边长24厘米。
19.一个三角形的底长12厘米,若高不变,底边延长4厘米后,面积增加了16平方厘米,求原来三角形的面积是多少?
【解答】解:16
=16×2÷4
=32÷4
=8(厘米)
×12×8=48(平方厘米)
答:原来三角形的面积是48平方厘米。
20.劳动是一切幸福的源泉。乐山小学积极开展劳动实践活动,准备开辟一块地作为学生劳动实践基地(如图),图中每个小方格的边长都是1m。
(1)算一算,这块地的面积是多少平方米?
(2)如果在这块劳动实践基地种红薯,每平方米大约能收红薯5.25kg,这块地共能收红薯多少千克?
【解答】解:(1)如图:
8×3÷2
=24÷2
=12(m )
(8+5)×4÷2
=52÷2
=26(m )
12+26=38(m )
答:这块地的面积是38平方米。
(2)5.25×38=199.5(千克)
答:这块地共能收红薯199.5千克。
21.在一块长方形的草坪中有一条宽4m,长22m的平行四边形小路。草地的面积是多少平方米?
【解答】解:30×20﹣4×20
=600﹣80
=520(平方米)
答:草地的面积是520平方米。
22.在举行庆祝建党100周年活动前,同学们布置会场。
(1)舞台前面的嘉宾座位区摆椅子(如图),每排座位宽度不少于0.8m,嘉宾座位区宽10m,最多可以摆多少排椅子?
(2)在长方形舞台的周围摆放鲜花(如图阴影部分),鲜花区的占地面积是多少平方米?
【解答】解:(1)10÷0.8≈12(排)
答:最多可以摆12排椅子。
(2)6×2+8×(6﹣5)
=12+8×1
=12+8
=20(平方米)
答:鲜花区的占地面积是20平方米。
第2页(共2页)
一.选择题(共9小题)
1.如果把一个平行四边形活动框架拉成一个长方形,那么( )
A.周长和面积都不变 B.周长不变,面积变大
C.周长变大,面积不变 D.周长不变,面积变小
2.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是4cm,三角形的高是( )
A.2cm B.4cm C.8cm D.12cm
3.有一堆钢管,最上层摆6根,最下层摆10根,每一层比上一层多1根,这堆钢管共有( )根。
A.40 B.50 C.60 D.80
4.如图,平行线间三个阴影图形的面积关系是( )(单位:cm)
A.平行四边形的面积最大 B.梯形的面积最大
C.面积都相等
5.下列平行四边形中,利用已知信息能直接求出面积的是( )
A.
B.
C.
D.
6.把一个平行四边形割补成一个长方形后,( )
A.形状变了,面积不变 B.面积变了,周长不变
C.形状变了,周长不变 D.形状变了,面积变了
7.如图,在下面的梯形中,三角形S1与三角形S2的面积相比( )
A.一样大 B.S1的大 C.无法比较 D.S2的大
8.如图图中阴影部分的面积比较,结果怎样?( )
A.图一大 B.图二大 C.相等 D.无法确定
9.《九章算术》中三角形面积的计算方法是“半广以乘正从”。其中“广“指的是底边,“正从”指底边上的高。数学家刘徽注释时用“以盈补虚”的方法配图加以说明。观察这个推导过程,下面说法错误的是( )
A.拼成的平行四边形与三角形的高相等
B.平行四边形的底是三角形底边的一半
C.平行四边形的面积比三角形的面积小
D.三角形的面积=(底÷2)×高
二.填空题(共6小题)
10.一个三角形的底是1.2m,对应的高是3.5m,它的面积是 m2。与它等底等高的平行四边形的面积是 m2。
11.在如图的梯形中剪去一个最大的三角形,剩下的面积是 cm2。
12.一堆水管,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水管共有 根。
13.一个梯形的上底增加2厘米后就变成了一个边长为6厘米的正方形,这个梯形的面积是 平方厘米。
14.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是6厘米,则平行四边形的底是 厘米;如果平行四边形的底是10厘米,则三角形的底是 厘米。
15.如图,平行四边形两条底边分别长6分米、4分米,其中6分米底边上的高为3.5分米,那么4分米底边上的高为 分米。
三.操作题(共1小题)
16.求下面各图形的面积(单位:dm)。
四.应用题(共6小题)
17.王爷爷家的菜园是梯形。它的上底是12.5m,下底是20m,高是16m。如果每平方米能种4棵白菜,王爷爷家的菜园一共能种多少棵白菜?
18.一根绳子可以围成一个边长是16厘米的正方形,如果改围成一个腰长为20厘米的等腰三角形,这个三角形的底边长是多少厘米?
19.一个三角形的底长12厘米,若高不变,底边延长4厘米后,面积增加了16平方厘米,求原来三角形的面积是多少?
20.劳动是一切幸福的源泉。乐山小学积极开展劳动实践活动,准备开辟一块地作为学生劳动实践基地(如图),图中每个小方格的边长都是1m。
(1)算一算,这块地的面积是多少平方米?
(2)如果在这块劳动实践基地种红薯,每平方米大约能收红薯5.25kg,这块地共能收红薯多少千克?
21.在一块长方形的草坪中有一条宽4m,长22m的平行四边形小路。草地的面积是多少平方米?
22.在举行庆祝建党100周年活动前,同学们布置会场。
(1)舞台前面的嘉宾座位区摆椅子(如图),每排座位宽度不少于0.8m,嘉宾座位区宽10m,最多可以摆多少排椅子?
(2)在长方形舞台的周围摆放鲜花(如图阴影部分),鲜花区的占地面积是多少平方米?
2022-2023学年上学期小学数学人教新版五年级同步经典题精练之多边形的面积综合题
参考答案与试题解析
一.选择题(共9小题)
1.如果把一个平行四边形活动框架拉成一个长方形,那么( )
A.周长和面积都不变 B.周长不变,面积变大
C.周长变大,面积不变 D.周长不变,面积变小
【解答】解:把一个平行四边形活动框架拉成一个长方形,那么现在的长方形与原来的平行四边形相比,周长不变,面积变大。
故选:B。
2.一个三角形与一个平行四边形的底相等,面积也相等,平行四边形的高是4cm,三角形的高是( )
A.2cm B.4cm C.8cm D.12cm
【解答】解:4×2=8(厘米)
答:三角形的高是8厘米。
故选:C。
3.有一堆钢管,最上层摆6根,最下层摆10根,每一层比上一层多1根,这堆钢管共有( )根。
A.40 B.50 C.60 D.80
【解答】解:(6+10)×(10﹣6+1)÷2
=16×5÷2
=80÷2
=40(根)
答:这堆钢管共有40根。
故选:A。
4.如图,平行线间三个阴影图形的面积关系是( )(单位:cm)
A.平行四边形的面积最大 B.梯形的面积最大
C.面积都相等
【解答】解:设它们的高为h厘米,
平行四边形的面积是4h(平方厘米);
三角形的面积是8h÷2=4h(平方厘米);
梯形的面积是(2+6)h÷2=4h(平方厘米);
所以,它们的面积相等。
故选:C。
5.下列平行四边形中,利用已知信息能直接求出面积的是( )
A.
B.
C.
D.
【解答】解:,面积=2×3.2=6.4;
,少高,不能求面积;
,少底,不能求面积;
少对应的底,不能求面积。
故选:A。
6.把一个平行四边形割补成一个长方形后,( )
A.形状变了,面积不变 B.面积变了,周长不变
C.形状变了,周长不变 D.形状变了,面积变了
【解答】解:把一个平行四边形割补成一个长方形后,形状变了,周长变小,面积不变。
故选:A。
7.如图,在下面的梯形中,三角形S1与三角形S2的面积相比( )
A.一样大 B.S1的大 C.无法比较 D.S2的大
【解答】解:
三角形ABC和三角形BCD等底等高,所以S1+S3=S2+S3。
所以S1=S2。
故选:A。
8.如图图中阴影部分的面积比较,结果怎样?( )
A.图一大 B.图二大 C.相等 D.无法确定
【解答】解:甲图阴影部分的面积是平行四边形面积的一半,乙图形中阴影部分的面积是平行四边形的面积一半,所以甲、乙图中阴影部分的面积相等。
故选:C。
9.《九章算术》中三角形面积的计算方法是“半广以乘正从”。其中“广“指的是底边,“正从”指底边上的高。数学家刘徽注释时用“以盈补虚”的方法配图加以说明。观察这个推导过程,下面说法错误的是( )
A.拼成的平行四边形与三角形的高相等
B.平行四边形的底是三角形底边的一半
C.平行四边形的面积比三角形的面积小
D.三角形的面积=(底÷2)×高
【解答】解:如上图:
A、拼成的平行四边形与三角形的高相等。此说法正确。
B、平行四边形的底是三角形底边的一半。此说法正确。
C、平行四边形的面积比三角形的面积小。此说法错误。
D、三角形的面积=(底÷2)×高。此说法正确。
故选:C。
二.填空题(共6小题)
10.一个三角形的底是1.2m,对应的高是3.5m,它的面积是 2.1 m2。与它等底等高的平行四边形的面积是 4.2 m2。
【解答】解:3.5×1.2÷2
=3.5×0.6
=2.1(m2)
2.1×2=4.2(m2)
答:三角形的面积是2.1m2,与它等底等高的平行四边形的面积是4.2m2。
故答案为:2.1,4.2。
11.在如图的梯形中剪去一个最大的三角形,剩下的面积是 1.44 cm2。
【解答】解:3.6×1.8÷2=3.24(平方厘米)
(3.6+1.6)×1.8÷2=4.68(平方厘米)
4.68﹣3.24=1.44(平方厘米)
答:剩下的面积是1.44平方厘米。
故答案为:1.44。
12.一堆水管,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水管共有 75 根。
【解答】解:(3+12)×10÷2
=15×10÷2
=75(根)
答:这堆水管共有75根。
故答案为:75。
13.一个梯形的上底增加2厘米后就变成了一个边长为6厘米的正方形,这个梯形的面积是 30 平方厘米。
【解答】解:6﹣2=4(厘米)
(4+6)×6÷2
=10×6÷2
=30(平方厘米)
答:这个梯形的面积是30平方厘米。
故答案为:30。
14.一个三角形和一个平行四边形的面积相等,高也相等,如果三角形的底是6厘米,则平行四边形的底是 3 厘米;如果平行四边形的底是10厘米,则三角形的底是 20 厘米。
【解答】解:6÷2=3(厘米)
10×2=20(厘米)
答:如果三角形的底是6厘米,则平行四边形的底是3厘米;如果平行四边形的底是10厘米,则三角形的底是20厘米。
故答案为:3,20。
15.如图,平行四边形两条底边分别长6分米、4分米,其中6分米底边上的高为3.5分米,那么4分米底边上的高为 5.25 分米。
【解答】解:6×3.5÷4
=21÷4
=5.25(分米)
答:4分米底边上的高是5.25分米。
故答案为:5.25。
三.操作题(共1小题)
16.求下面各图形的面积(单位:dm)。
【解答】解:(1)5×2.4÷2
=5×1.2
=6(平方分米)
答:三角形的面积是6平方分米。
(2)12×6÷2+(12+14)×8÷2
=36+104
=140(平方分米)
答:图形的面积是140平方分米。
四.应用题(共6小题)
17.王爷爷家的菜园是梯形。它的上底是12.5m,下底是20m,高是16m。如果每平方米能种4棵白菜,王爷爷家的菜园一共能种多少棵白菜?
【解答】解:(12.5+20)×16÷2×4
=260×4
=1040(棵)
答:王爷爷家的菜园一共能种1040棵白菜。
18.一根绳子可以围成一个边长是16厘米的正方形,如果改围成一个腰长为20厘米的等腰三角形,这个三角形的底边长是多少厘米?
【解答】解:16×4﹣20×2
=64﹣40
=24(厘米)
答:这个三角形的底边长24厘米。
19.一个三角形的底长12厘米,若高不变,底边延长4厘米后,面积增加了16平方厘米,求原来三角形的面积是多少?
【解答】解:16
=16×2÷4
=32÷4
=8(厘米)
×12×8=48(平方厘米)
答:原来三角形的面积是48平方厘米。
20.劳动是一切幸福的源泉。乐山小学积极开展劳动实践活动,准备开辟一块地作为学生劳动实践基地(如图),图中每个小方格的边长都是1m。
(1)算一算,这块地的面积是多少平方米?
(2)如果在这块劳动实践基地种红薯,每平方米大约能收红薯5.25kg,这块地共能收红薯多少千克?
【解答】解:(1)如图:
8×3÷2
=24÷2
=12(m )
(8+5)×4÷2
=52÷2
=26(m )
12+26=38(m )
答:这块地的面积是38平方米。
(2)5.25×38=199.5(千克)
答:这块地共能收红薯199.5千克。
21.在一块长方形的草坪中有一条宽4m,长22m的平行四边形小路。草地的面积是多少平方米?
【解答】解:30×20﹣4×20
=600﹣80
=520(平方米)
答:草地的面积是520平方米。
22.在举行庆祝建党100周年活动前,同学们布置会场。
(1)舞台前面的嘉宾座位区摆椅子(如图),每排座位宽度不少于0.8m,嘉宾座位区宽10m,最多可以摆多少排椅子?
(2)在长方形舞台的周围摆放鲜花(如图阴影部分),鲜花区的占地面积是多少平方米?
【解答】解:(1)10÷0.8≈12(排)
答:最多可以摆12排椅子。
(2)6×2+8×(6﹣5)
=12+8×1
=12+8
=20(平方米)
答:鲜花区的占地面积是20平方米。
第2页(共2页)
