13.3.2 等边三角形(2)课件(19张PPT)
文档属性
| 名称 | 13.3.2 等边三角形(2)课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1023.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-07 20:17:00 | ||
图片预览




文档简介
(共19张PPT)
13.3.2等边三角形(2)
人教版八年级上册
教学目标
(1)运用等边三角形能推导出30°角的直角三角形的性质.
(2)能运用30°角的直角三角形的性质解决相关问题.
新知导入
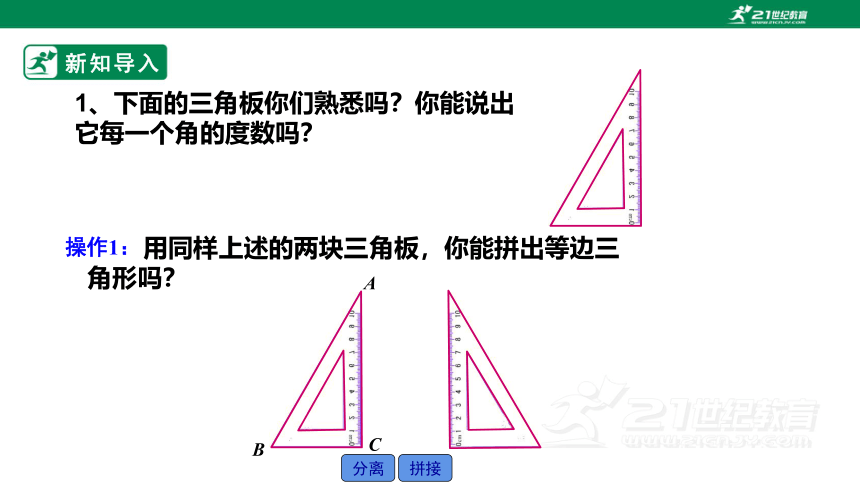
1、下面的三角板你们熟悉吗?你能说出它每一个角的度数吗?
用同样上述的两块三角板,你能拼出等边三角形吗?
分离
拼接
A
C
B
操作1:
新知讲解
将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
操作2:
新知讲解
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,显然,△ADC与△ABC关于AC成轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
新知讲解
证明:
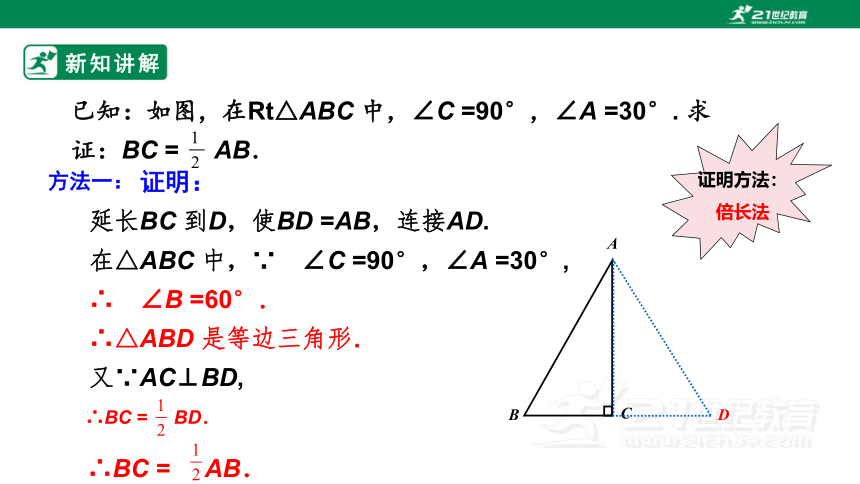
延长BC 到D,使BD =AB,连接AD.
在△ABC 中,∵ ∠C =90°,∠A =30°, ∴ ∠B =60°.
∴△ABD 是等边三角形.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
A
B
C
D
证明方法:倍长法
∴BC = AB.
∴BC = BD.
方法一:
新知讲解
E
A
B
C
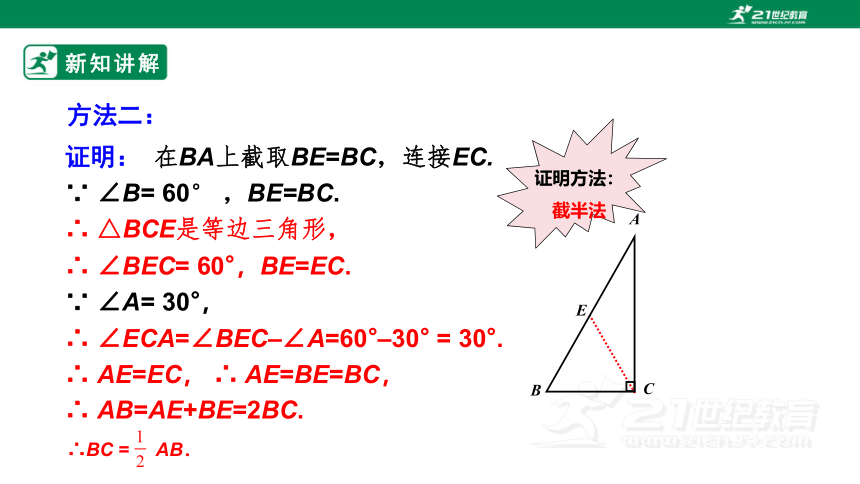
证明: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC–∠A=60°–30° = 30°.
∴ AE=EC, ∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴BC = AB.
证明方法:截半法
方法二:
新知讲解
符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
∴ BC = AB.
归纳总结
巩固练习
1、Rt△ABC 中,∠C =90°,∠B =2∠A,∠B 和∠A 各是多少度?边AB 与BC 之间有什么关系?
证明:∵∠B+∠A=180°- ∠C=90°,
∠B=2∠A,
∴∠B=60°,∠A=30°.
∴ AB=2BC.
【课本P81 练习】
巩固练习
2、如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户.如果∠C = 90°,∠B = 30°,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,并在图上画出来.
解:如图,作∠CAB 的平分线,交 BC 于点 D,过点 D 作 DE ⊥ AB,垂足为E. 则△ABC 就分成了三个大小、形状都相同的三角形,即△AED,△ACD和△BED.
【课本P83 15题】
例题讲解
例 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长.
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
巩固练习
证明:∵∠ACB=90°,CD⊥BA,∠A=30°,
∴∠ACD=60°,∠BCD=30°,∠CDB=∠CDA=90°.
∴BD= BC,BC= AB,
∴BD= AB.
3.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°.求证:BD= AB.
巩固练习
4.如图所示, 在△ABC中,BD是AC边上的中线,延长BD至E,使DE = BD,DB⊥BC于B,∠ABC = 120°, 求证: AB = 2BC.
证明:∵BD是AC的中线,∴AD=CD.
在△ADE和△CDB中,
AD = CD,
∠ADE =∠CDB,
DE = DB,
∴△ADE≌△CDB (SAS).
∴∠E = ∠CBD = 90°,AE = BC.
又∠ABC = 120°,∴∠ABE = 30°.
∴在Rt△ABE中,AB=2AE∴AB=2BC.
课堂总结
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
含30°角的直角三角形的性质
①分清30 °的角所在的直角边
②作辅助线,构造直角三角形
注意
前提条件:直角三角形中
证题方法
倍长法
截半法
拓展提高
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城绿化改造中,计划在一块如图所示的△ABC空地上种植草皮优化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
拓展提高
4.等腰三角形一腰上的高与腰长之比为1∶2,则等腰三角形的顶角为( )
A.30° B.60° C.150° D.30°或150°
D
3. Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4 cm C.8 cm D.16cm
C
拓展提高
5.如图,已知△ABC是等边三角形,D,E分别为BC,AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q,求证:BP=2PQ.
∴△ADC≌△BEA.
证明:∵△ABC为等边三角形,
∴ AC=BC=AB ,∠C=∠BAC=60°,
∵CD=AE,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.2等边三角形(2)
人教版八年级上册
教学目标
(1)运用等边三角形能推导出30°角的直角三角形的性质.
(2)能运用30°角的直角三角形的性质解决相关问题.
新知导入
1、下面的三角板你们熟悉吗?你能说出它每一个角的度数吗?
用同样上述的两块三角板,你能拼出等边三角形吗?
分离
拼接
A
C
B
操作1:
新知讲解
将一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
操作2:
新知讲解
性质:
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
D
如图,显然,△ADC与△ABC关于AC成轴对称图形,
因此AB=AD, ∠BAD=2×30°=60°,
从而△ABD是一个等边三角形.
再由AC⊥BD,
可得BC=CD= AB.
你还能用其他方法证明吗?
新知讲解
证明:
延长BC 到D,使BD =AB,连接AD.
在△ABC 中,∵ ∠C =90°,∠A =30°, ∴ ∠B =60°.
∴△ABD 是等边三角形.
又∵AC⊥BD,
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
A
B
C
D
证明方法:倍长法
∴BC = AB.
∴BC = BD.
方法一:
新知讲解
E
A
B
C
证明: 在BA上截取BE=BC,连接EC.
∵ ∠B= 60° ,BE=BC.
∴ △BCE是等边三角形,
∴ ∠BEC= 60°,BE=EC.
∵ ∠A= 30°,
∴ ∠ECA=∠BEC–∠A=60°–30° = 30°.
∴ AE=EC, ∴ AE=BE=BC,
∴ AB=AE+BE=2BC.
∴BC = AB.
证明方法:截半法
方法二:
新知讲解
符号语言:
∵ 在Rt△ABC 中,
∠C =90°,∠A =30°,
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
A
B
C
∴ BC = AB.
归纳总结
巩固练习
1、Rt△ABC 中,∠C =90°,∠B =2∠A,∠B 和∠A 各是多少度?边AB 与BC 之间有什么关系?
证明:∵∠B+∠A=180°- ∠C=90°,
∠B=2∠A,
∴∠B=60°,∠A=30°.
∴ AB=2BC.
【课本P81 练习】
巩固练习
2、如图,要把一块三角形的土地均匀分给甲、乙、丙三家农户.如果∠C = 90°,∠B = 30°,要使这三家农户所得土地的大小、形状都相同,请你试着分一分,并在图上画出来.
解:如图,作∠CAB 的平分线,交 BC 于点 D,过点 D 作 DE ⊥ AB,垂足为E. 则△ABC 就分成了三个大小、形状都相同的三角形,即△AED,△ACD和△BED.
【课本P83 15题】
例题讲解
例 如图是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC、DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC、DE 要多长.
A
B
C
D
E
解:∵ DE⊥AC,BC⊥AC,∠A =30°,
∴ BC = AB,DE = AD.
又 AD = AB,
∴ DE = AD =1.85(m) .
∴ BC =3.7(m).
答:立柱BC 的长是3.7 m,DE 的长是1.85 m.
巩固练习
证明:∵∠ACB=90°,CD⊥BA,∠A=30°,
∴∠ACD=60°,∠BCD=30°,∠CDB=∠CDA=90°.
∴BD= BC,BC= AB,
∴BD= AB.
3.如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°.求证:BD= AB.
巩固练习
4.如图所示, 在△ABC中,BD是AC边上的中线,延长BD至E,使DE = BD,DB⊥BC于B,∠ABC = 120°, 求证: AB = 2BC.
证明:∵BD是AC的中线,∴AD=CD.
在△ADE和△CDB中,
AD = CD,
∠ADE =∠CDB,
DE = DB,
∴△ADE≌△CDB (SAS).
∴∠E = ∠CBD = 90°,AE = BC.
又∠ABC = 120°,∴∠ABE = 30°.
∴在Rt△ABE中,AB=2AE∴AB=2BC.
课堂总结
内容
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
使用要点
含30°角的直角三角形的性质
①分清30 °的角所在的直角边
②作辅助线,构造直角三角形
注意
前提条件:直角三角形中
证题方法
倍长法
截半法
拓展提高
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米
C.12米 D.15米
2.某市在旧城绿化改造中,计划在一块如图所示的△ABC空地上种植草皮优化环境,已知∠A=150°,这种草皮每平方米售价a元,则购买这种草皮至少需要( )
A.300a元 B.150a元
C.450a元 D.225a元
B
B
拓展提高
4.等腰三角形一腰上的高与腰长之比为1∶2,则等腰三角形的顶角为( )
A.30° B.60° C.150° D.30°或150°
D
3. Rt△ABC中,CD是斜边AB上的高,∠B=30°,AD=2cm,则AB的长度是( )
A.2cm B.4 cm C.8 cm D.16cm
C
拓展提高
5.如图,已知△ABC是等边三角形,D,E分别为BC,AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q,求证:BP=2PQ.
∴△ADC≌△BEA.
证明:∵△ABC为等边三角形,
∴ AC=BC=AB ,∠C=∠BAC=60°,
∵CD=AE,
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
