沪科版八年级数学上册第14章《全等三角形》小结评价(单元复习)
文档属性
| 名称 | 沪科版八年级数学上册第14章《全等三角形》小结评价(单元复习) |  | |
| 格式 | zip | ||
| 文件大小 | 97.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-11-01 13:51:57 | ||
图片预览



文档简介
课件15张PPT。沪科版八年级数学上册 第十四章 全等三角形小结 评价(1课时)1、全等三角形的概念:能完全重合的两个三角形叫做全等三角形。2、全等三角形的特征:全等三角形的对应边相等,对应角相等。3、全等三角形的识别:(1)一般三角形全等的识别:SSS,SAS,ASA,AAS(2)直角三角形全等的识别:除以上方法外,还有HLAAA—三角对应相等的两个三角形不一定全等
一、知识点复习:SSA—两边和其中一边的对角对应相等的两个三角形不一定全等
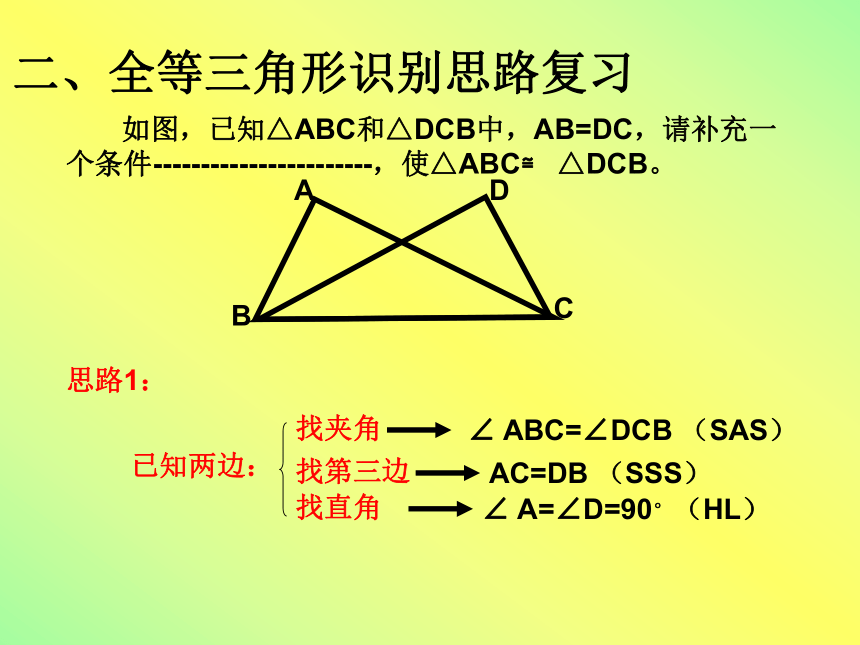
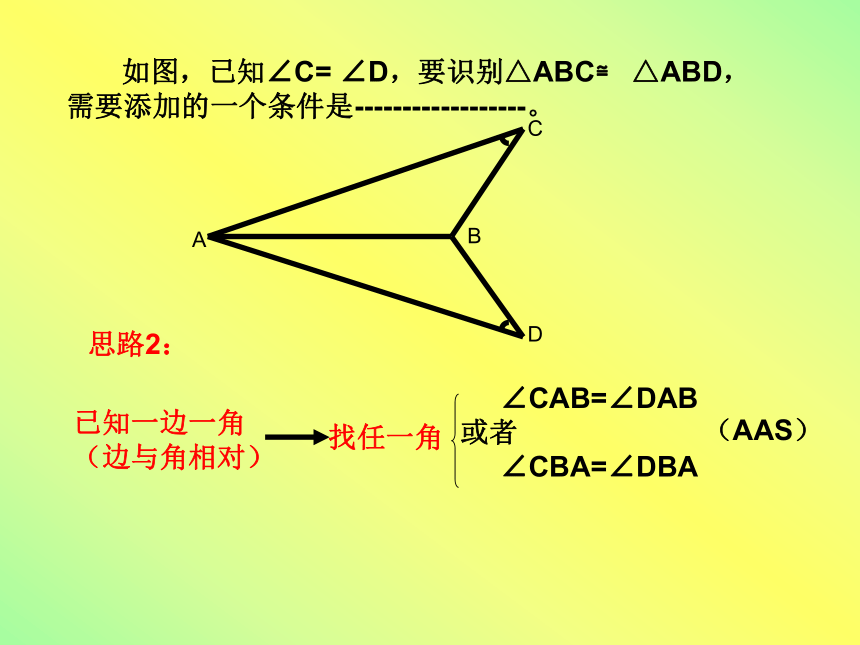
二、全等三角形识别思路复习 如图,已知△ABC和△DCB中,AB=DC,请补充一个条件-----------------------,使△ABC≌ △DCB。思路1:找夹角找第三边找直角已知两边:∠ ABC=∠DCB (SAS)AC=DB (SSS)∠ A=∠D=90°(HL) 如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是------------------。思路2:找任一角已知一边一角
(边与角相对)(AAS) ∠CAB=∠DAB
或者
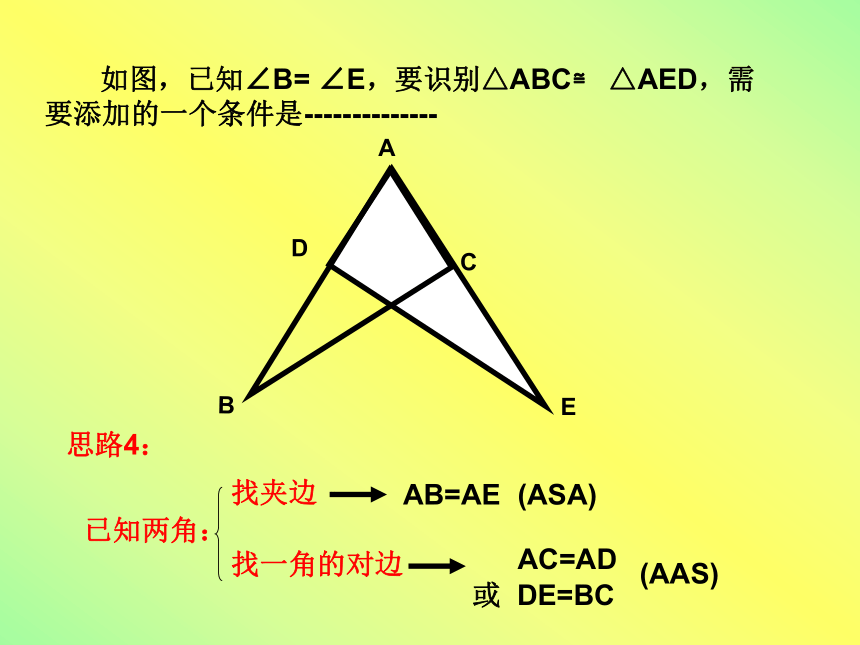
∠CBA=∠DBAACBD 如图,已知∠1= ∠2,要识别△ABC≌ △CDA,需要添加的一个条件是----------------- 思路3:已知一边一角(边与角相邻):ABCD21找夹这个角的另一边找夹这条边的另一角找边的对角AD=CB∠ACD=∠CAB∠D=∠B(SAS)(ASA)(AAS) 如图,已知∠B= ∠E,要识别△ABC≌ △AED,需要添加的一个条件是--------------思路4:已知两角:找夹边找一角的对边AB=AEAC=AD或 DE=BC(ASA)(AAS)小
试
锋
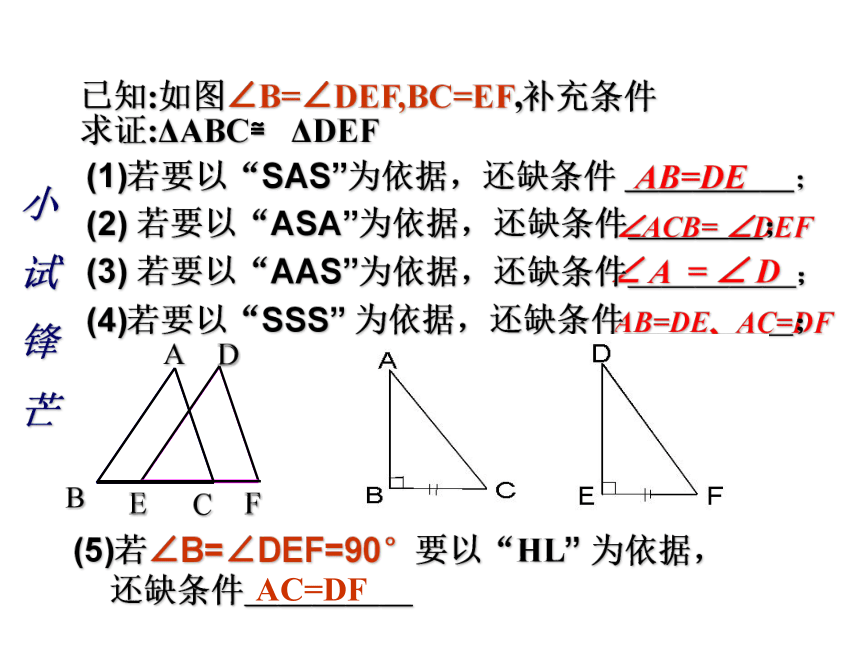
芒已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌ ΔDEF∠ACB= ∠DEFAB=DEAB=DE、AC=DF∠ A = ∠ D(1)若要以“SAS”为依据,还缺条件 _____;(2) 若要以“ASA”为依据,还缺条件____; (4)若要以“SSS” 为依据,还缺条件_____;(3) 若要以“AAS”为依据,还缺条件_____; (5)若∠B=∠DEF=90°要以“HL” 为依据,
还缺条件_____AC=DF三、例题选析例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B. ∠AEB=∠ADC
C.BE=CD D.AB=ACB例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对 D∠BPC△APC和△BPCPA=PB(已知)PC=PC(公共边)△APC △BPCSAS全等三角形对应角相等方法点拨:1、证角(或线段)相等转化为证角(或线段)所在的三角形全等;2、四边形问题转化为三角形问题来解决。3、两个三角形全等,通常需要3个条件,其中至少要有1组边对应相等。 例4、已知:如图,AD与BE交于F,AF=BF, ∠1=∠2.
求证:AC=BC
ABDCEF12证明:∵ ∠AFE=∠BFD (对顶角相等) 又∵ ∠1=∠2 (已知) ∴∠AFE+∠1=∠BFD+∠2 (等式性质) 即 ∠AFC=∠BFC 创造全等条件在△AFC与△BFC中 AF=BF (已知) ∠AFC=∠BFC (已证) CF=CF (公共边) 列齐全等条件∴ △AFC≌△BFC (SAS) 得出结论
∴ AC=BC △AFC△BFC例5、如图,已知AB=CD,AD=CB,求证:∠B=∠D证明:连结AC,AB=CD(已知)AC=CA(公共边)BC=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?答:∠ABC=∠ADC,AB∥CD,AD∥BC在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。例6、已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP小结:找夹角(SAS)找第三边(SSS)找直角(HL)已知两边找任一角(AAS)已知一边一角 (边与角相邻)找夹这个角的另一边(SAS)找夹这条边的另一角(ASA)找边的对角(AAS)已知两角找夹边(ASA)找一边的对角(AAS)1、全等三角形识别思路:3、三角形全等是证明线段相等,角相等的重要途径。(边与角相对)2、经过平移、翻折、旋转等变换得到的三角形和原三角形全等。注意:1、“分别对应相等”是关键;
2、已知两边及其中一边的对角分别对应相等的两个三角形不一定全等。练习求:∠DBE的度数.
?
?
?
A
C
B
D
1 如图,A、B、C三点在一条直线上,DA⊥AC,EC⊥AC,AB=CE,AD=CB.
EB
C
E
A
2 如图,A、B、C三点在一条直线上,AD=AE,AC平分∠DAE,图中有多少对全等三角形?证明你的结论.
D
一、知识点复习:SSA—两边和其中一边的对角对应相等的两个三角形不一定全等
二、全等三角形识别思路复习 如图,已知△ABC和△DCB中,AB=DC,请补充一个条件-----------------------,使△ABC≌ △DCB。思路1:找夹角找第三边找直角已知两边:∠ ABC=∠DCB (SAS)AC=DB (SSS)∠ A=∠D=90°(HL) 如图,已知∠C= ∠D,要识别△ABC≌ △ABD,需要添加的一个条件是------------------。思路2:找任一角已知一边一角
(边与角相对)(AAS) ∠CAB=∠DAB
或者
∠CBA=∠DBAACBD 如图,已知∠1= ∠2,要识别△ABC≌ △CDA,需要添加的一个条件是----------------- 思路3:已知一边一角(边与角相邻):ABCD21找夹这个角的另一边找夹这条边的另一角找边的对角AD=CB∠ACD=∠CAB∠D=∠B(SAS)(ASA)(AAS) 如图,已知∠B= ∠E,要识别△ABC≌ △AED,需要添加的一个条件是--------------思路4:已知两角:找夹边找一角的对边AB=AEAC=AD或 DE=BC(ASA)(AAS)小
试
锋
芒已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌ ΔDEF∠ACB= ∠DEFAB=DEAB=DE、AC=DF∠ A = ∠ D(1)若要以“SAS”为依据,还缺条件 _____;(2) 若要以“ASA”为依据,还缺条件____; (4)若要以“SSS” 为依据,还缺条件_____;(3) 若要以“AAS”为依据,还缺条件_____; (5)若∠B=∠DEF=90°要以“HL” 为依据,
还缺条件_____AC=DF三、例题选析例1:如图,D在AB上,E在AC上,且∠B =∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A.AD=AE B. ∠AEB=∠ADC
C.BE=CD D.AB=ACB例2:已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对 D∠BPC△APC和△BPCPA=PB(已知)PC=PC(公共边)△APC △BPCSAS全等三角形对应角相等方法点拨:1、证角(或线段)相等转化为证角(或线段)所在的三角形全等;2、四边形问题转化为三角形问题来解决。3、两个三角形全等,通常需要3个条件,其中至少要有1组边对应相等。 例4、已知:如图,AD与BE交于F,AF=BF, ∠1=∠2.
求证:AC=BC
ABDCEF12证明:∵ ∠AFE=∠BFD (对顶角相等) 又∵ ∠1=∠2 (已知) ∴∠AFE+∠1=∠BFD+∠2 (等式性质) 即 ∠AFC=∠BFC 创造全等条件在△AFC与△BFC中 AF=BF (已知) ∠AFC=∠BFC (已证) CF=CF (公共边) 列齐全等条件∴ △AFC≌△BFC (SAS) 得出结论
∴ AC=BC △AFC△BFC例5、如图,已知AB=CD,AD=CB,求证:∠B=∠D证明:连结AC,AB=CD(已知)AC=CA(公共边)BC=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?答:∠ABC=∠ADC,AB∥CD,AD∥BC在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。例6、已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DP
证明:在Rt?ABC和Rt?ABD中∴Rt?ABC≌Rt?ABD∴∠CAB=∠DAB∴?APC≌?APD(SAS)∴CP=DP小结:找夹角(SAS)找第三边(SSS)找直角(HL)已知两边找任一角(AAS)已知一边一角 (边与角相邻)找夹这个角的另一边(SAS)找夹这条边的另一角(ASA)找边的对角(AAS)已知两角找夹边(ASA)找一边的对角(AAS)1、全等三角形识别思路:3、三角形全等是证明线段相等,角相等的重要途径。(边与角相对)2、经过平移、翻折、旋转等变换得到的三角形和原三角形全等。注意:1、“分别对应相等”是关键;
2、已知两边及其中一边的对角分别对应相等的两个三角形不一定全等。练习求:∠DBE的度数.
?
?
?
A
C
B
D
1 如图,A、B、C三点在一条直线上,DA⊥AC,EC⊥AC,AB=CE,AD=CB.
EB
C
E
A
2 如图,A、B、C三点在一条直线上,AD=AE,AC平分∠DAE,图中有多少对全等三角形?证明你的结论.
D
