湘教版九年级数学下册 1.2 二次函数的图像与性质 练习(无答案)
文档属性
| 名称 | 湘教版九年级数学下册 1.2 二次函数的图像与性质 练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 00:00:00 | ||
图片预览


文档简介
二次函数的图像与性质
【知识梳理】
1. 二次函数的图像特征与a,b,c的关系
(1)a的符号与绝对值的大小<=>抛物线的开口方向与大小
(2)c的值就是图象与y轴交点的纵坐标
(3)对称轴与a,b的关系(简记口诀“左同右异”)
(4)的符号与抛物线与x轴交点的个数的关系
2. 图像的平移(简记为“上加下减、左加右减”)
3. 二次函数(a≠0)的性质
条件 图像 增减性 最值
a的符号 >0 =0 <0 对称轴为
a>0
a<0
4. 二次函数与一元二次方程的关系(判断依据:)
【基础巩固】
选择题( 每小题3 分,共30分 )
1、抛物线的顶点坐标是( )
(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
2、二次函数的最小值是( ).
2 B.1 C.-3 D.
3、在平面直角坐标系中,将二次函数的图象向上平移2个单位,所得图象的解析式为( )
A. B. C. D.
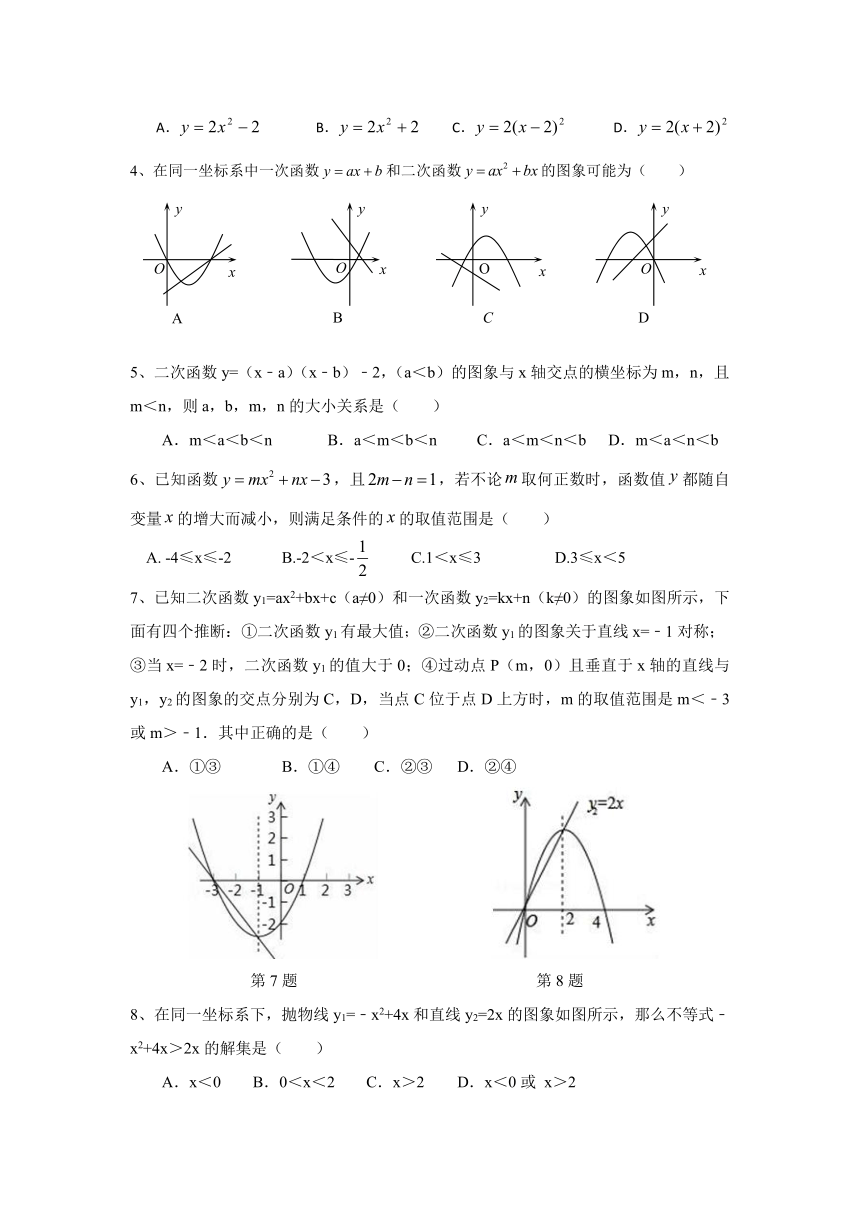
4、在同一坐标系中一次函数和二次函数的图象可能为( )
(
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
)
5、二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )
A.m<a<b<n B.a<m<b<n C.a<m<n<b D.m<a<n<b
6、已知函数,且,若不论取何正数时,函数值都随自变量的增大而减小,则满足条件的的取值范围是( )
A. -4≤x≤-2 B.-2<x≤- C.1<x≤3 D.3≤x<5
7、已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:①二次函数y1有最大值;②二次函数y1的图象关于直线x=﹣1对称;
③当x=﹣2时,二次函数y1的值大于0;④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.其中正确的是( )
A.①③ B.①④ C.②③ D.②④
第7题 第8题
8、在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式﹣x2+4x>2x的解集是( )
A.x<0 B.0<x<2 C.x>2 D.x<0或 x>2
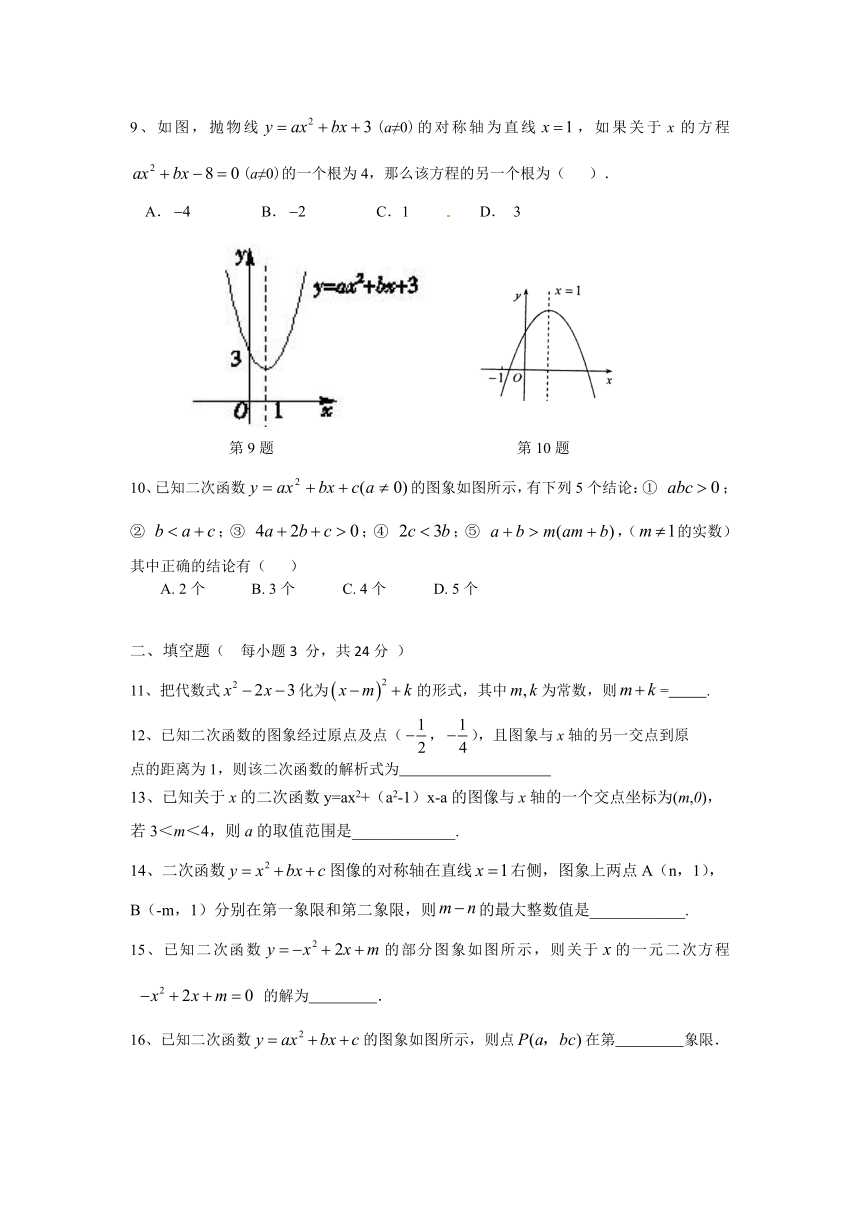
9、如图,抛物线(a≠0)的对称轴为直线,如果关于x的方程(a≠0)的一个根为4,那么该方程的另一个根为( ).
A. B. C.1 D. 3
第9题 第10题
10、已知二次函数的图象如图所示,有下列5个结论:① ;② ;③ ;④ ;⑤ ,(的实数)其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
填空题( 每小题3 分,共24分 )
11、把代数式化为的形式,其中为常数,则= .
12、已知二次函数的图象经过原点及点(,),且图象与x轴的另一交点到原
点的距离为1,则该二次函数的解析式为
13、已知关于x的二次函数y=ax2+(a2-1)x-a的图像与x轴的一个交点坐标为(m,0),若3<m<4,则a的取值范围是_____________.
14、二次函数图像的对称轴在直线右侧,图象上两点A(n,1),
B(-m,1)分别在第一象限和第二象限,则的最大整数值是____________.
15、已知二次函数的部分图象如图所示,则关于的一元二次方程 的解为 .
16、已知二次函数的图象如图所示,则点在第 象限.
(
(第
15
题)
) (
x
y
O
第
16
题
)
17、若函数的图象与x轴有且只有一个交点,则a的值为________.
18、如图,一段抛物线:,记为,它与x轴交于点O,;将绕点旋转180°得,交x轴于点;将绕点旋转180°得,交x轴于点;…如此进行下去,直至得,若P(28.5,m)在第15段抛物线上,则m的值为__________
三、解答题( 6+6+6+9+9+10+10+10=66分 )
19、已知二次函数
(1)若b=c,是否存在实数x,使得相应的的值为1?请说明理由;
(2)若b=c-2,在-2≤x≤2上的最小值是-3,求的值.
20、在平面直角坐标系xOy中,直线y=﹣x+n经过点A(﹣4,2),分别与x,y轴交于点B,C,抛物线y=x2﹣2mx+m2﹣n的顶点为D.
(1)求点B,C的坐标;
(2)①直接写出抛物线顶点D的坐标(用含m的式子表示);
②若抛物线y=x2﹣2mx+m2﹣n与线段BC有公共点,求m的取值范围.
21、如图,一张正三角形的纸片的边长为2cm,分别是边(含端点)上的点,设,的面积为。
(1)求关于的函数表达式和自变量的取值范围﹒
(2)求的面积的最大值和最小值﹒
22、在平面直角坐标系xOy中,抛物线y=mx2-2mx-3 (m≠0)与y轴交于点A,其对称轴与x轴交于点B顶点为C点.
(1)求点A和点B的坐标;
(2)若∠ACB=45°,求此抛物线的表达式;
(3)在(2)的条件下,垂直于轴的直线与抛物线交于点P(x1,y1)和Q(x2,y2),与直线AB交于点N(x3,y3),若x323、如图,在平面直角坐标系xOy中,二次函数y=﹣+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣+bx+c的图象分别交于B,C两点,点B在第一象限.
(1)求二次函数y=﹣+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
24、若抛物线L:y=ax2+bx+c(a,b,c是常数,且abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称此抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点在反比例函数y=(x<0)的图象上,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在 y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
25、新星电子科技公司积极应对新冠肺炎引起的经济滑坡,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?
26、根据学习函数的经验“先确定自变量取值范围,然后取值、描点,画出大致图像,再观察图像归纳性质”,对函数图象与性质进行了探究:
(1)写出自变量x的取值范围是 ;
(2)若下表是y与x的几组对应值(如下图所示),并在平面直角坐标系中,描出了表格对应值为坐标的点.
x … 2 1 0 1 2 3 4 …
y … 2 4 2 m …
①表中m的值为 ;
②根据描出的点,画出函数的大致图象;
(3)根据函数图象,
①请写出函数的两条性质;
②若此函数的图像与直线y=a的交点有2个,那么a的取值范围.
【知识梳理】
1. 二次函数的图像特征与a,b,c的关系
(1)a的符号与绝对值的大小<=>抛物线的开口方向与大小
(2)c的值就是图象与y轴交点的纵坐标
(3)对称轴与a,b的关系(简记口诀“左同右异”)
(4)的符号与抛物线与x轴交点的个数的关系
2. 图像的平移(简记为“上加下减、左加右减”)
3. 二次函数(a≠0)的性质
条件 图像 增减性 最值
a的符号 >0 =0 <0 对称轴为
a>0
a<0
4. 二次函数与一元二次方程的关系(判断依据:)
【基础巩固】
选择题( 每小题3 分,共30分 )
1、抛物线的顶点坐标是( )
(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
2、二次函数的最小值是( ).
2 B.1 C.-3 D.
3、在平面直角坐标系中,将二次函数的图象向上平移2个单位,所得图象的解析式为( )
A. B. C. D.
4、在同一坐标系中一次函数和二次函数的图象可能为( )
(
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
)
5、二次函数y=(x﹣a)(x﹣b)﹣2,(a<b)的图象与x轴交点的横坐标为m,n,且m<n,则a,b,m,n的大小关系是( )
A.m<a<b<n B.a<m<b<n C.a<m<n<b D.m<a<n<b
6、已知函数,且,若不论取何正数时,函数值都随自变量的增大而减小,则满足条件的的取值范围是( )
A. -4≤x≤-2 B.-2<x≤- C.1<x≤3 D.3≤x<5
7、已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:①二次函数y1有最大值;②二次函数y1的图象关于直线x=﹣1对称;
③当x=﹣2时,二次函数y1的值大于0;④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.其中正确的是( )
A.①③ B.①④ C.②③ D.②④
第7题 第8题
8、在同一坐标系下,抛物线y1=﹣x2+4x和直线y2=2x的图象如图所示,那么不等式﹣x2+4x>2x的解集是( )
A.x<0 B.0<x<2 C.x>2 D.x<0或 x>2
9、如图,抛物线(a≠0)的对称轴为直线,如果关于x的方程(a≠0)的一个根为4,那么该方程的另一个根为( ).
A. B. C.1 D. 3
第9题 第10题
10、已知二次函数的图象如图所示,有下列5个结论:① ;② ;③ ;④ ;⑤ ,(的实数)其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
填空题( 每小题3 分,共24分 )
11、把代数式化为的形式,其中为常数,则= .
12、已知二次函数的图象经过原点及点(,),且图象与x轴的另一交点到原
点的距离为1,则该二次函数的解析式为
13、已知关于x的二次函数y=ax2+(a2-1)x-a的图像与x轴的一个交点坐标为(m,0),若3<m<4,则a的取值范围是_____________.
14、二次函数图像的对称轴在直线右侧,图象上两点A(n,1),
B(-m,1)分别在第一象限和第二象限,则的最大整数值是____________.
15、已知二次函数的部分图象如图所示,则关于的一元二次方程 的解为 .
16、已知二次函数的图象如图所示,则点在第 象限.
(
(第
15
题)
) (
x
y
O
第
16
题
)
17、若函数的图象与x轴有且只有一个交点,则a的值为________.
18、如图,一段抛物线:,记为,它与x轴交于点O,;将绕点旋转180°得,交x轴于点;将绕点旋转180°得,交x轴于点;…如此进行下去,直至得,若P(28.5,m)在第15段抛物线上,则m的值为__________
三、解答题( 6+6+6+9+9+10+10+10=66分 )
19、已知二次函数
(1)若b=c,是否存在实数x,使得相应的的值为1?请说明理由;
(2)若b=c-2,在-2≤x≤2上的最小值是-3,求的值.
20、在平面直角坐标系xOy中,直线y=﹣x+n经过点A(﹣4,2),分别与x,y轴交于点B,C,抛物线y=x2﹣2mx+m2﹣n的顶点为D.
(1)求点B,C的坐标;
(2)①直接写出抛物线顶点D的坐标(用含m的式子表示);
②若抛物线y=x2﹣2mx+m2﹣n与线段BC有公共点,求m的取值范围.
21、如图,一张正三角形的纸片的边长为2cm,分别是边(含端点)上的点,设,的面积为。
(1)求关于的函数表达式和自变量的取值范围﹒
(2)求的面积的最大值和最小值﹒
22、在平面直角坐标系xOy中,抛物线y=mx2-2mx-3 (m≠0)与y轴交于点A,其对称轴与x轴交于点B顶点为C点.
(1)求点A和点B的坐标;
(2)若∠ACB=45°,求此抛物线的表达式;
(3)在(2)的条件下,垂直于轴的直线与抛物线交于点P(x1,y1)和Q(x2,y2),与直线AB交于点N(x3,y3),若x3
(1)求二次函数y=﹣+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
24、若抛物线L:y=ax2+bx+c(a,b,c是常数,且abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称此抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点在反比例函数y=(x<0)的图象上,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在 y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
25、新星电子科技公司积极应对新冠肺炎引起的经济滑坡,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?
26、根据学习函数的经验“先确定自变量取值范围,然后取值、描点,画出大致图像,再观察图像归纳性质”,对函数图象与性质进行了探究:
(1)写出自变量x的取值范围是 ;
(2)若下表是y与x的几组对应值(如下图所示),并在平面直角坐标系中,描出了表格对应值为坐标的点.
x … 2 1 0 1 2 3 4 …
y … 2 4 2 m …
①表中m的值为 ;
②根据描出的点,画出函数的大致图象;
(3)根据函数图象,
①请写出函数的两条性质;
②若此函数的图像与直线y=a的交点有2个,那么a的取值范围.
