湘教版数学八年级上第一次月考(含答案)
文档属性
| 名称 | 湘教版数学八年级上第一次月考(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 386.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 08:57:42 | ||
图片预览



文档简介
湘教版数学八年级上
第一次月考评价卷
一、选择题(每小题3分,共30分)
1.在,,,,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,直线EF经过AC的中点O,交AB于点E,交CD于点F,下列不能使△AOE≌△COF的条件为( )
A.∠A=∠C B.AB∥CD C.AE=CF D.OE=OF
3.下列计算结果正确的是( ).
A. B.
C. D.
4.如图,等腰△ABC底边BC的长为4cm,面积为12cm2,腰AB的垂直平分线EF交AC与点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为( )
A.4cm B.6cm C.8cm D.10cm
5.已知x2+mx+25是完全平方式,则m的值为( )
A. 10 B. ±10 C. 20 D. ±20
6. 已知 ,则 的值是( )
A. B. C. 2 D. -2
7.以下说法中,正确的是( )
①等腰三角形的一边长4cm,一边长9cm,则它的周长为17 cm或22cm;
②三角形的一个外角,等于两个内角的和;
③有两边和一角对应相等的两个三角形全等;
④三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.①②③ B.①③ C.②④ D.④
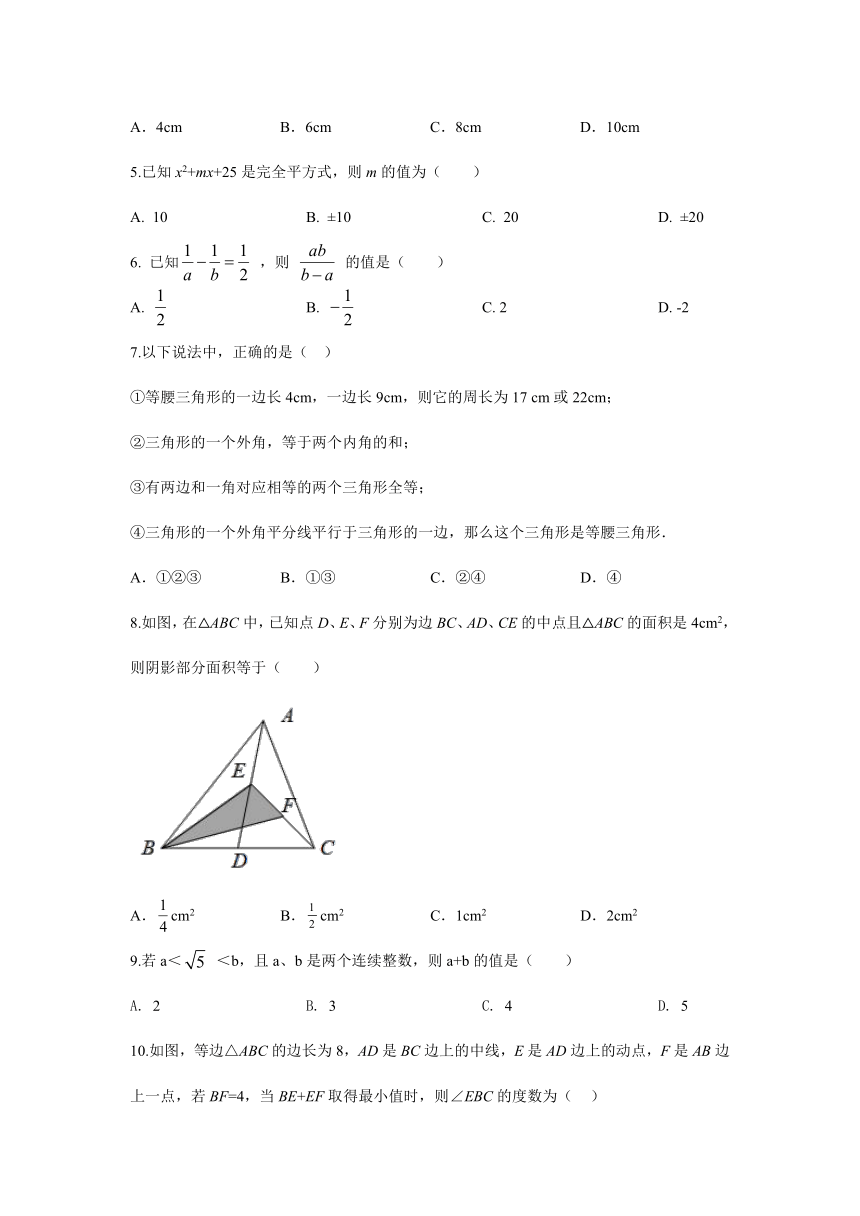
8.如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点且△ABC的面积是4cm2,则阴影部分面积等于( )
A.cm2 B.cm2 C.1cm2 D.2cm2
9.若a< <b,且a、b是两个连续整数,则a+b的值是( )
A. 2 B. 3 C. 4 D. 5
10.如图,等边△ABC的边长为8,AD是BC边上的中线,E是AD边上的动点,F是AB边上一点,若BF=4,当BE+EF取得最小值时,则∠EBC的度数为( )
A.15° B.25° C.30° D.45°
二.填空题(共8小题,满分24分,每小题3分)
11.化简的结果是__________.
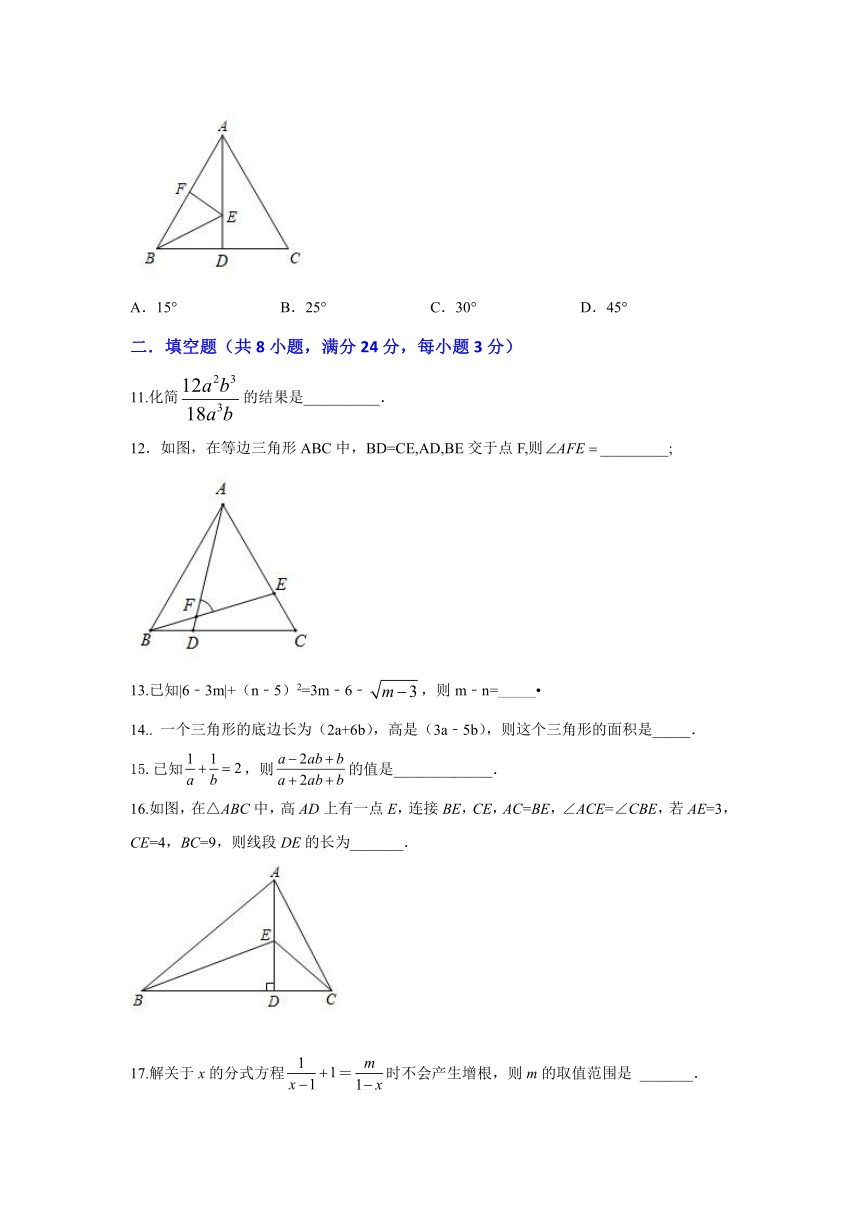
12.如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则_________;
13.已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n=_____
14.. 一个三角形的底边长为(2a+6b),高是(3a﹣5b),则这个三角形的面积是_____.
15.已知,则的值是_____________.
16.如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
17.解关于x的分式方程=时不会产生增根,则m的取值范围是 _______.
18.观察下列按顺序排列的等式:,试猜想第n个等式(n为正整数):an=_____.
三、解答题(共66分)
19.(本题6分)计算:
(1) ; (2) .
20.(本题6分)求代数式的值,其中x=1.
21.(本题8分)如图,已知:在中,,、是的角平分线,交于点O求证:.
22.(本题8分)有一道题:“先化简,再求值: 其中,”.小玲做题时把“”错抄成了“”,但她的计算结果也是正确的,请你解释这是怎么回事?
23.(本题8分)如图,在中,,分别为,边的垂直平分线,连接,.
(1)若,求的度数;
(2)判断与之间的数量关系,并说明理由.
24.(本题10分)某商家预测一种应季衬衫能畅销市场,就4000元购进一批这种衬衫,这种衬衫面市后果然供不应求,商家又8800元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元.
(1)该商家购进的两批衬衫数量分别是多少件?
(2)商家销售这种衬衫时每件定价都是60元,经过一段时间后,根据市场销售情况,商家决定对最后剩余的20件衬衫进行打折出售,要使这两批衬衫全部售出后的总利润不少于4960元,则最后剩余的20件衬衫出售至多可打几折?
25.(本题10分)有这样一段叙述:“要比较与的大小,可以先求出与的差,再看这个差是正数、负数还是0”.由此可见,要比较两个代数式的值的大小,只要考查它们的差即可.
问题:甲、乙两人两次同时去同一个商店购买水果(假设两次购水果的单价不同,分别为元,元,),甲每次购水果20千克,乙每次购水果用去20元.
(1)用含,的代数式表示:甲两次购水果共付 元;乙两次共购 千克水果;甲两次购水果的平均单价为 元/千克,乙两次购水果的平均单价为 元/千克;
(2)现规定:谁购水果的平均单价低,谁购水果的方式就合算,请你判断甲、乙两人的购水果方式哪一个更合算?并说明理由.
26.(本题10分)在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
参考答案
一、1.B 2.C 3.C 4.C 5.B 6.C 7.D 8.C 9.D 10.C
二、11. 12.60° 13.﹣2 14.3a2+4ab﹣15b2 15.0 16.
17.m≠﹣1 18.
三、19.(1)12;(2)
20.,0
21.证明:如图,在上取一点H,使,连接.
∵是的角平分线,
∴,
在和中,∴,
∴,
∵是的角平分线,
∴,
∵,
∴,
∵、是的角平分线,
∴,
∴,
在和中,
∴,
∴,
∵,
∴.
22.原式= (x+2)(x﹣2)
=x2+4,
若小玲做题时把“x=﹣3”错抄成了“x=3”,得到x2=9不变,故计算结果正确.
23.(1)解:连接并延长BD交AC于点G,
∵,分别为,边的垂直平分线
∴
∴
∵是△BDC的外角
∴
∵是△BDA的外角
∴
∴
(2)
,理由如下:
连接并延长BD交AC于点G,
∵,分别为,边的垂直平分线
∴
∴CD=AD
∴∠ACD=∠CAD
∴
∵是△BDC的外角
∴
∵是△BDA的外角
∴
∴
∴
.
24.(1)设该商家第一批购进这种衬衫x件,则第二批购进这种衬衫2x件,
依题意得:,
解得:x=100,
经检验,x=100是原方程的解,且符合题意,
∴2x=2×100=200.
答:该商家第一批购进这种衬衫100件,第二批购进这种衬衫200件.
(2)设最后剩余的20件衬衫打m折出售,
依题意得:60×(100+200 20)+60××20 4000 8800≥4960,
解得:m≥8.
答:最后剩余的20件衬衫出售至多可打八折.
25.(1)甲每次购买水果共需要付款(20x+20y)元;
乙两次共购买()千克的水果;
甲两次购水果的平均单价Q1=,乙两次购水果的平均单价Q2=40÷()=;
故答案为:(20x+20y);();;
(2)乙购买水果的方式更合算些,理由为:
Q1 Q2=-=,
∵x≠y,x>0,y>0,
∴(x y)2>0,2(x+y)>0,
∴>0,
∴Q1 Q2>0,即Q1>Q2,
∴乙购买水果的方式更合算些.
26.(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
∴∠ABC=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∵∠ACE+∠ACB=β,
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②如图1:当点D在射线BC上时,α+β=180°,
连接CE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,
即:∠BCE+∠BAC=180°,
∴α+β=180°,
如图2:当点D在射线BC的反向延长线上时,α=β.
连接BE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠ABD=∠ACE=∠ACB+∠BCE,
∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,
∵∠BAC=180° ∠ABC ∠ACB,
∴∠BAC=∠BCE.
∴α=β;
综上所述:点D在直线BC上移动,α+β=180°或α=β.
第一次月考评价卷
一、选择题(每小题3分,共30分)
1.在,,,,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.如图,直线EF经过AC的中点O,交AB于点E,交CD于点F,下列不能使△AOE≌△COF的条件为( )
A.∠A=∠C B.AB∥CD C.AE=CF D.OE=OF
3.下列计算结果正确的是( ).
A. B.
C. D.
4.如图,等腰△ABC底边BC的长为4cm,面积为12cm2,腰AB的垂直平分线EF交AC与点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为( )
A.4cm B.6cm C.8cm D.10cm
5.已知x2+mx+25是完全平方式,则m的值为( )
A. 10 B. ±10 C. 20 D. ±20
6. 已知 ,则 的值是( )
A. B. C. 2 D. -2
7.以下说法中,正确的是( )
①等腰三角形的一边长4cm,一边长9cm,则它的周长为17 cm或22cm;
②三角形的一个外角,等于两个内角的和;
③有两边和一角对应相等的两个三角形全等;
④三角形的一个外角平分线平行于三角形的一边,那么这个三角形是等腰三角形.
A.①②③ B.①③ C.②④ D.④
8.如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点且△ABC的面积是4cm2,则阴影部分面积等于( )
A.cm2 B.cm2 C.1cm2 D.2cm2
9.若a< <b,且a、b是两个连续整数,则a+b的值是( )
A. 2 B. 3 C. 4 D. 5
10.如图,等边△ABC的边长为8,AD是BC边上的中线,E是AD边上的动点,F是AB边上一点,若BF=4,当BE+EF取得最小值时,则∠EBC的度数为( )
A.15° B.25° C.30° D.45°
二.填空题(共8小题,满分24分,每小题3分)
11.化简的结果是__________.
12.如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则_________;
13.已知|6﹣3m|+(n﹣5)2=3m﹣6﹣,则m﹣n=_____
14.. 一个三角形的底边长为(2a+6b),高是(3a﹣5b),则这个三角形的面积是_____.
15.已知,则的值是_____________.
16.如图,在△ABC中,高AD上有一点E,连接BE,CE,AC=BE,∠ACE=∠CBE,若AE=3,CE=4,BC=9,则线段DE的长为_______.
17.解关于x的分式方程=时不会产生增根,则m的取值范围是 _______.
18.观察下列按顺序排列的等式:,试猜想第n个等式(n为正整数):an=_____.
三、解答题(共66分)
19.(本题6分)计算:
(1) ; (2) .
20.(本题6分)求代数式的值,其中x=1.
21.(本题8分)如图,已知:在中,,、是的角平分线,交于点O求证:.
22.(本题8分)有一道题:“先化简,再求值: 其中,”.小玲做题时把“”错抄成了“”,但她的计算结果也是正确的,请你解释这是怎么回事?
23.(本题8分)如图,在中,,分别为,边的垂直平分线,连接,.
(1)若,求的度数;
(2)判断与之间的数量关系,并说明理由.
24.(本题10分)某商家预测一种应季衬衫能畅销市场,就4000元购进一批这种衬衫,这种衬衫面市后果然供不应求,商家又8800元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了4元.
(1)该商家购进的两批衬衫数量分别是多少件?
(2)商家销售这种衬衫时每件定价都是60元,经过一段时间后,根据市场销售情况,商家决定对最后剩余的20件衬衫进行打折出售,要使这两批衬衫全部售出后的总利润不少于4960元,则最后剩余的20件衬衫出售至多可打几折?
25.(本题10分)有这样一段叙述:“要比较与的大小,可以先求出与的差,再看这个差是正数、负数还是0”.由此可见,要比较两个代数式的值的大小,只要考查它们的差即可.
问题:甲、乙两人两次同时去同一个商店购买水果(假设两次购水果的单价不同,分别为元,元,),甲每次购水果20千克,乙每次购水果用去20元.
(1)用含,的代数式表示:甲两次购水果共付 元;乙两次共购 千克水果;甲两次购水果的平均单价为 元/千克,乙两次购水果的平均单价为 元/千克;
(2)现规定:谁购水果的平均单价低,谁购水果的方式就合算,请你判断甲、乙两人的购水果方式哪一个更合算?并说明理由.
26.(本题10分)在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
参考答案
一、1.B 2.C 3.C 4.C 5.B 6.C 7.D 8.C 9.D 10.C
二、11. 12.60° 13.﹣2 14.3a2+4ab﹣15b2 15.0 16.
17.m≠﹣1 18.
三、19.(1)12;(2)
20.,0
21.证明:如图,在上取一点H,使,连接.
∵是的角平分线,
∴,
在和中,∴,
∴,
∵是的角平分线,
∴,
∵,
∴,
∵、是的角平分线,
∴,
∴,
在和中,
∴,
∴,
∵,
∴.
22.原式= (x+2)(x﹣2)
=x2+4,
若小玲做题时把“x=﹣3”错抄成了“x=3”,得到x2=9不变,故计算结果正确.
23.(1)解:连接并延长BD交AC于点G,
∵,分别为,边的垂直平分线
∴
∴
∵是△BDC的外角
∴
∵是△BDA的外角
∴
∴
(2)
,理由如下:
连接并延长BD交AC于点G,
∵,分别为,边的垂直平分线
∴
∴CD=AD
∴∠ACD=∠CAD
∴
∵是△BDC的外角
∴
∵是△BDA的外角
∴
∴
∴
.
24.(1)设该商家第一批购进这种衬衫x件,则第二批购进这种衬衫2x件,
依题意得:,
解得:x=100,
经检验,x=100是原方程的解,且符合题意,
∴2x=2×100=200.
答:该商家第一批购进这种衬衫100件,第二批购进这种衬衫200件.
(2)设最后剩余的20件衬衫打m折出售,
依题意得:60×(100+200 20)+60××20 4000 8800≥4960,
解得:m≥8.
答:最后剩余的20件衬衫出售至多可打八折.
25.(1)甲每次购买水果共需要付款(20x+20y)元;
乙两次共购买()千克的水果;
甲两次购水果的平均单价Q1=,乙两次购水果的平均单价Q2=40÷()=;
故答案为:(20x+20y);();;
(2)乙购买水果的方式更合算些,理由为:
Q1 Q2=-=,
∵x≠y,x>0,y>0,
∴(x y)2>0,2(x+y)>0,
∴>0,
∴Q1 Q2>0,即Q1>Q2,
∴乙购买水果的方式更合算些.
26.(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
∴∠ABC=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=90°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,
∴∠BAC ∠DAC=∠DAE ∠DAC.
即∠BAD=∠CAE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∵∠ACE+∠ACB=β,
∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,
∴α+β=180°;
②如图1:当点D在射线BC上时,α+β=180°,
连接CE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,
即:∠BCE+∠BAC=180°,
∴α+β=180°,
如图2:当点D在射线BC的反向延长线上时,α=β.
连接BE,
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∴∠ABD=∠ACE=∠ACB+∠BCE,
∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,
∵∠BAC=180° ∠ABC ∠ACB,
∴∠BAC=∠BCE.
∴α=β;
综上所述:点D在直线BC上移动,α+β=180°或α=β.
同课章节目录
