福建省漳浦县2022-2023学年高中学业水平合格性考试数学模拟试卷(一)(含答案)
文档属性
| 名称 | 福建省漳浦县2022-2023学年高中学业水平合格性考试数学模拟试卷(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 651.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 00:00:00 | ||
图片预览




文档简介
漳浦县2022-2023学年高中学业水平合格性考试数学模拟试卷(一)
(考试时间:90分钟 满分:100分)
第I卷(选择题 45分)
一、单项选择题(本大题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1.已知集合,,则 ( )
A. B. C. D.
2.已知命题和命题,则p是q的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知复数z满足,则|z|= ( )
A.1 B. C.2 D.2
4.已知向量,,且,则 ( )
A. B. C. D.
5.已知在上是偶函数,且满足,当时,,则
( )
A. B. C. D.
6.化简的结果为 ( )
A. B. C. D.
7.设,则,, ,,的大小关系是 ( )
A. B. C. D.
8.在矩形ABCD中,,点E为CD的中点(如图1),沿AE将折起到处,使得平面平面ABCE(如图2),则直线PC与平面ABCE所成角的正切值为 ( )
A. B.
C. D. 1
9.下图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,则由直方图得到的25%分位数为 ( )
A.66.5 B.67
C.67.5 D.68
10.将函数图象上所有点的横坐标缩短到原来的倍纵坐标不变,再向左平移个单位长度,得到函数的图象,若在上单调递减,则实数的取值范围为 ( )
A. B. C. D.
二、多项选择题(本大题有5小题,每小题3分,共15分.在每小题给出的选项中,有多项符合题目要求.全部选对的得3分,部分选对的得2分,有选错的得0分)
11.已知集合,.若,则实数m的值可取 ( )
A.0 B.1 C.2 D.3
12.若,且,则 ( )
A. B. C. D.
13.在△ABC中,根据下列条件解三角形,其中恰有一解的是 ( )
A. B.
C. D.
14.已知事件A,B,且,则下列判断正确的是 ( )
A.如果,那么
B.如果A与B互斥,那么
C.如果A与B相互独立,那么
D.如果A与B相互独立,那么
15.已知定义在上的函数的图象是连续不断的,且满足以下条件:
①,;②,,当时,;
③.则下列选项成立的是 ( )
A. B.若,则
C.若,则 D.,,使得
第II卷(非选择题 55分)
三、填空题(本大题有5小题,每小题3分,共15分)
16.已知复数为纯虚数,则实数a =______.
17.函数的定义域是________.
18.已知扇形OAB的圆心角为4,其周长是6cm,则该扇形的面积是________.
19.已知定义在上的奇函数,当时,,
当时,________.
20.如图,已知球C与圆锥VO的侧面和底面均相切,且球心C在线段VO上,圆锥VO的底面半径为1,母线长为2,则球C的表面积为___ __.
四、解答题(本大题有5小题,共40分.解答应写出文字说明、证明过程或演算步骤)
21.(本小题满分6分)已知函数.
(1)求函数的单调减区间;
(2)当时,求函数的值域.
22.(本小题满分8分)如图,已知平面,,,点和分别为和的中点.
(1)求证: 平面;
(2)判断是否与平面平行,并说明理由.
23.(本小题满分8分)已知函数.
(1)判断在区间上的单调性,并用定义法证明;
(2)已知不等式恒成立,求正数的取值范围.
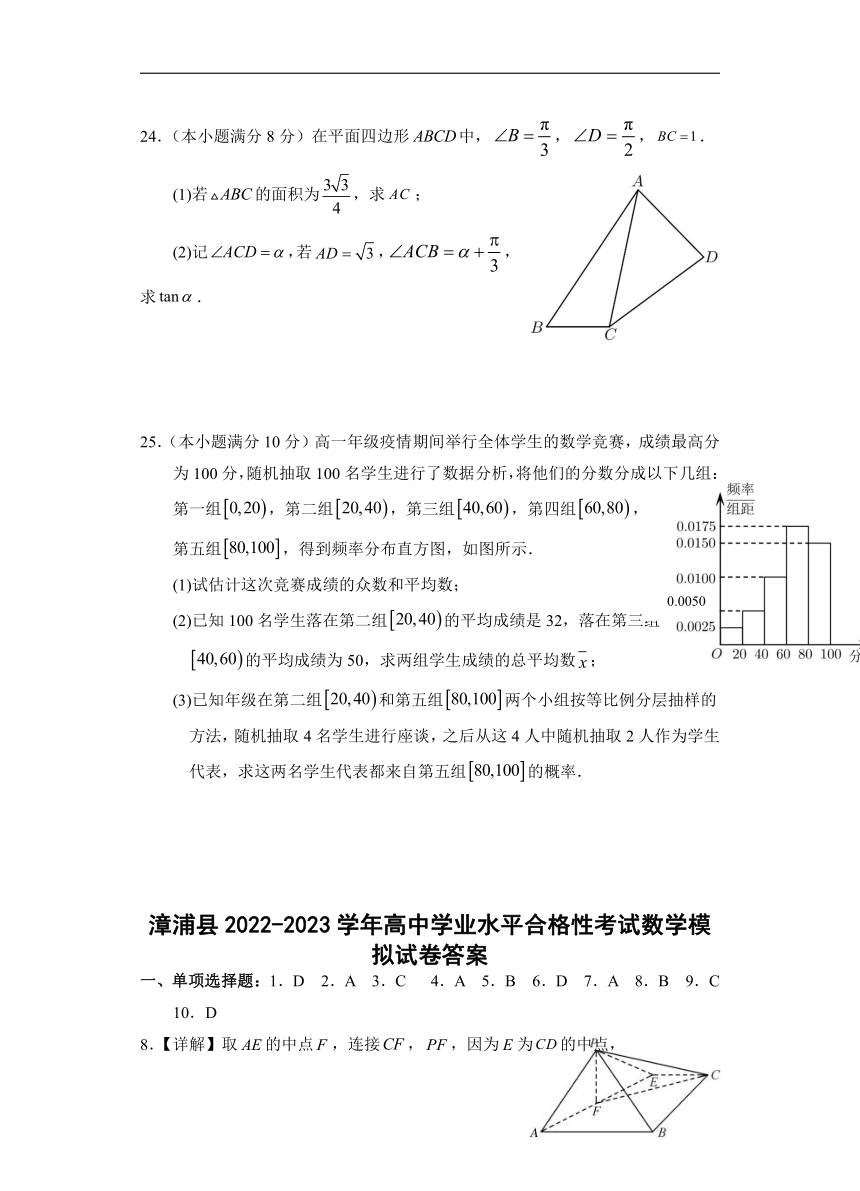
24.(本小题满分8分)在平面四边形中,,,.
(1)若的面积为,求;
(2)记,若,,求.
25.(本小题满分10分)高一年级疫情期间举行全体学生的数学竞赛,成绩最高分为100分,随机抽取100名学生进行了数据分析,将他们的分数分成以下几组:
第一组,第二组,第三组,第四组,
第五组,得到频率分布直方图,如图所示.
(1)试估计这次竞赛成绩的众数和平均数;
(2)已知100名学生落在第二组的平均成绩是32,落在第三组
的平均成绩为50,求两组学生成绩的总平均数;
(3)已知年级在第二组和第五组两个小组按等比例分层抽样的方法,随机抽取4名学生进行座谈,之后从这4人中随机抽取2人作为学生代表,求这两名学生代表都来自第五组的概率.
漳浦县2022-2023学年高中学业水平合格性考试数学模拟试卷答案
一、单项选择题:1.D 2.A 3.C 4.A 5.B 6.D 7.A 8.B 9.C 10.D
8.【详解】取的中点,连接,,因为为的中点,
所以,即,所以,
又平面平面,平面平面,平面,
所以平面,所以为所求线面角,,
在中,由余弦定理得,
,,所以.故选:B.
9.【详解】第一组的频率为,前两组的频率之和为,
知25%分位数在第二组内,故25%分位数为.故选:C.
10.【详解】将函数图象上所有点的横坐标缩短到原来的倍纵坐标不变,得到,再向左平移个单位长度,得到函数的图象,
即,若在上单调递减,
则的周期,即,得,
由,,得,,
即,即的单调递减区间为,,
若在上单调递减,则,,
即,,当时,,即的取值范围是.故选:D.
二、多项选择题:11.AD 12.AC 13.BC 14.ABD 15.CD
12.【详解】对于A,,且,,解得,故A正确;
对于B,不妨取,则不满足,故B错误;
对于C,,且,,当且仅当时,等号成立,,故C正确;对于D,,且,,
当且仅当,即时等号成立,∵-3=,
∴,故D错误.故选:AC
15.【详解】根据题中条件知,函数为R上的偶函数;根据题中条件知,函数在上单调递增.根据函数的单调性得,,选项A错误;
是R上的偶函数,且在上单调递增
时, ,解得,选项B错误;
或
解得或,即 时,,选项C正确;
根据偶函数的单调性可得,函数在上单调递减
在R上有最小值,故选项D正确.故选:CD.
三、填空题:16. 17. 18. 19. 20.
四、解答题
21.解:(1),
令,,解得,,
所以函数的单调减区间是,;
(2)由,得,
所以,所以,所以函数的值域为.
22.解:(1) ,为中点,,
平面,,平面,
,又,平面,
平面,
(2) 平面,理由如下:连接,在中,
和分别是和的中点,,
又平面,平面,平面.
23.解:(1) ,,且,则
,
由,,得,又由,得,
于是,即,所以在区间上单调递增.
(2)因为恒成立,且,,
由(1)得在区间上单调递增,故恒成立.
等价于在上恒成立,令,所以,
则有在恒成立,令,,则 ,所以,所以正数的取值范围为.
24.解:(1),解得,
由余弦定理得,因此,.
(2)在中,,在中,,
由正弦定理得,即,
所以,,
即,故.
25.解:(1)由图可得,众数为,第一组,第二组,第三组,第四组,第五组所占的频率分别为,,,,,
故平均数为
(2)由图可得,第二组的人数为人,第三组的人数为,
故.
(3)由题,第二组和第五组的人数比为,故在第二组和第五组分别抽1人和3人.记第二组中的1人为,第五组中的3人分别为,则这4人中随机抽取2人作为学生代表,所有可能的情况有,,,,,共6种情况,其中这两名学生代表都来自第五组的有,,3种情况.设“从这4人中随机抽取2人作为学生代表,这两名学生代表都来自第五组”的事件为,则.
试卷第1页,共3页
(考试时间:90分钟 满分:100分)
第I卷(选择题 45分)
一、单项选择题(本大题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1.已知集合,,则 ( )
A. B. C. D.
2.已知命题和命题,则p是q的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.已知复数z满足,则|z|= ( )
A.1 B. C.2 D.2
4.已知向量,,且,则 ( )
A. B. C. D.
5.已知在上是偶函数,且满足,当时,,则
( )
A. B. C. D.
6.化简的结果为 ( )
A. B. C. D.
7.设,则,, ,,的大小关系是 ( )
A. B. C. D.
8.在矩形ABCD中,,点E为CD的中点(如图1),沿AE将折起到处,使得平面平面ABCE(如图2),则直线PC与平面ABCE所成角的正切值为 ( )
A. B.
C. D. 1
9.下图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图,则由直方图得到的25%分位数为 ( )
A.66.5 B.67
C.67.5 D.68
10.将函数图象上所有点的横坐标缩短到原来的倍纵坐标不变,再向左平移个单位长度,得到函数的图象,若在上单调递减,则实数的取值范围为 ( )
A. B. C. D.
二、多项选择题(本大题有5小题,每小题3分,共15分.在每小题给出的选项中,有多项符合题目要求.全部选对的得3分,部分选对的得2分,有选错的得0分)
11.已知集合,.若,则实数m的值可取 ( )
A.0 B.1 C.2 D.3
12.若,且,则 ( )
A. B. C. D.
13.在△ABC中,根据下列条件解三角形,其中恰有一解的是 ( )
A. B.
C. D.
14.已知事件A,B,且,则下列判断正确的是 ( )
A.如果,那么
B.如果A与B互斥,那么
C.如果A与B相互独立,那么
D.如果A与B相互独立,那么
15.已知定义在上的函数的图象是连续不断的,且满足以下条件:
①,;②,,当时,;
③.则下列选项成立的是 ( )
A. B.若,则
C.若,则 D.,,使得
第II卷(非选择题 55分)
三、填空题(本大题有5小题,每小题3分,共15分)
16.已知复数为纯虚数,则实数a =______.
17.函数的定义域是________.
18.已知扇形OAB的圆心角为4,其周长是6cm,则该扇形的面积是________.
19.已知定义在上的奇函数,当时,,
当时,________.
20.如图,已知球C与圆锥VO的侧面和底面均相切,且球心C在线段VO上,圆锥VO的底面半径为1,母线长为2,则球C的表面积为___ __.
四、解答题(本大题有5小题,共40分.解答应写出文字说明、证明过程或演算步骤)
21.(本小题满分6分)已知函数.
(1)求函数的单调减区间;
(2)当时,求函数的值域.
22.(本小题满分8分)如图,已知平面,,,点和分别为和的中点.
(1)求证: 平面;
(2)判断是否与平面平行,并说明理由.
23.(本小题满分8分)已知函数.
(1)判断在区间上的单调性,并用定义法证明;
(2)已知不等式恒成立,求正数的取值范围.
24.(本小题满分8分)在平面四边形中,,,.
(1)若的面积为,求;
(2)记,若,,求.
25.(本小题满分10分)高一年级疫情期间举行全体学生的数学竞赛,成绩最高分为100分,随机抽取100名学生进行了数据分析,将他们的分数分成以下几组:
第一组,第二组,第三组,第四组,
第五组,得到频率分布直方图,如图所示.
(1)试估计这次竞赛成绩的众数和平均数;
(2)已知100名学生落在第二组的平均成绩是32,落在第三组
的平均成绩为50,求两组学生成绩的总平均数;
(3)已知年级在第二组和第五组两个小组按等比例分层抽样的方法,随机抽取4名学生进行座谈,之后从这4人中随机抽取2人作为学生代表,求这两名学生代表都来自第五组的概率.
漳浦县2022-2023学年高中学业水平合格性考试数学模拟试卷答案
一、单项选择题:1.D 2.A 3.C 4.A 5.B 6.D 7.A 8.B 9.C 10.D
8.【详解】取的中点,连接,,因为为的中点,
所以,即,所以,
又平面平面,平面平面,平面,
所以平面,所以为所求线面角,,
在中,由余弦定理得,
,,所以.故选:B.
9.【详解】第一组的频率为,前两组的频率之和为,
知25%分位数在第二组内,故25%分位数为.故选:C.
10.【详解】将函数图象上所有点的横坐标缩短到原来的倍纵坐标不变,得到,再向左平移个单位长度,得到函数的图象,
即,若在上单调递减,
则的周期,即,得,
由,,得,,
即,即的单调递减区间为,,
若在上单调递减,则,,
即,,当时,,即的取值范围是.故选:D.
二、多项选择题:11.AD 12.AC 13.BC 14.ABD 15.CD
12.【详解】对于A,,且,,解得,故A正确;
对于B,不妨取,则不满足,故B错误;
对于C,,且,,当且仅当时,等号成立,,故C正确;对于D,,且,,
当且仅当,即时等号成立,∵-3=,
∴,故D错误.故选:AC
15.【详解】根据题中条件知,函数为R上的偶函数;根据题中条件知,函数在上单调递增.根据函数的单调性得,,选项A错误;
是R上的偶函数,且在上单调递增
时, ,解得,选项B错误;
或
解得或,即 时,,选项C正确;
根据偶函数的单调性可得,函数在上单调递减
在R上有最小值,故选项D正确.故选:CD.
三、填空题:16. 17. 18. 19. 20.
四、解答题
21.解:(1),
令,,解得,,
所以函数的单调减区间是,;
(2)由,得,
所以,所以,所以函数的值域为.
22.解:(1) ,为中点,,
平面,,平面,
,又,平面,
平面,
(2) 平面,理由如下:连接,在中,
和分别是和的中点,,
又平面,平面,平面.
23.解:(1) ,,且,则
,
由,,得,又由,得,
于是,即,所以在区间上单调递增.
(2)因为恒成立,且,,
由(1)得在区间上单调递增,故恒成立.
等价于在上恒成立,令,所以,
则有在恒成立,令,,则 ,所以,所以正数的取值范围为.
24.解:(1),解得,
由余弦定理得,因此,.
(2)在中,,在中,,
由正弦定理得,即,
所以,,
即,故.
25.解:(1)由图可得,众数为,第一组,第二组,第三组,第四组,第五组所占的频率分别为,,,,,
故平均数为
(2)由图可得,第二组的人数为人,第三组的人数为,
故.
(3)由题,第二组和第五组的人数比为,故在第二组和第五组分别抽1人和3人.记第二组中的1人为,第五组中的3人分别为,则这4人中随机抽取2人作为学生代表,所有可能的情况有,,,,,共6种情况,其中这两名学生代表都来自第五组的有,,3种情况.设“从这4人中随机抽取2人作为学生代表,这两名学生代表都来自第五组”的事件为,则.
试卷第1页,共3页
同课章节目录
