相交线、垂线期末复习[下学期]
文档属性
| 名称 | 相交线、垂线期末复习[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 744.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-15 00:00:00 | ||
图片预览

文档简介
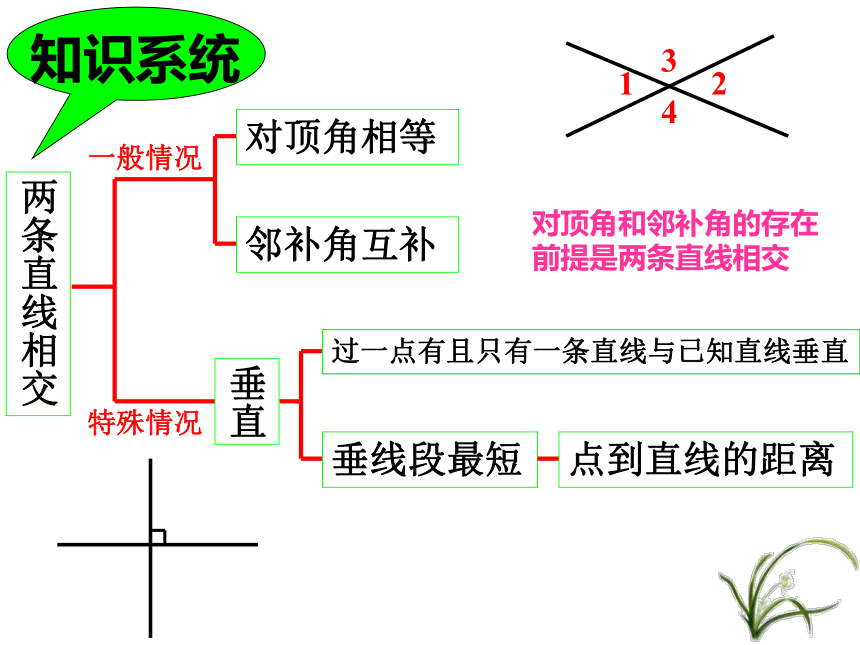
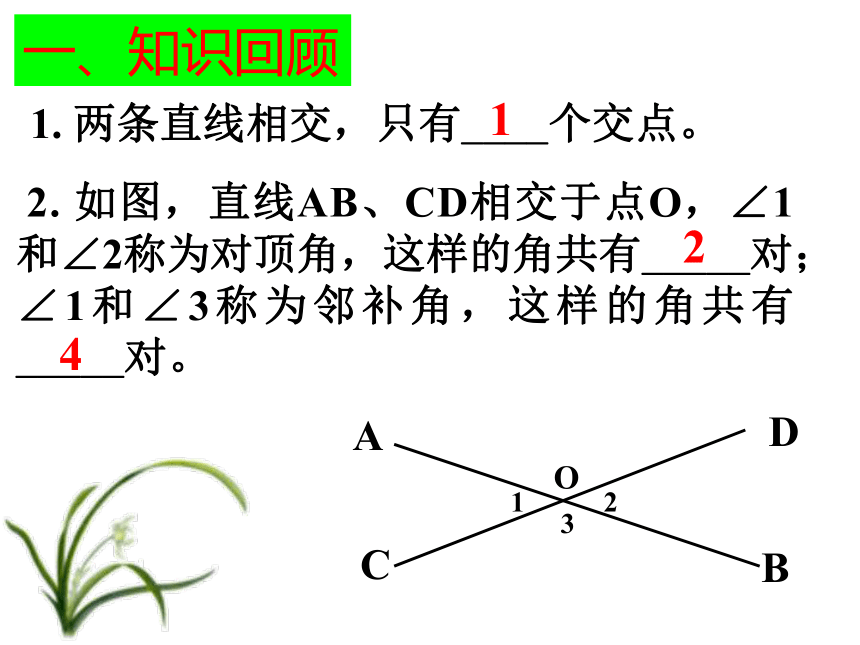
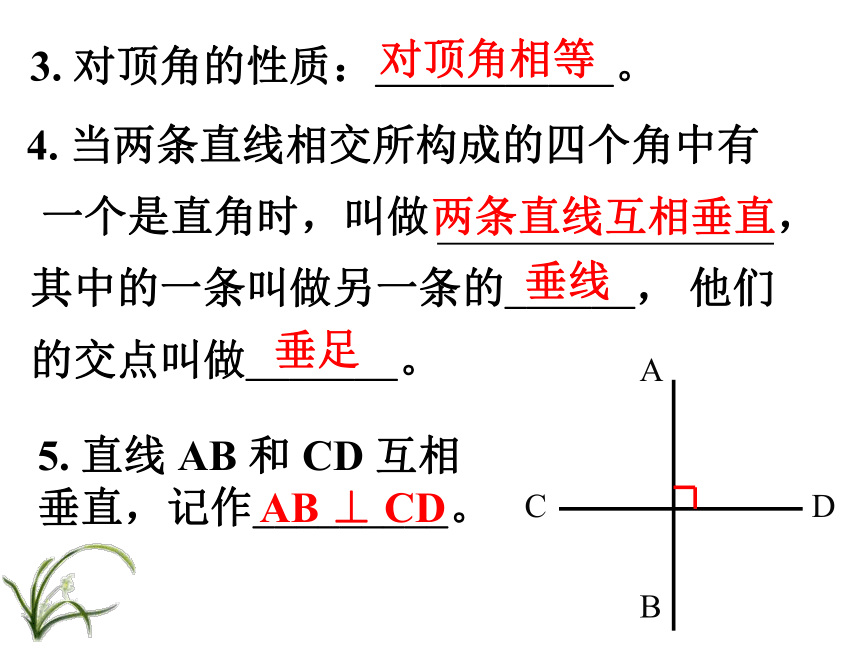
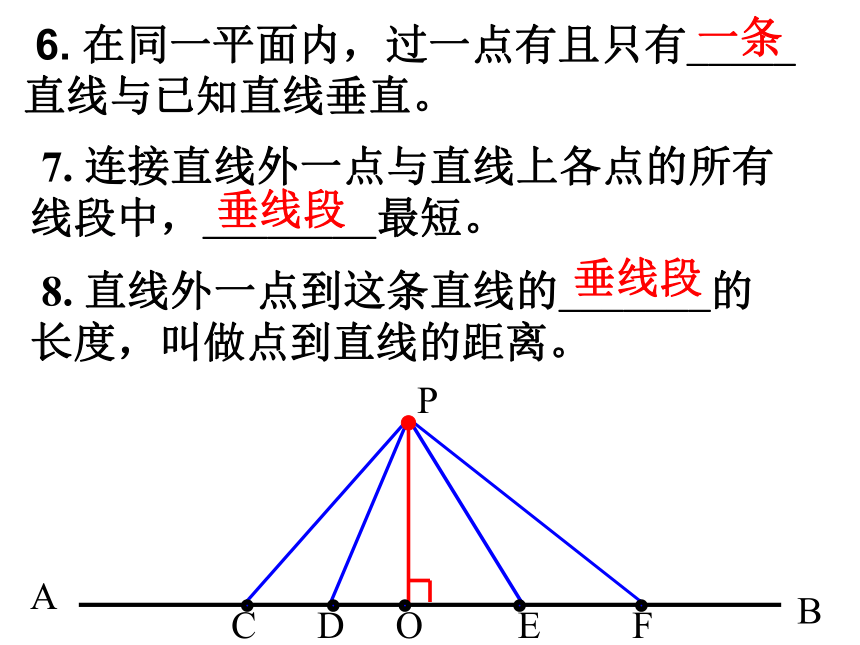
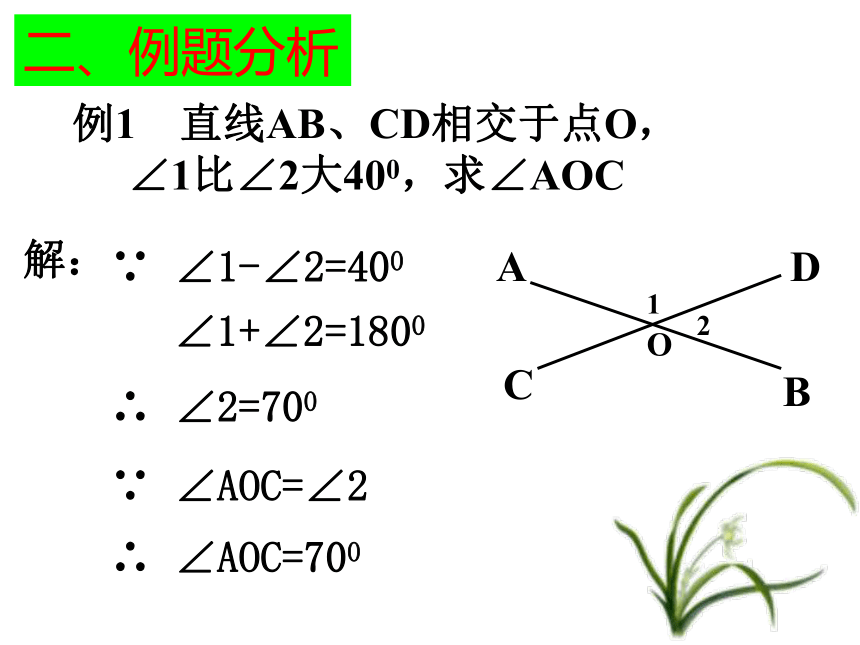
课件22张PPT。第一课 相交线、垂线复习第一课 相交线、垂线复习泽国第三中学两条直线相交一般情况特殊情况对顶角相等邻补角互补垂直垂线段最短点到直线的距离过一点有且只有一条直线与已知直线垂直知识系统对顶角和邻补角的存在前提是两条直线相交一、知识回顾 1. 两条直线相交,只有____个交点。 1 2. 如图,直线AB、CD相交于点O,∠1和∠2称为对顶角,这样的角共有_____对;∠1和∠3称为邻补角,这样的角共有_____对。 243. 对顶角的性质:___________。 对顶角相等两条直线互相垂直垂足垂线5. 直线 AB 和 CD 互相垂直,记作_________。 AB ⊥ CD 6. 在同一平面内,过一点有且只有_____直线与已知直线垂直。 一条 7. 连接直线外一点与直线上各点的所有线段中,________最短。 垂线段 8. 直线外一点到这条直线的_______的长度,叫做点到直线的距离。 垂线段PBA二、例题分析 例1??? 直线AB、CD相交于点O,
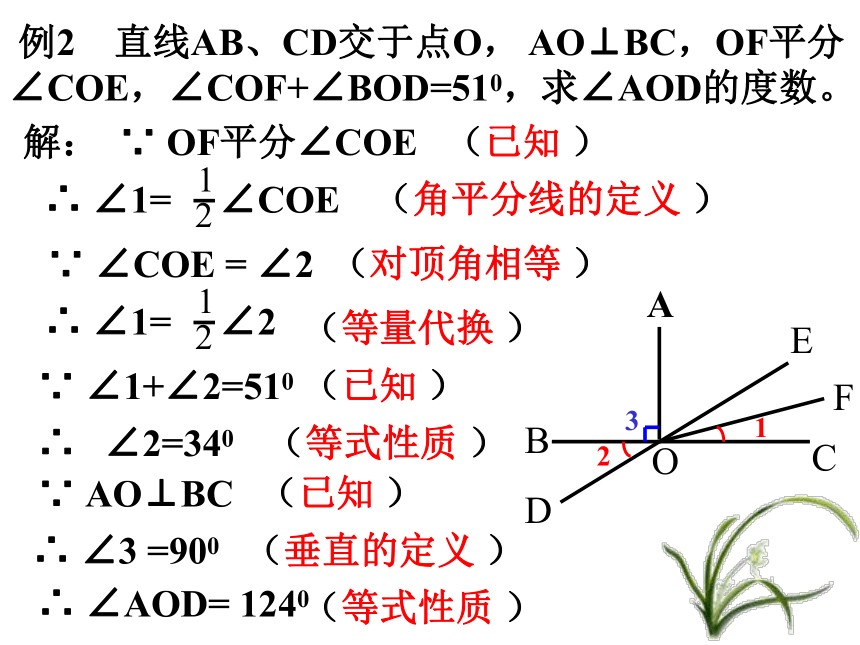
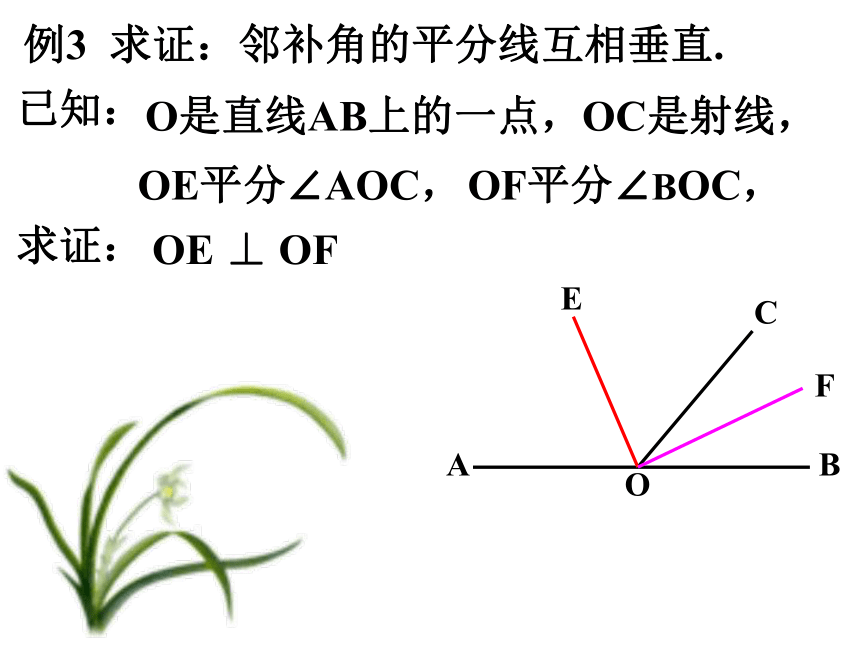
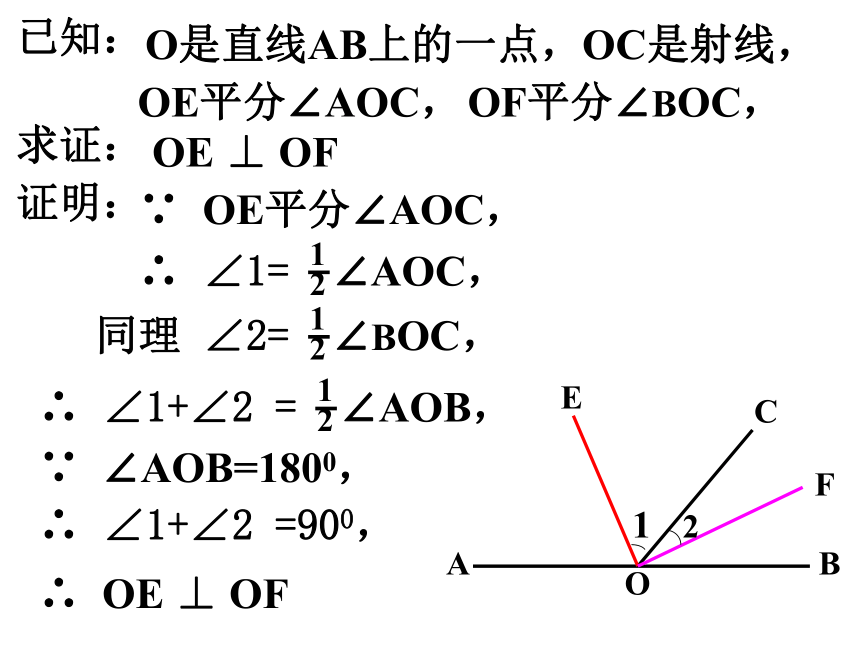
∠1比∠2大400,求∠AOC 解:∵ ∠1-∠2=400∠1+∠2=1800∴ ∠2=700∵ ∠AOC=∠2∴ ∠AOC=700 例2 直线AB、CD交于点O, AO⊥BC,OF平分∠COE,∠COF+∠BOD=510,求∠AOD的度数。∵ AO⊥BC解: ∵ OF平分∠COE12 ∵ ∠COE = ∠2 ∵ ∠1+∠2=510 ∴ ∠2=340 ∴ ∠AOD= 1240 ∴ ∠3 =9003(已知 )(角平分线的定义 )(对顶角相等 )(等量代换 )(已知 )(等式性质 )(已知 )(垂直的定义 )(等式性质 )例3 求证:邻补角的平分线互相垂直. OCEF已知:O是直线AB上的一点,OC是射线,OE平分∠AOC,OF平分∠BOC,求证:OE ⊥ OF证明:∵ OE平分∠AOC,∵ ∠AOB=1800,∴ ∠1+∠2 =900, ∴ OE ⊥ OF三、课内练习 16°对顶角相等35014501450 3. 如图所示,AB与CD相交所成的四
个角中,∠1的邻补角是___________,
∠1的对顶角_______. ∠2和∠4∠34. 如图,三条直线AB,CD,EF相交于一点O,且∠1=500,∠2=600,则∠3等于( )
A. 50° B. 60° C. 70° D. 80° 4C 5. ∵ ∠1= 90° (已知)
∴ AB ____ CD ( ) ⊥垂直的定义42 6. 点C到直线AB的距离是_______cm;
点B到直线CD的距离是________cm;
点_____到直线_______的距离是4 cm. ABC 7. 在灌溉时,要把河AB中的水引到农田P处,如何挖渠能使渠道最短? M解:作PM ⊥ AB,垂足为M.沿垂线段PM挖渠,能使渠道最短。8. 直线AB、CD相交于点O,OE平分∠BOD,
∠AOE=1500,求 ∠AOC. 解:∵ ∠AOE +∠1 =1800,∠AOE =1500,∴ ∠1=300 ∵ OE平分∠BOD∴ ∠BOD=2∠1 ∵ ∠AOC= ∠BOD∴ ∠AOC=2∠1 =600四、课外作业 1. 下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A. 1个 B. 2个 C. 3个 D. 4个 2. 如图OA⊥OC,OB⊥OD,且∠BOC=α,则∠AOD=________ B1800-α?3. 如图,OE⊥CD,OF平分∠BOC,∠AOC=30 0,则∠BOE= 0,∠COF= 0,∠EOF= 0,∠AOE= 0。 756015120?4.????? 已知: 直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD的度数。 5.??已知:直线AB、CD相交于点O,OE⊥CD于点O,∠AOE = 55 0,求:∠BOD的度数. 6.如图,OE平分∠BOC,∠BOE=65 0,求∠AOD和∠AOC。 ?7. 如图,∠AOC=500, ∠BOE :∠EOD=2 :3,
求∠EOD ?
8. 求证:对顶角的平分线互为反向延长线 9. 若4条不同的直线相交于一点,则图中共有几对对顶角?若n条不同的直线相交于一点呢? 10. 在平面内,4条不同的直线最多有几个交点?n条不同的直线最多有几个交点? 再 见祝大家学习愉快再见!
∠1比∠2大400,求∠AOC 解:∵ ∠1-∠2=400∠1+∠2=1800∴ ∠2=700∵ ∠AOC=∠2∴ ∠AOC=700 例2 直线AB、CD交于点O, AO⊥BC,OF平分∠COE,∠COF+∠BOD=510,求∠AOD的度数。∵ AO⊥BC解: ∵ OF平分∠COE12 ∵ ∠COE = ∠2 ∵ ∠1+∠2=510 ∴ ∠2=340 ∴ ∠AOD= 1240 ∴ ∠3 =9003(已知 )(角平分线的定义 )(对顶角相等 )(等量代换 )(已知 )(等式性质 )(已知 )(垂直的定义 )(等式性质 )例3 求证:邻补角的平分线互相垂直. OCEF已知:O是直线AB上的一点,OC是射线,OE平分∠AOC,OF平分∠BOC,求证:OE ⊥ OF证明:∵ OE平分∠AOC,∵ ∠AOB=1800,∴ ∠1+∠2 =900, ∴ OE ⊥ OF三、课内练习 16°对顶角相等35014501450 3. 如图所示,AB与CD相交所成的四
个角中,∠1的邻补角是___________,
∠1的对顶角_______. ∠2和∠4∠34. 如图,三条直线AB,CD,EF相交于一点O,且∠1=500,∠2=600,则∠3等于( )
A. 50° B. 60° C. 70° D. 80° 4C 5. ∵ ∠1= 90° (已知)
∴ AB ____ CD ( ) ⊥垂直的定义42 6. 点C到直线AB的距离是_______cm;
点B到直线CD的距离是________cm;
点_____到直线_______的距离是4 cm. ABC 7. 在灌溉时,要把河AB中的水引到农田P处,如何挖渠能使渠道最短? M解:作PM ⊥ AB,垂足为M.沿垂线段PM挖渠,能使渠道最短。8. 直线AB、CD相交于点O,OE平分∠BOD,
∠AOE=1500,求 ∠AOC. 解:∵ ∠AOE +∠1 =1800,∠AOE =1500,∴ ∠1=300 ∵ OE平分∠BOD∴ ∠BOD=2∠1 ∵ ∠AOC= ∠BOD∴ ∠AOC=2∠1 =600四、课外作业 1. 下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A. 1个 B. 2个 C. 3个 D. 4个 2. 如图OA⊥OC,OB⊥OD,且∠BOC=α,则∠AOD=________ B1800-α?3. 如图,OE⊥CD,OF平分∠BOC,∠AOC=30 0,则∠BOE= 0,∠COF= 0,∠EOF= 0,∠AOE= 0。 756015120?4.????? 已知: 直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD的度数。 5.??已知:直线AB、CD相交于点O,OE⊥CD于点O,∠AOE = 55 0,求:∠BOD的度数. 6.如图,OE平分∠BOC,∠BOE=65 0,求∠AOD和∠AOC。 ?7. 如图,∠AOC=500, ∠BOE :∠EOD=2 :3,
求∠EOD ?
8. 求证:对顶角的平分线互为反向延长线 9. 若4条不同的直线相交于一点,则图中共有几对对顶角?若n条不同的直线相交于一点呢? 10. 在平面内,4条不同的直线最多有几个交点?n条不同的直线最多有几个交点? 再 见祝大家学习愉快再见!
