2022-2023学年冀教版数学八年级上册 期中测试(含答案)
文档属性
| 名称 | 2022-2023学年冀教版数学八年级上册 期中测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 14:21:07 | ||
图片预览

文档简介
期中试卷
一、选择题(每小题3分,共36分)
1. 下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B. C. D.
3. 下列说法中不能判定是平行四边形的是( )
A. 一组对角相等且一组对边平行的四边形 B. 一组对边相等且另一组对边平行的四边形
C. 两组对角分别相等的四边形 D. 四条边相等的四边形
4. 化简结果是( )
A. B. C. D.
5. 下列每一组数据中的三个数值分别为三角形的三边长,则不能构成直角三角形的是( )
A. ,2, B. 6,8,10 C. 3,4,5 D. 5,12,13
6. 如图,是一高为2m,宽为1.5m的门框,李师傅有3块薄木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长2.8m,宽2.8m;③号木板长4m,宽2.4m.可以从这扇门通过的木板是()
A. ①号 B. ②号 C. ③号 D. 均不能通过
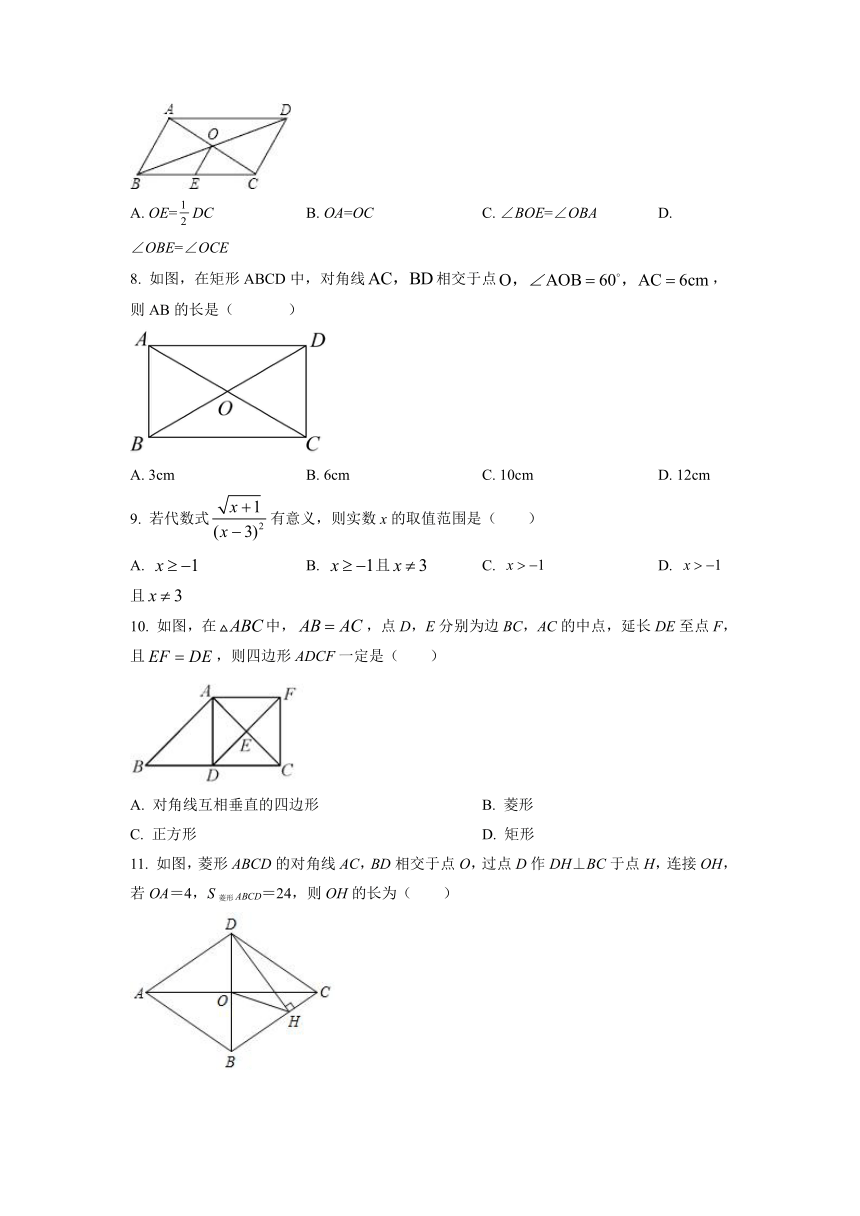
7. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A. OE=DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
8. 如图,在矩形ABCD中,对角线相交于点,则AB的长是( )
A. 3cm B. 6cm C. 10cm D. 12cm
9. 若代数式有意义,则实数x的取值范围是( )
A. B. 且 C. D. 且
10. 如图,在中,,点D,E分别为边BC,AC的中点,延长DE至点F,且,则四边形ADCF一定是( )
A. 对角线互相垂直的四边形 B. 菱形
C. 正方形 D. 矩形
11. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A B. 3 C. D.
12. 如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=BE,正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(每小题3分,共36分)
13. 把化为最简二次根式,结果是_________.
14. 直角三角形斜边长是6,直角边的长是5,则此直角三角形的另一直角边长为___.
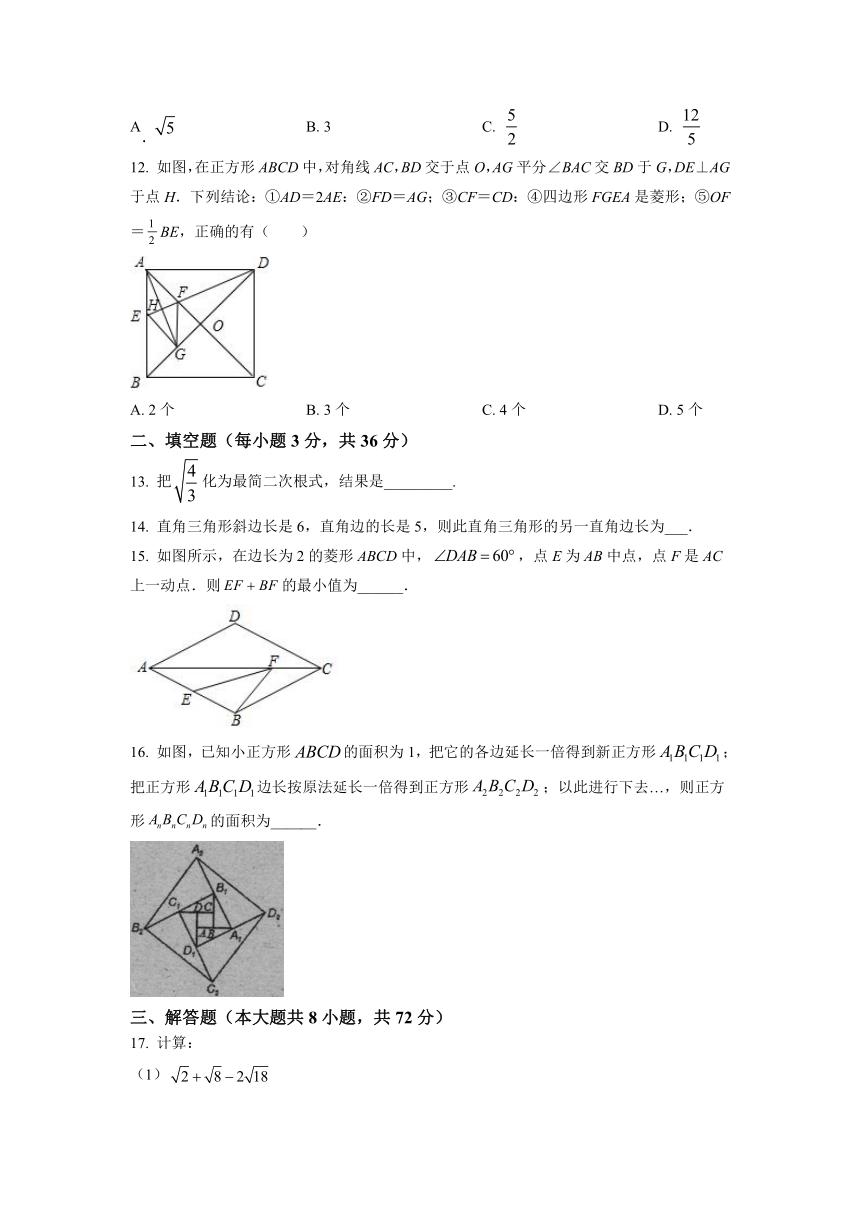
15. 如图所示,在边长为2的菱形ABCD中,,点E为AB中点,点F是AC上一动点.则的最小值为______.
16. 如图,已知小正方形的面积为1,把它的各边延长一倍得到新正方形;把正方形边长按原法延长一倍得到正方形;以此进行下去…,则正方形的面积为______.
三、解答题(本大题共8小题,共72分)
17. 计算:
(1)
(2)
18. 先化简,再求值:,其中.
19. 如图,网格中的,若小方格边长为,请你根据所学的知识,
(1)判断什么形状?并说明理由;
(2)求的面积.
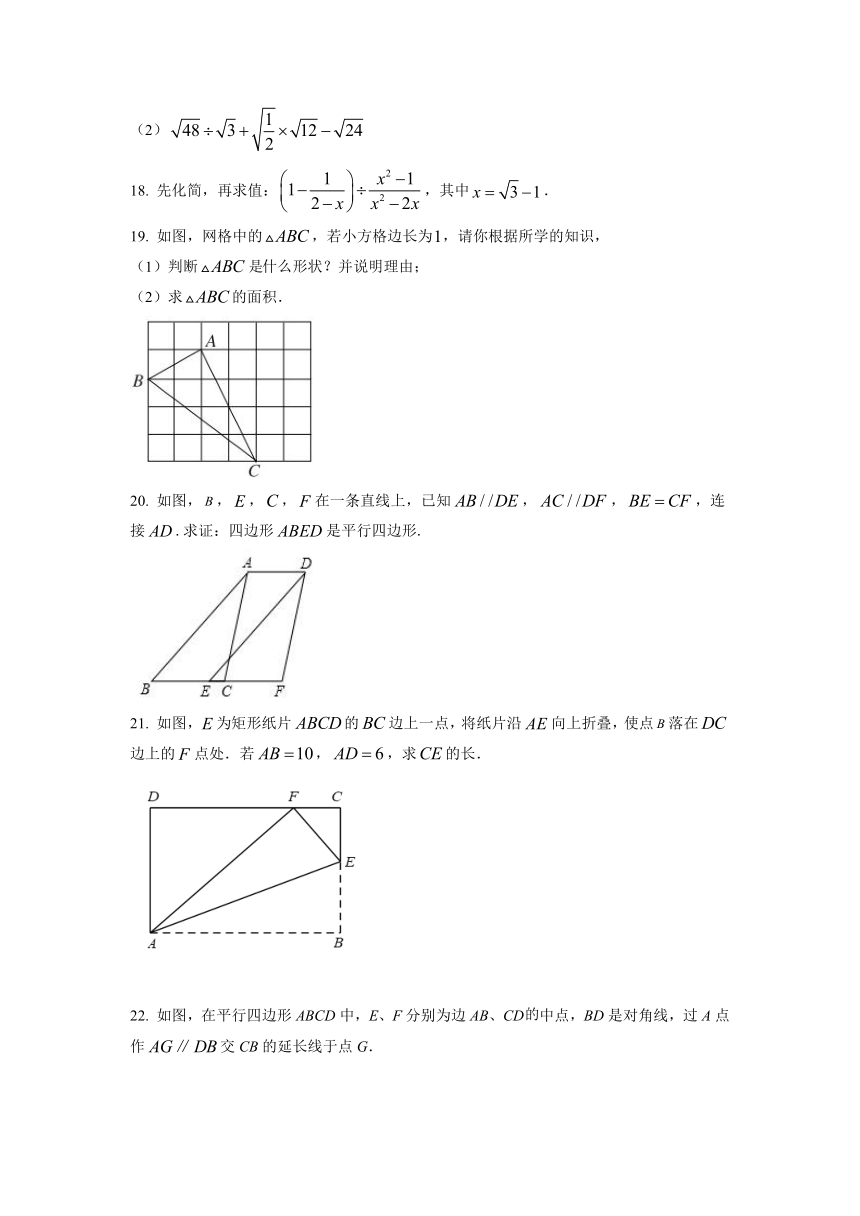
20. 如图,,,,在一条直线上,已知,,,连接.求证:四边形是平行四边形.
21. 如图,为矩形纸片的边上一点,将纸片沿向上折叠,使点落在边上的点处.若,,求的长.
22. 如图,在平行四边形ABCD中,E、F分别为边AB、CD中点,BD是对角线,过A点作交CB的延长线于点G.
(1)求证:.
(2)若,求证:四边形DEBF是菱形.
23. 如图,正方形ABCD中,,点E在CD上,且,将沿AE对折至,延长EF交BC于点G,连接AG、CF.
求证:≌;
求BG的长;
求的面积.
24. 如图①,在平面直角坐标系中,矩形边,.若不改变矩形的形状和大小,当矩形顶点在轴的正半轴上左右移动时,矩形的另一个顶点始终在轴的正半轴上随之上下移动.
(1)当时,求点的坐标;
(2)若点是的中点,连接,.当点在移动的过程中,等于多少度时,点,,,能组成平行四边形,并说明理由;求出此时点的坐标;
(3)连接,当点在移动的过程中,的长度是否存在最大值.如果存在,请直接写出结果;如果不存在,请简单说明理由.
2022年春来凤县实验中学八年级(下)数学期中试卷
一、选择题(每小题3分,共36分)
【1题答案】
【答案】D
【2题答案】
【答案】B
【3题答案】
【答案】B
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】D
【11题答案】
【答案】B
【12题答案】
【答案】C
二、填空题(每小题3分,共36分)
【13题答案】
【答案】
【14题答案】
【答案】
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题(本大题共8小题,共72分)
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】;
【19题答案】
【答案】(1)直角三角形,理由见解析;(2)5
【20题答案】
【答案】证明见解析.
【21题答案】
【答案】
【22题答案】
【答案】(1)见解析 (2)见解析
【23题答案】
【答案】(1)详见解析;(2)3;(3).
【24题答案】
【答案】(1)
(2),此时
(3)存在,
一、选择题(每小题3分,共36分)
1. 下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. B. C. D.
3. 下列说法中不能判定是平行四边形的是( )
A. 一组对角相等且一组对边平行的四边形 B. 一组对边相等且另一组对边平行的四边形
C. 两组对角分别相等的四边形 D. 四条边相等的四边形
4. 化简结果是( )
A. B. C. D.
5. 下列每一组数据中的三个数值分别为三角形的三边长,则不能构成直角三角形的是( )
A. ,2, B. 6,8,10 C. 3,4,5 D. 5,12,13
6. 如图,是一高为2m,宽为1.5m的门框,李师傅有3块薄木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长2.8m,宽2.8m;③号木板长4m,宽2.4m.可以从这扇门通过的木板是()
A. ①号 B. ②号 C. ③号 D. 均不能通过
7. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A. OE=DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
8. 如图,在矩形ABCD中,对角线相交于点,则AB的长是( )
A. 3cm B. 6cm C. 10cm D. 12cm
9. 若代数式有意义,则实数x的取值范围是( )
A. B. 且 C. D. 且
10. 如图,在中,,点D,E分别为边BC,AC的中点,延长DE至点F,且,则四边形ADCF一定是( )
A. 对角线互相垂直的四边形 B. 菱形
C. 正方形 D. 矩形
11. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4,S菱形ABCD=24,则OH的长为( )
A B. 3 C. D.
12. 如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=BE,正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(每小题3分,共36分)
13. 把化为最简二次根式,结果是_________.
14. 直角三角形斜边长是6,直角边的长是5,则此直角三角形的另一直角边长为___.
15. 如图所示,在边长为2的菱形ABCD中,,点E为AB中点,点F是AC上一动点.则的最小值为______.
16. 如图,已知小正方形的面积为1,把它的各边延长一倍得到新正方形;把正方形边长按原法延长一倍得到正方形;以此进行下去…,则正方形的面积为______.
三、解答题(本大题共8小题,共72分)
17. 计算:
(1)
(2)
18. 先化简,再求值:,其中.
19. 如图,网格中的,若小方格边长为,请你根据所学的知识,
(1)判断什么形状?并说明理由;
(2)求的面积.
20. 如图,,,,在一条直线上,已知,,,连接.求证:四边形是平行四边形.
21. 如图,为矩形纸片的边上一点,将纸片沿向上折叠,使点落在边上的点处.若,,求的长.
22. 如图,在平行四边形ABCD中,E、F分别为边AB、CD中点,BD是对角线,过A点作交CB的延长线于点G.
(1)求证:.
(2)若,求证:四边形DEBF是菱形.
23. 如图,正方形ABCD中,,点E在CD上,且,将沿AE对折至,延长EF交BC于点G,连接AG、CF.
求证:≌;
求BG的长;
求的面积.
24. 如图①,在平面直角坐标系中,矩形边,.若不改变矩形的形状和大小,当矩形顶点在轴的正半轴上左右移动时,矩形的另一个顶点始终在轴的正半轴上随之上下移动.
(1)当时,求点的坐标;
(2)若点是的中点,连接,.当点在移动的过程中,等于多少度时,点,,,能组成平行四边形,并说明理由;求出此时点的坐标;
(3)连接,当点在移动的过程中,的长度是否存在最大值.如果存在,请直接写出结果;如果不存在,请简单说明理由.
2022年春来凤县实验中学八年级(下)数学期中试卷
一、选择题(每小题3分,共36分)
【1题答案】
【答案】D
【2题答案】
【答案】B
【3题答案】
【答案】B
【4题答案】
【答案】B
【5题答案】
【答案】A
【6题答案】
【答案】C
【7题答案】
【答案】D
【8题答案】
【答案】A
【9题答案】
【答案】B
【10题答案】
【答案】D
【11题答案】
【答案】B
【12题答案】
【答案】C
二、填空题(每小题3分,共36分)
【13题答案】
【答案】
【14题答案】
【答案】
【15题答案】
【答案】
【16题答案】
【答案】
三、解答题(本大题共8小题,共72分)
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】;
【19题答案】
【答案】(1)直角三角形,理由见解析;(2)5
【20题答案】
【答案】证明见解析.
【21题答案】
【答案】
【22题答案】
【答案】(1)见解析 (2)见解析
【23题答案】
【答案】(1)详见解析;(2)3;(3).
【24题答案】
【答案】(1)
(2),此时
(3)存在,
同课章节目录
