22.2相似三角形的判定(1) 课件(共28张PPT)
文档属性
| 名称 | 22.2相似三角形的判定(1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 957.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 17:20:42 | ||
图片预览



文档简介
(共28张PPT)
沪科版 九年级上册
22.2相似三角形的判定(1)
用平行法判定三角形相似
教学目标
1.了解相似多边形的概念,掌握相似三角形及其相似比的概念;能用符号正确表示两个三角形相似;
2.会运用平行线法证明三角形相似.
教学重点:
用平行线法证明三角形相似.
教学难点:
用平行线法证明三角形相似.
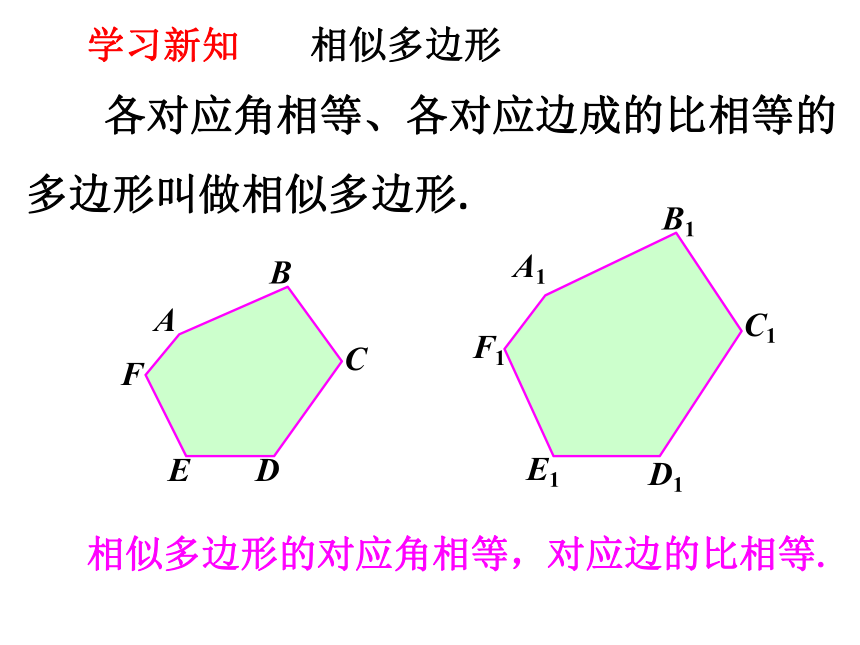
相似多边形
各对应角相等、各对应边成的比相等的
多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形的对应角相等,对应边的比相等.
学习新知
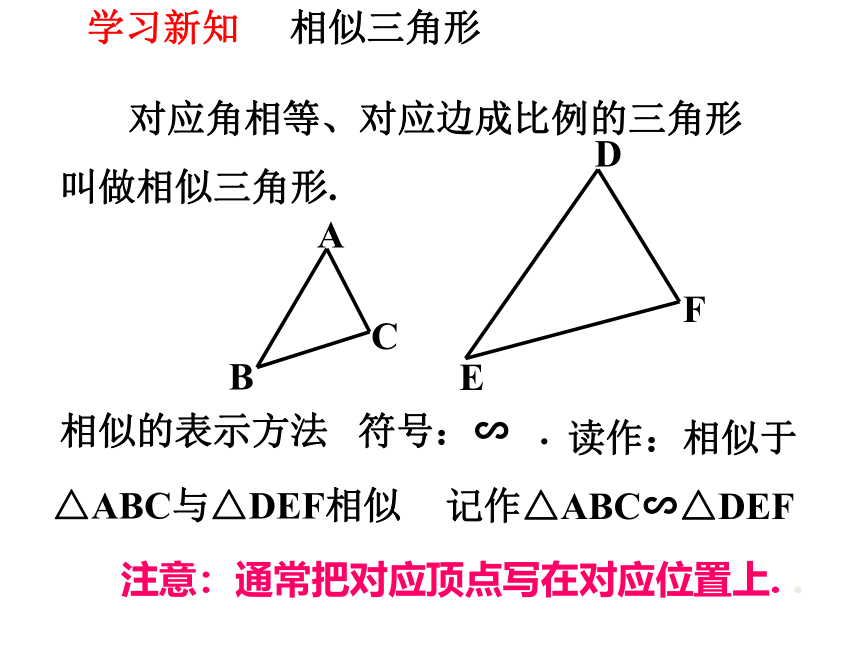
相似三角形
对应角相等、对应边成比例的三角形叫做相似三角形.
A
B
C
E
D
F
相似的表示方法
符号:∽ .
△ABC与△DEF相似
记作△ABC∽△DEF
注意:通常把对应顶点写在对应位置上. .
读作:相似于
学习新知
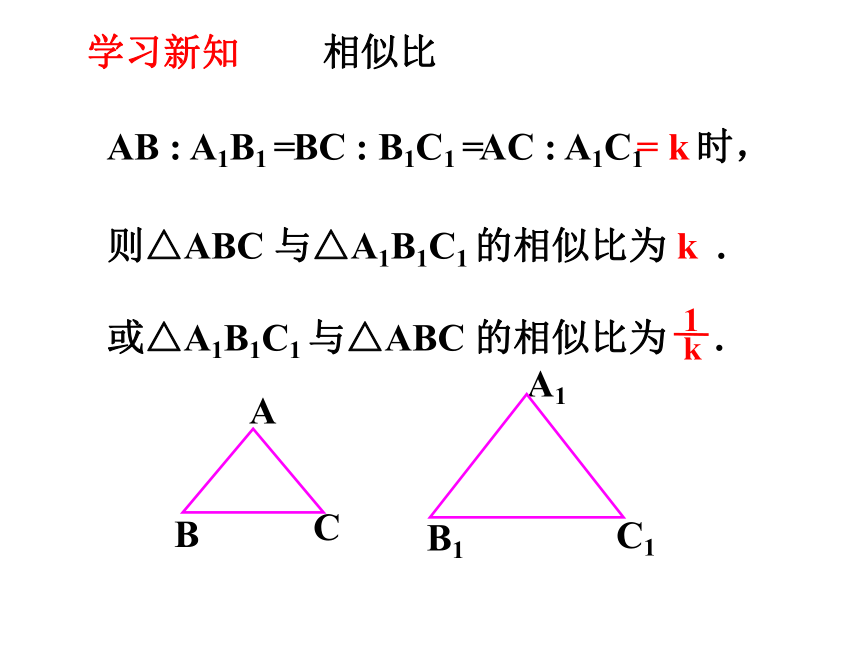
相似比
AB : A1B1 =
BC : B1C1 =
AC : A1C1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
1
k
学习新知
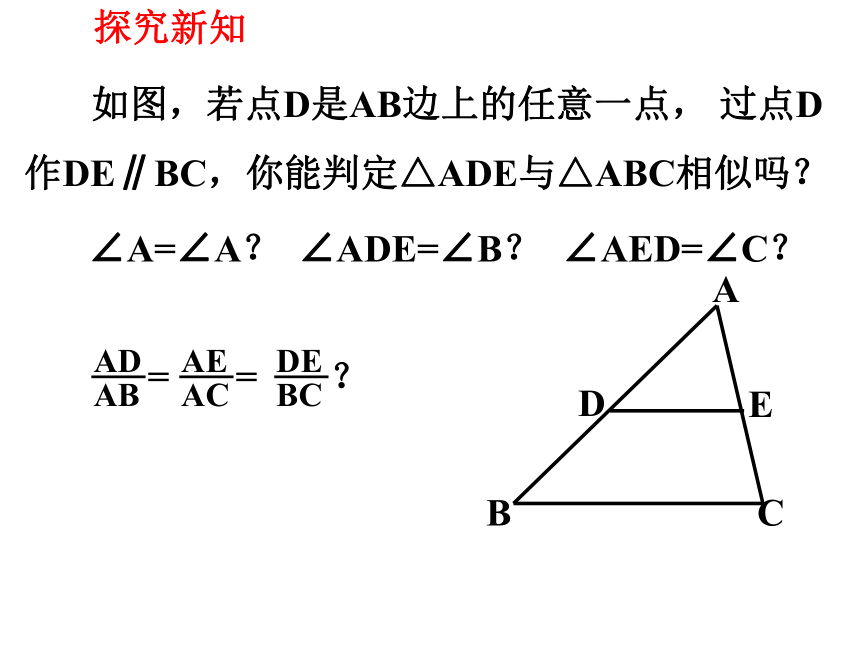
如图,若点D是AB边上的任意一点, 过点D作DE∥BC,你能判定△ADE与△ABC相似吗?
A
B
C
D
E
∠A=∠A?
∠ADE=∠B?
∠AED=∠C?
AD
AB
=
AE
AC
=
DE
BC
?
探究新知
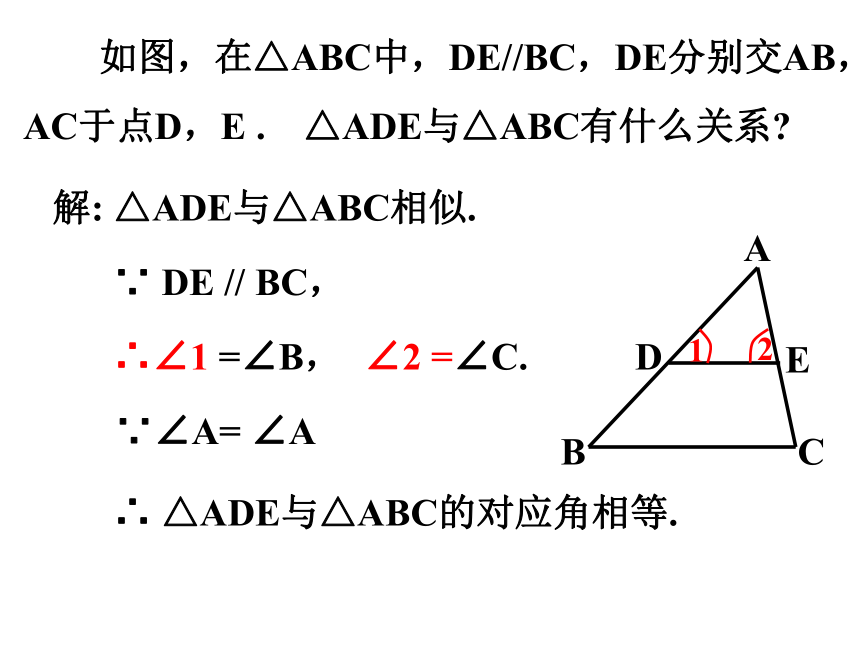
如图,在△ABC中,DE//BC,DE分别交AB,AC于点D,E . △ADE与△ABC有什么关系
A
B
C
D
E
解:
∵∠A= ∠A
∵ DE // BC,
∴∠1 =∠B,
∴ △ADE与△ABC的对应角相等.
△ADE与△ABC相似.
1
2
∠2 =∠C.
A
B
C
D
E
∵ DE // BC,
1
2
∴ 四边形DBFE是平行四边形.
∴ DE=BF .
∴ △ADE ∽ △ABC
过E作EF//AB交BC于F,
∴ △ADE与△ABC的对应边成比例.
∴ △ADE∽△ABC.
F
∵ DE // BC,
EF //AB,
AD
AB
∴
=
AE
AC
AE
AC
,
=
BF
BC
BF
BC
=
DE
BC
;
AD
AB
∴
=
AE
AC
=
DE
BC
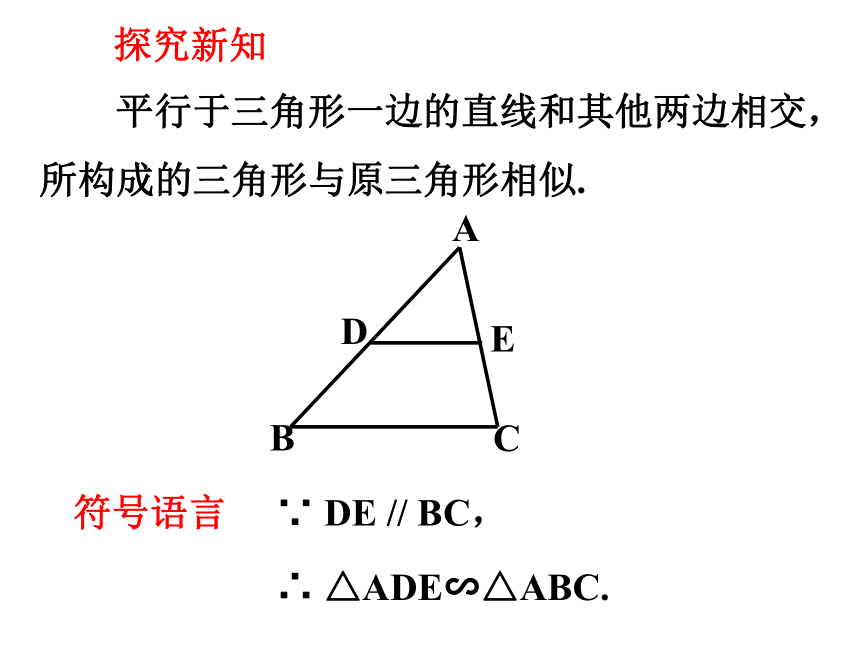
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
A
B
C
D
E
∵ DE // BC,
∴ △ADE∽△ABC.
符号语言
探究新知
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
定理可以适用以下三种情形:
∵DE∥BC
∴△ADE∽△ ABC
D
E
A
B
C
A
B
C
D
E
A
D
E
B
C
“8”字型
“A”字型
符号语言表示为:
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
N
M
如果再作 MN∥DE ,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形.
例1 如图, 已知DE∥BC,DF∥AC,请尽可能多地找出图中的相似三角形,并说明理由.
A
B
C
D
F
E
∵ DE∥BC
∵ DF∥AC
∴ ΔADE∽ΔDBF
∴ ΔDBF∽ΔABC
∴ ΔADE∽ΔABC
ΔADE∽ΔABC
∽ΔDBF
解:
例题解析
1.如图,在△ABC中,DE//BC,且AD=3,DB=2. 写出图中的相似三角形,并指出其相似比.
A
B
C
D
E
解:
∵ AD=3,
∴AB=AD+DB=3+2=5 ,
∴ △ADE与△ABC相似比为
△ADE与△ABC相似.
DB=2.
AD
AB
=
3
5
练习巩固
图中共有____对相似三角形.
2. 已知:如图,AB∥EF ∥CD,
3
△EOF∽△COD
AB∥EF
△AOB∽△FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____.
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
∵ DG//BC,
∴DG:BC=AD:AB.
AB=AD+DB=1+3=4
∴ ΔADG∽ΔABC,
例2 如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.
A
B
C
D
E
[解析] 要求线段DE的长
要求AC的长
DE∥BC
要求EC的长
AE:EC=AD:DB.
例2 如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.
A
B
C
D
E
∵ DE//BC,
∴AE:EC=AD:DB.
∵AD=EC,
∴AE:EC=EC:DB.
∴ EC2=DB · AE
∵ DB=1cm,AE=4cm,
∴ EC=2cm.
∵ DE//BC,
∴DE:BC=AE:AC.
∴DE:5=4:6.
∴AC=AE+EC=6cm.
∴DE= cm.
解:
10
3
∴ ΔADE∽ΔABC.
4.如图,DE∥BC交AB于D,交AC于E,若AD:DB=2:3,BC=15,求DE的长.
A
D
B
E
C
∵ DE//BC,
DE
BC
∴
=
AD
AB
∵AD:DB=2:3,
∴AD:AB=2:5.
∴
DE
15
=
2
5
∴DE=6.
解:
∴ ΔADE∽ΔABC
练习巩固
5.如图,在□ABCD中,E是边BC上的一点,且
BE:EC=3:2,连接AE、BD交于点F,则
BE:AD=_____,BF:FD=_____.
A
B
C
D
E
F
3:5
3:5
∵BE:EC=3:2,
∴BE:BC=3:5.
∵ BC//AD,
∴BF:FD=BE:AD
=3:5.
∴BE:AD=3:5.
∵四边行ABCD是平行四边形
∴AD=BC.
∴ △BEF∽△DAF
6.如图,在△ABC中,∠C的平分线交AB于D,
过点D作DE∥BC交AC于E,若AD:DB=3:2,
则EC:BC=______.
A
B
C
E
D
3:5
1
2
3
∵CD平分∠ACB,
∵ DE//BC,
∴∠1 =∠2,
∴∠1 =∠3,
∴∠2 =∠3,
∴DE =EC,
∵AD:DB=3:2,
∴AD:AB=3:5.
∵ DE//BC,
∴EC:BC=AD:AB
=3:5.
∴ ΔADE∽ΔABC,
∴DE:BC=AD:AB,
课堂小结
3.用平行线法可证明哪类三角形相似?
1.相似三角形的定义怎样说?
2.相似三角形的相似比是指什么?
1.如图,在△ABC中,DE∥BC,AD=1,AB=4,则DE:BC=( ).
A. 1:2 B. 1:3
C. 2:3 D. 1:4
巩固提高
A
D
B
E
C
D
2.如图,点F在□ ABCD的边AB上,射线CF交DA的延长线于点E在不添加辅助线的情况下,与△ AEF相似的三角形有( ).
A. 0个 B. 1个
C. 2个 D. 3个
巩固提高
A
D
B
E
C
F
C
3.如图,在△ABC中,DE∥BC,AD:DB=
3:2,则AE:EC= ,DE:BC= .
A
D
B
E
C
3:2
3:5
4.如图,AD∥EF∥BC,则图中的相似三角形共有 对,分别是 .
A
D
B
E
C
F
3
△AEF∽△ABC
△BEF∽△BAD
△ADF∽△CBF
今天作业
课本P72页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.2相似三角形的判定(1)
用平行法判定三角形相似
教学目标
1.了解相似多边形的概念,掌握相似三角形及其相似比的概念;能用符号正确表示两个三角形相似;
2.会运用平行线法证明三角形相似.
教学重点:
用平行线法证明三角形相似.
教学难点:
用平行线法证明三角形相似.
相似多边形
各对应角相等、各对应边成的比相等的
多边形叫做相似多边形.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形的对应角相等,对应边的比相等.
学习新知
相似三角形
对应角相等、对应边成比例的三角形叫做相似三角形.
A
B
C
E
D
F
相似的表示方法
符号:∽ .
△ABC与△DEF相似
记作△ABC∽△DEF
注意:通常把对应顶点写在对应位置上. .
读作:相似于
学习新知
相似比
AB : A1B1 =
BC : B1C1 =
AC : A1C1
= k
时,
A
B
C
A1
B1
C1
则△ABC 与△A1B1C1 的相似比为 k .
或△A1B1C1 与△ABC 的相似比为 .
1
k
学习新知
如图,若点D是AB边上的任意一点, 过点D作DE∥BC,你能判定△ADE与△ABC相似吗?
A
B
C
D
E
∠A=∠A?
∠ADE=∠B?
∠AED=∠C?
AD
AB
=
AE
AC
=
DE
BC
?
探究新知
如图,在△ABC中,DE//BC,DE分别交AB,AC于点D,E . △ADE与△ABC有什么关系
A
B
C
D
E
解:
∵∠A= ∠A
∵ DE // BC,
∴∠1 =∠B,
∴ △ADE与△ABC的对应角相等.
△ADE与△ABC相似.
1
2
∠2 =∠C.
A
B
C
D
E
∵ DE // BC,
1
2
∴ 四边形DBFE是平行四边形.
∴ DE=BF .
∴ △ADE ∽ △ABC
过E作EF//AB交BC于F,
∴ △ADE与△ABC的对应边成比例.
∴ △ADE∽△ABC.
F
∵ DE // BC,
EF //AB,
AD
AB
∴
=
AE
AC
AE
AC
,
=
BF
BC
BF
BC
=
DE
BC
;
AD
AB
∴
=
AE
AC
=
DE
BC
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
A
B
C
D
E
∵ DE // BC,
∴ △ADE∽△ABC.
符号语言
探究新知
平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
定理可以适用以下三种情形:
∵DE∥BC
∴△ADE∽△ ABC
D
E
A
B
C
A
B
C
D
E
A
D
E
B
C
“8”字型
“A”字型
符号语言表示为:
A
B
C
D
E
相似具有传递性
△ADE∽△ABC
N
M
如果再作 MN∥DE ,共有多少对相似三角形?
△AMN∽△ADE
△AMN∽△ABC
共有三对相似三角形.
例1 如图, 已知DE∥BC,DF∥AC,请尽可能多地找出图中的相似三角形,并说明理由.
A
B
C
D
F
E
∵ DE∥BC
∵ DF∥AC
∴ ΔADE∽ΔDBF
∴ ΔDBF∽ΔABC
∴ ΔADE∽ΔABC
ΔADE∽ΔABC
∽ΔDBF
解:
例题解析
1.如图,在△ABC中,DE//BC,且AD=3,DB=2. 写出图中的相似三角形,并指出其相似比.
A
B
C
D
E
解:
∵ AD=3,
∴AB=AD+DB=3+2=5 ,
∴ △ADE与△ABC相似比为
△ADE与△ABC相似.
DB=2.
AD
AB
=
3
5
练习巩固
图中共有____对相似三角形.
2. 已知:如图,AB∥EF ∥CD,
3
△EOF∽△COD
AB∥EF
△AOB∽△FOE
AB∥CD
EF∥CD
△AOB ∽△DOC
3.如图,在△ABC中,DG∥EH∥FI∥BC,
(1)请找出图中所有的相似三角形;
(2)如果AD=1,DB=3,那么DG:BC=_____.
A
B
C
D
E
F
G
H
I
△ADG∽△AEH∽△AFI∽△ABC
1:4
∵ DG//BC,
∴DG:BC=AD:AB.
AB=AD+DB=1+3=4
∴ ΔADG∽ΔABC,
例2 如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.
A
B
C
D
E
[解析] 要求线段DE的长
要求AC的长
DE∥BC
要求EC的长
AE:EC=AD:DB.
例2 如图,在△ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的长.
A
B
C
D
E
∵ DE//BC,
∴AE:EC=AD:DB.
∵AD=EC,
∴AE:EC=EC:DB.
∴ EC2=DB · AE
∵ DB=1cm,AE=4cm,
∴ EC=2cm.
∵ DE//BC,
∴DE:BC=AE:AC.
∴DE:5=4:6.
∴AC=AE+EC=6cm.
∴DE= cm.
解:
10
3
∴ ΔADE∽ΔABC.
4.如图,DE∥BC交AB于D,交AC于E,若AD:DB=2:3,BC=15,求DE的长.
A
D
B
E
C
∵ DE//BC,
DE
BC
∴
=
AD
AB
∵AD:DB=2:3,
∴AD:AB=2:5.
∴
DE
15
=
2
5
∴DE=6.
解:
∴ ΔADE∽ΔABC
练习巩固
5.如图,在□ABCD中,E是边BC上的一点,且
BE:EC=3:2,连接AE、BD交于点F,则
BE:AD=_____,BF:FD=_____.
A
B
C
D
E
F
3:5
3:5
∵BE:EC=3:2,
∴BE:BC=3:5.
∵ BC//AD,
∴BF:FD=BE:AD
=3:5.
∴BE:AD=3:5.
∵四边行ABCD是平行四边形
∴AD=BC.
∴ △BEF∽△DAF
6.如图,在△ABC中,∠C的平分线交AB于D,
过点D作DE∥BC交AC于E,若AD:DB=3:2,
则EC:BC=______.
A
B
C
E
D
3:5
1
2
3
∵CD平分∠ACB,
∵ DE//BC,
∴∠1 =∠2,
∴∠1 =∠3,
∴∠2 =∠3,
∴DE =EC,
∵AD:DB=3:2,
∴AD:AB=3:5.
∵ DE//BC,
∴EC:BC=AD:AB
=3:5.
∴ ΔADE∽ΔABC,
∴DE:BC=AD:AB,
课堂小结
3.用平行线法可证明哪类三角形相似?
1.相似三角形的定义怎样说?
2.相似三角形的相似比是指什么?
1.如图,在△ABC中,DE∥BC,AD=1,AB=4,则DE:BC=( ).
A. 1:2 B. 1:3
C. 2:3 D. 1:4
巩固提高
A
D
B
E
C
D
2.如图,点F在□ ABCD的边AB上,射线CF交DA的延长线于点E在不添加辅助线的情况下,与△ AEF相似的三角形有( ).
A. 0个 B. 1个
C. 2个 D. 3个
巩固提高
A
D
B
E
C
F
C
3.如图,在△ABC中,DE∥BC,AD:DB=
3:2,则AE:EC= ,DE:BC= .
A
D
B
E
C
3:2
3:5
4.如图,AD∥EF∥BC,则图中的相似三角形共有 对,分别是 .
A
D
B
E
C
F
3
△AEF∽△ABC
△BEF∽△BAD
△ADF∽△CBF
今天作业
课本P72页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
