22.2相似三角形的判定(3) 课件(共29张PPT)
文档属性
| 名称 | 22.2相似三角形的判定(3) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 984.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
沪科版 九年级上册
22.2 相似三角形的判定(3)
用“两边对应成比例且夹角相等”判定三角形相似
教学目标:掌握两边对应成比例且夹角相等的方法证明三角形相似.
教学重点:
用两边对应成比例且夹角相等法证明三角形相似.
教学难点:
用两边对应成比例且夹角相等法证明三角形相似.
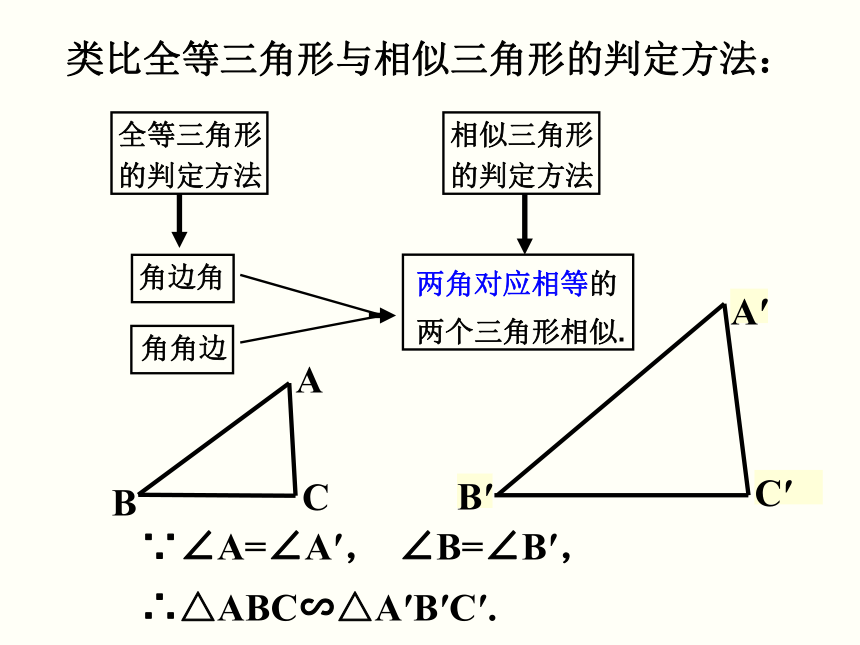
类比全等三角形与相似三角形的判定方法:
两角对应相等的
两个三角形相似.
角角边
角边角
全等三角形
的判定方法
相似三角形
的判定方法
A
B
C
B′
A′
C′
∵∠A=∠A′,
∠B=∠B′,
∴△ABC∽△A′B′C′.
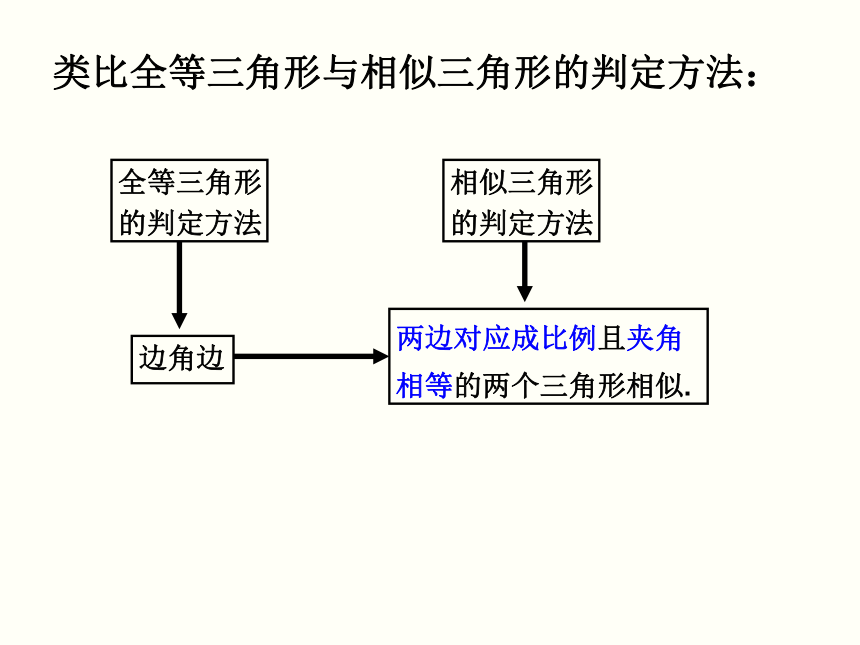
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
边角边
全等三角形
的判定方法
相似三角形
的判定方法
A
B
C
A′
C′
B′
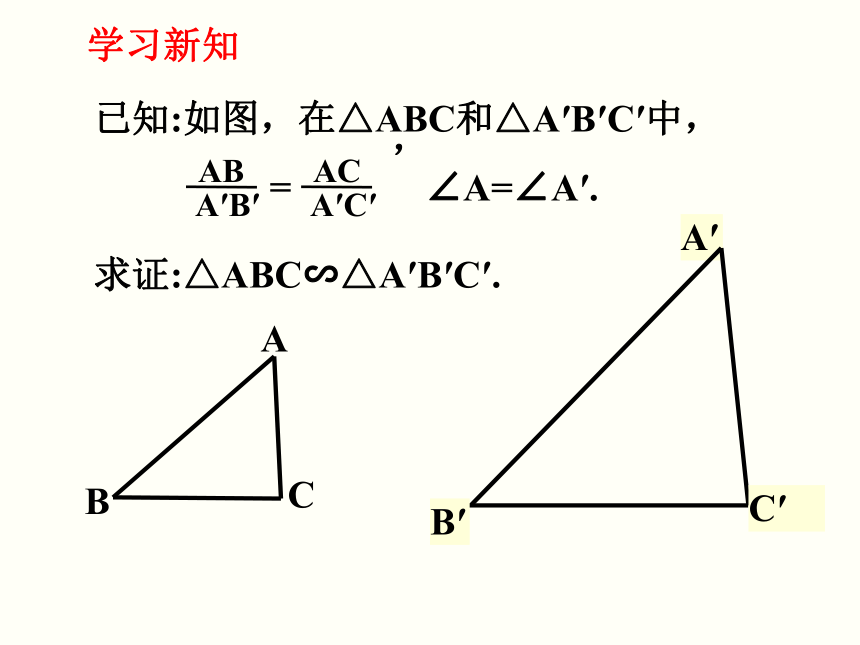
已知:如图,在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
=
AB
A′B′
AC
A′C′
,
∠A=∠A′.
学习新知
A
B
C
C′
B′
A′
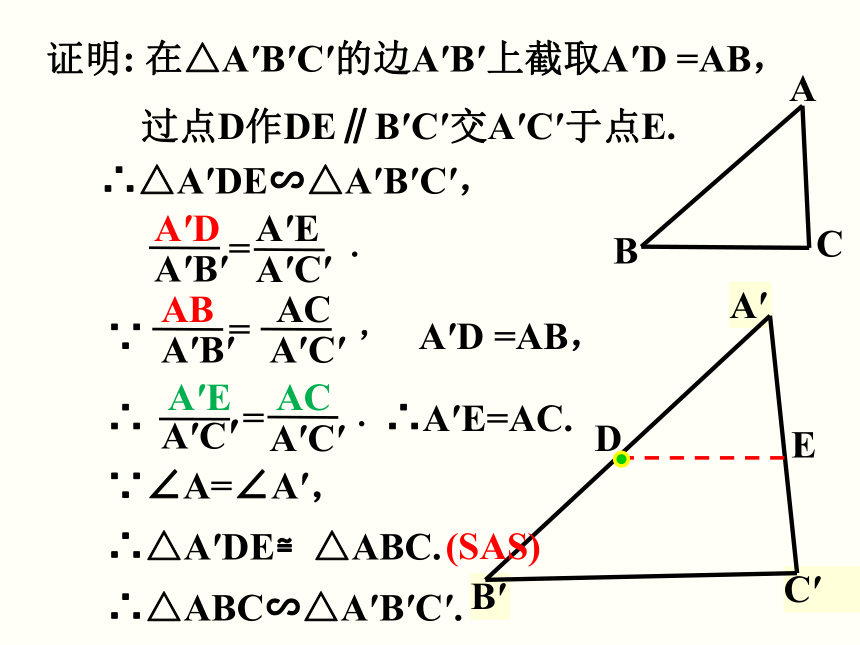
过点D作DE∥B′C′交A′C′于点E.
D
E
∴△A′DE∽△A′B′C′,
=
A′D
A′B′
A′E
A′C′
=
AB
A′B′
AC
A′C′
A′D =AB,
,
A′E
A′C′
=
AC
A′C′
∴A′E=AC.
∴△A′DE≌△ABC.
∴△ABC∽△A′B′C′.
∴
∵
.
.
∵∠A=∠A′,
证明: 在△A′B′C′的边A′B′上截取A′D =AB,
(SAS)
A
B
C
B′
A′
C′
=
AB
A′B′
AC
A′C′
△ABC∽△A′B′C′.
两边对应成比例且夹角相等的两个三角形相似.
∠A=∠A′,
∵ ,
∴
符号语言
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
理由如下:
AB
A′B′
∵
=
7
3
,
=
AC
A′C′
14
6
=
7
3
,
=
AB
A′B′
AC
A′C′
∴
∴△ABC∽△A′B′C′.
.
∠A=120°, AB=7cm, AC=14cm.
∠A′=120°, A′B′=3cm, A′C′=6cm.
∴∠A=∠A′,
解:△ABC∽△A′B′C′.
∵∠A=120°,∠A′=120°,
(教材P80)练习第1,2题
1. (1) 在△ABC中,∠A=48° ,AB=1.5cm, AC=2cm;在△DEF中, ∠E=48° , DE=2.8cm, EF=2.1cm. 问这两个三角形相似吗?为什么?
(2) 在△ABC中,∠A=120° , AB=7cm, AC=14cm;在△DEF中,∠D=120° ,DE=3cm,DF=6cm. 问这两个三角形相似吗?为什么?
练习巩固
理由如下:
AB
EF
∵
=
1.5
2.1
=
AC
DE
2
2.8
=
5
7
,
=
AB
EF
AC
DE
∴
∴△ABC∽△EFD.
.
∴∠A=∠E,
解:△ABC∽△EFD.
1. (1) 在△ABC中,∠A=48° ,AB=1.5cm, AC=2cm;在△DEF中, ∠E=48° , DE=2.8cm, EF=2.1cm. 问这两个三角形相似吗?为什么?
=
5
7
,
∵∠A=48°,∠E=48°,
理由如下:
AB
DE
∵
=
AC
DF
14
6
=
7
3
,
=
AB
DE
AC
DF
∴
∴△ABC∽△DEF.
.
∴∠A=∠D,
解:△ABC∽△DEF.
=
7
3
,
(2) 在△ABC中,∠A=120° , AB=7cm, AC=14cm;在△DEF中,∠D=120° ,DE=3cm,DF=6cm. 问这两个三角形相似吗?为什么?
∵∠A=120°,∠D=120°,
在Rt△ABC中, 两直角边分别为3cm, 4cm;
在Rt△A′B′C′中,斜边为25cm,一条直角边
为15cm.问这两个直角三角形相似吗?为什么?
A
B
C
A′
C′
B′
AC
A′C′
=
BC
B′C′
A′C′
解:
∵在Rt△ A′B′C′中,斜边A′B′=25cm,
一条直角边B′C′ =15cm,
∴A′C′2
=A′B′ 2-B′C′2
=25 2-152
=400
∴A′C′
=20
=
AC
A′C′
3
15
=
1
5
,
∴
=
BC
B′C′
4
20
=
1
5
,
这两个直角三角形相似,
理由如下:
AC
A′C′
=
BC
B′C′
∴
∴△ABC∽△A′B′C′.
∵∠C=∠C′,
A
B
C
A′
C′
B′
例2. 如图,BC与DE相交于点O.问:
(1) 当∠B满足什么条件时,△ABC∽△ADE?
(2) 当AC:AE满足什么条件时,△ABC∽△ADE?
D
B
A
C
E
O
解:(1)
∵∠A=∠A,
∴当∠B=∠D时,
△ABC∽△ADE.
(2)
∵∠A=∠A,
∴当AC:AE=AB:AD时,
△ABC∽△ADE.
A
B
C
D
E
例3 如图,△ABC中,D,E分别在AC,AB上,
且 ,BC=6,求DE的长.
=
AD
AB
AE
AC
=
1
2
解:
∵ ,
=
AD
AB
AE
AC
∠A=∠A,
∴△ADE∽△ABC.
∴
=
DE
BC
AE
AC
=
1
2
∵BC=6,
DE
6
=
1
2
∴DE=3.
∴
1.如图,一条直线分别交△ABC的边AB,AC于点D,E,下列条件中不能判定△ADE∽△ABC的是 ( )
A.∠ADE=∠B B.DE∥BC
D
A
B
C
D
E
C.
=
AD
AB
AE
AC
D.
=
AD
AB
DE
BC
练习巩固
2.判断图中△ABC和△EDC是否相似?
解:
∴△ABC∽△EDC.
∵∠1=∠2,
54
30
36
45
C
A
E
D
B
1
2
∵
=
BC
DC
45
30
=
3
2
,
=
BC
DC
∴
.
=
AC
EC
54
36
=
3
2
,
AC
EC
求证: DE‖BC.
A
B
C
D
E
3. 已知: 如图, 点D, E分别在AB, AC上,
=
AD
AB
AE
AC
,
证明:
∵ ,
=
AD
AB
AE
AC
∠A=∠A,
∴△ADE∽△ABC.
∴∠ADE=∠B,
∴DE‖BC.
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
两角对应相等的
两个三角形相似.
角边角
角角边
边角边
全等三角形
的判定方法
相似三角形
的判定方法
课堂小结
1.平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
2.两角分别相等的两三角形相似.
相似三角形的判定方法
3.两边对应成比例且夹角相等的两三角形相似.
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(1) 图中与△CDO相似的三角形有几个
(△CDO除外) ?请将它们写出来;
(2) 图中相似的非直角三角形有几对?
请将它们写出来;
(3) 选择(2)中的1对证明,
写出证明过程.
A
B
C
E
D
O
典型例析
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(1) 图中与△CDO相似的三角形有几个
(△CDO除外) ?请将它们写出来;
A
B
C
E
D
O
(1) 图中与△CDO相似的三角形有3个,
它们是:
△CEA,
△BEO,
△BDA.
解:
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(2) 图中相似的非直角三角形有几对?
请将它们写出来;
A
B
C
E
D
O
(2) 图中相似的非直角三角形有2对,
它们是:
△EOD∽△BOC,
△ADE∽△ABC.
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(3) 选择(2)中的1对证明,写出证明过程.
A
B
C
E
D
O
∴△EOD∽△BOC.
∵∠EOD=∠BOC,
证明:
∵∠BEO=∠CDO=90°,
∴△BEO∽△CDO.
∠BOE=∠COD,
∴BO:CO=EO:DO.
(3)求证: △EOD∽△BOC.
1. 如图,D是△ABC的边BC上一点,AB=2,BD=1,CD=3.求证: △ABD∽△CBA.
巩固提高
A
D
B
C
∴△ABD∽△CBA.
∵∠B=∠B,
∴BD:BA=AB:CB.
∵AB=2,BD=1,
∴BD:BA=1:2.
∵ BD=1,CD=3,
证明:
∴BD+CD=1+3=4=CB.
∴AB:CB=2:4=1:2.
2. 如图,在等腰△ABC中,AB=AC=12,BC=8,BD=3,CE=2.求证: △ABD∽△BCE.
A
D
B
C
∴△ABD∽△BCE.
∴∠ABD=∠BCE,
∴BD:AB=CE:BC.
∵AB=12,BD=3,
∴BD:AB=3:12=1:4.
∵ CE=2,BC=8,
证明:
∴CE:BC=2:8=1:1.
E
∵AB =AC
今天作业
课本P85页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.2 相似三角形的判定(3)
用“两边对应成比例且夹角相等”判定三角形相似
教学目标:掌握两边对应成比例且夹角相等的方法证明三角形相似.
教学重点:
用两边对应成比例且夹角相等法证明三角形相似.
教学难点:
用两边对应成比例且夹角相等法证明三角形相似.
类比全等三角形与相似三角形的判定方法:
两角对应相等的
两个三角形相似.
角角边
角边角
全等三角形
的判定方法
相似三角形
的判定方法
A
B
C
B′
A′
C′
∵∠A=∠A′,
∠B=∠B′,
∴△ABC∽△A′B′C′.
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
边角边
全等三角形
的判定方法
相似三角形
的判定方法
A
B
C
A′
C′
B′
已知:如图,在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
=
AB
A′B′
AC
A′C′
,
∠A=∠A′.
学习新知
A
B
C
C′
B′
A′
过点D作DE∥B′C′交A′C′于点E.
D
E
∴△A′DE∽△A′B′C′,
=
A′D
A′B′
A′E
A′C′
=
AB
A′B′
AC
A′C′
A′D =AB,
,
A′E
A′C′
=
AC
A′C′
∴A′E=AC.
∴△A′DE≌△ABC.
∴△ABC∽△A′B′C′.
∴
∵
.
.
∵∠A=∠A′,
证明: 在△A′B′C′的边A′B′上截取A′D =AB,
(SAS)
A
B
C
B′
A′
C′
=
AB
A′B′
AC
A′C′
△ABC∽△A′B′C′.
两边对应成比例且夹角相等的两个三角形相似.
∠A=∠A′,
∵ ,
∴
符号语言
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
理由如下:
AB
A′B′
∵
=
7
3
,
=
AC
A′C′
14
6
=
7
3
,
=
AB
A′B′
AC
A′C′
∴
∴△ABC∽△A′B′C′.
.
∠A=120°, AB=7cm, AC=14cm.
∠A′=120°, A′B′=3cm, A′C′=6cm.
∴∠A=∠A′,
解:△ABC∽△A′B′C′.
∵∠A=120°,∠A′=120°,
(教材P80)练习第1,2题
1. (1) 在△ABC中,∠A=48° ,AB=1.5cm, AC=2cm;在△DEF中, ∠E=48° , DE=2.8cm, EF=2.1cm. 问这两个三角形相似吗?为什么?
(2) 在△ABC中,∠A=120° , AB=7cm, AC=14cm;在△DEF中,∠D=120° ,DE=3cm,DF=6cm. 问这两个三角形相似吗?为什么?
练习巩固
理由如下:
AB
EF
∵
=
1.5
2.1
=
AC
DE
2
2.8
=
5
7
,
=
AB
EF
AC
DE
∴
∴△ABC∽△EFD.
.
∴∠A=∠E,
解:△ABC∽△EFD.
1. (1) 在△ABC中,∠A=48° ,AB=1.5cm, AC=2cm;在△DEF中, ∠E=48° , DE=2.8cm, EF=2.1cm. 问这两个三角形相似吗?为什么?
=
5
7
,
∵∠A=48°,∠E=48°,
理由如下:
AB
DE
∵
=
AC
DF
14
6
=
7
3
,
=
AB
DE
AC
DF
∴
∴△ABC∽△DEF.
.
∴∠A=∠D,
解:△ABC∽△DEF.
=
7
3
,
(2) 在△ABC中,∠A=120° , AB=7cm, AC=14cm;在△DEF中,∠D=120° ,DE=3cm,DF=6cm. 问这两个三角形相似吗?为什么?
∵∠A=120°,∠D=120°,
在Rt△ABC中, 两直角边分别为3cm, 4cm;
在Rt△A′B′C′中,斜边为25cm,一条直角边
为15cm.问这两个直角三角形相似吗?为什么?
A
B
C
A′
C′
B′
AC
A′C′
=
BC
B′C′
A′C′
解:
∵在Rt△ A′B′C′中,斜边A′B′=25cm,
一条直角边B′C′ =15cm,
∴A′C′2
=A′B′ 2-B′C′2
=25 2-152
=400
∴A′C′
=20
=
AC
A′C′
3
15
=
1
5
,
∴
=
BC
B′C′
4
20
=
1
5
,
这两个直角三角形相似,
理由如下:
AC
A′C′
=
BC
B′C′
∴
∴△ABC∽△A′B′C′.
∵∠C=∠C′,
A
B
C
A′
C′
B′
例2. 如图,BC与DE相交于点O.问:
(1) 当∠B满足什么条件时,△ABC∽△ADE?
(2) 当AC:AE满足什么条件时,△ABC∽△ADE?
D
B
A
C
E
O
解:(1)
∵∠A=∠A,
∴当∠B=∠D时,
△ABC∽△ADE.
(2)
∵∠A=∠A,
∴当AC:AE=AB:AD时,
△ABC∽△ADE.
A
B
C
D
E
例3 如图,△ABC中,D,E分别在AC,AB上,
且 ,BC=6,求DE的长.
=
AD
AB
AE
AC
=
1
2
解:
∵ ,
=
AD
AB
AE
AC
∠A=∠A,
∴△ADE∽△ABC.
∴
=
DE
BC
AE
AC
=
1
2
∵BC=6,
DE
6
=
1
2
∴DE=3.
∴
1.如图,一条直线分别交△ABC的边AB,AC于点D,E,下列条件中不能判定△ADE∽△ABC的是 ( )
A.∠ADE=∠B B.DE∥BC
D
A
B
C
D
E
C.
=
AD
AB
AE
AC
D.
=
AD
AB
DE
BC
练习巩固
2.判断图中△ABC和△EDC是否相似?
解:
∴△ABC∽△EDC.
∵∠1=∠2,
54
30
36
45
C
A
E
D
B
1
2
∵
=
BC
DC
45
30
=
3
2
,
=
BC
DC
∴
.
=
AC
EC
54
36
=
3
2
,
AC
EC
求证: DE‖BC.
A
B
C
D
E
3. 已知: 如图, 点D, E分别在AB, AC上,
=
AD
AB
AE
AC
,
证明:
∵ ,
=
AD
AB
AE
AC
∠A=∠A,
∴△ADE∽△ABC.
∴∠ADE=∠B,
∴DE‖BC.
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
两角对应相等的
两个三角形相似.
角边角
角角边
边角边
全等三角形
的判定方法
相似三角形
的判定方法
课堂小结
1.平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
2.两角分别相等的两三角形相似.
相似三角形的判定方法
3.两边对应成比例且夹角相等的两三角形相似.
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(1) 图中与△CDO相似的三角形有几个
(△CDO除外) ?请将它们写出来;
(2) 图中相似的非直角三角形有几对?
请将它们写出来;
(3) 选择(2)中的1对证明,
写出证明过程.
A
B
C
E
D
O
典型例析
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(1) 图中与△CDO相似的三角形有几个
(△CDO除外) ?请将它们写出来;
A
B
C
E
D
O
(1) 图中与△CDO相似的三角形有3个,
它们是:
△CEA,
△BEO,
△BDA.
解:
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(2) 图中相似的非直角三角形有几对?
请将它们写出来;
A
B
C
E
D
O
(2) 图中相似的非直角三角形有2对,
它们是:
△EOD∽△BOC,
△ADE∽△ABC.
例4. 如图,△ABC的边AC,AB上的高线BD,CE相交于点O,连接DE.
(3) 选择(2)中的1对证明,写出证明过程.
A
B
C
E
D
O
∴△EOD∽△BOC.
∵∠EOD=∠BOC,
证明:
∵∠BEO=∠CDO=90°,
∴△BEO∽△CDO.
∠BOE=∠COD,
∴BO:CO=EO:DO.
(3)求证: △EOD∽△BOC.
1. 如图,D是△ABC的边BC上一点,AB=2,BD=1,CD=3.求证: △ABD∽△CBA.
巩固提高
A
D
B
C
∴△ABD∽△CBA.
∵∠B=∠B,
∴BD:BA=AB:CB.
∵AB=2,BD=1,
∴BD:BA=1:2.
∵ BD=1,CD=3,
证明:
∴BD+CD=1+3=4=CB.
∴AB:CB=2:4=1:2.
2. 如图,在等腰△ABC中,AB=AC=12,BC=8,BD=3,CE=2.求证: △ABD∽△BCE.
A
D
B
C
∴△ABD∽△BCE.
∴∠ABD=∠BCE,
∴BD:AB=CE:BC.
∵AB=12,BD=3,
∴BD:AB=3:12=1:4.
∵ CE=2,BC=8,
证明:
∴CE:BC=2:8=1:1.
E
∵AB =AC
今天作业
课本P85页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
