22.2 相似三角形的判定(4)课件(共24张PPT)
文档属性
| 名称 | 22.2 相似三角形的判定(4)课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 975.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 13:54:26 | ||
图片预览




文档简介
(共24张PPT)
沪科版 九年级上册
22.2 相似三角形的判定(4)
用“三边对应成比例”判定三角形相似
教学目标:掌握三边成比例的方法证明三角形相似.
教学重点:
用三边对应成比例法证明三角形相似.
教学难点:
用三边对应成比例等法证明三角形相似.
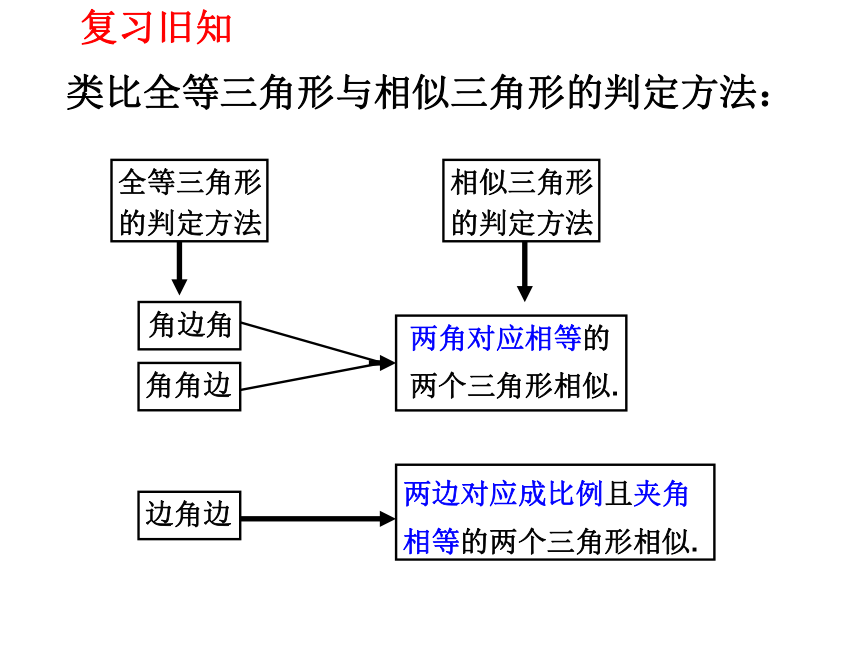
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
两角对应相等的
两个三角形相似.
角边角
角角边
边角边
全等三角形
的判定方法
相似三角形
的判定方法
复习旧知
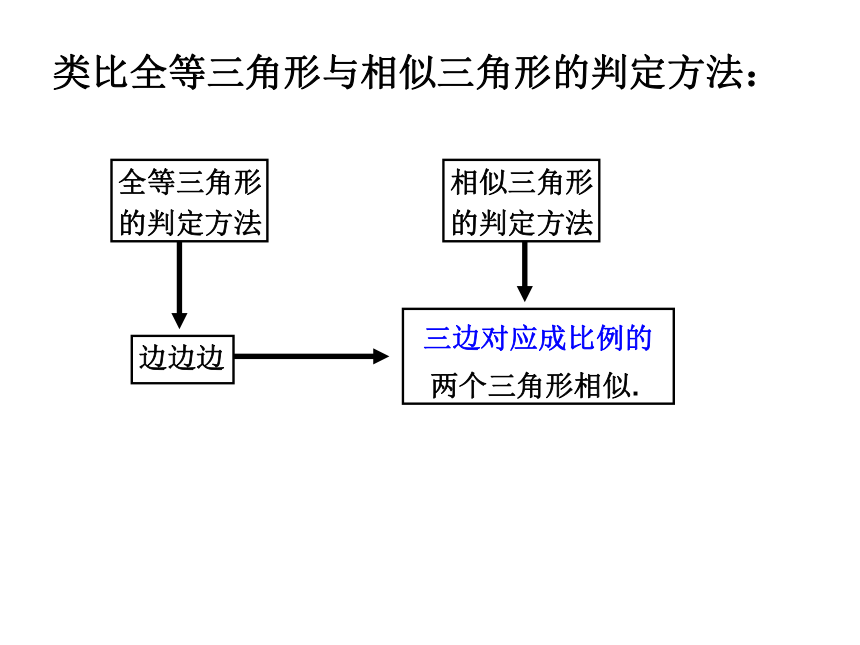
类比全等三角形与相似三角形的判定方法:
三边对应成比例的
两个三角形相似.
边边边
全等三角形
的判定方法
相似三角形
的判定方法
A′
C′
B′
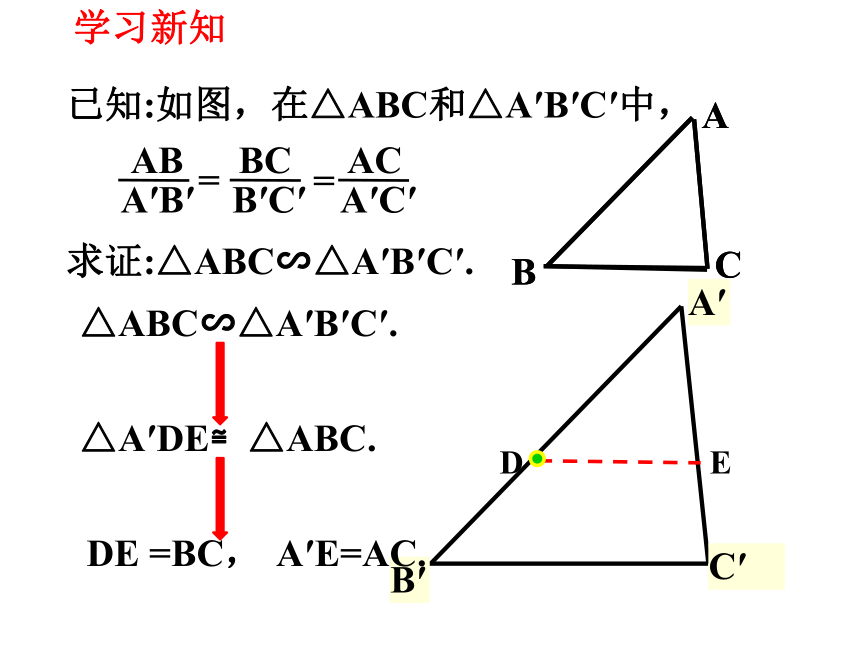
已知:如图,在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
A
B
C
A
B
C
DE =BC,
A′E=AC.
△A′DE≌△ABC.
△ABC∽△A′B′C′.
D
E
=
=
AB
A′B′
BC
B′C′
AC
A′C′
学习新知
A
B
C
C′
B′
A′
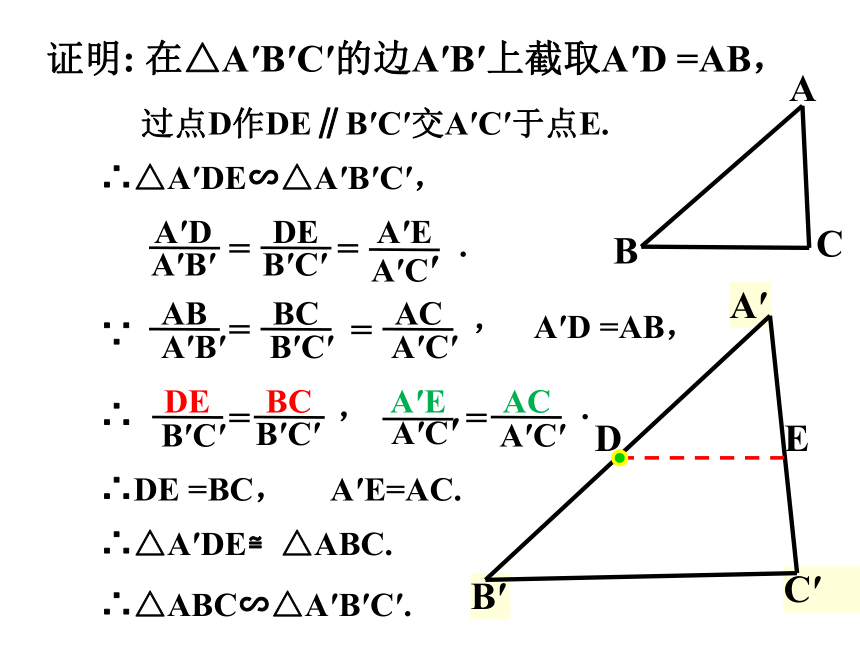
过点D作DE∥B′C′交A′C′于点E.
D
E
∴△A′DE∽△A′B′C′,
=
=
A′D
A′B′
DE
B′C′
A′E
A′C′
=
=
AB
A′B′
BC
B′C′
AC
A′C′
A′D =AB,
,
DE
B′C′
=
BC
B′C′
A′E
A′C′
=
AC
A′C′
∴DE =BC,
A′E=AC.
∴△A′DE≌△ABC.
∴△ABC∽△A′B′C′.
∴
∵
.
,
.
证明: 在△A′B′C′的边A′B′上截取A′D =AB,
A
B
C
A′
C′
B′
=
=
AB
A′B′
BC
B′C′
AC
A′C′
∴△ABC∽△A′B′C′.
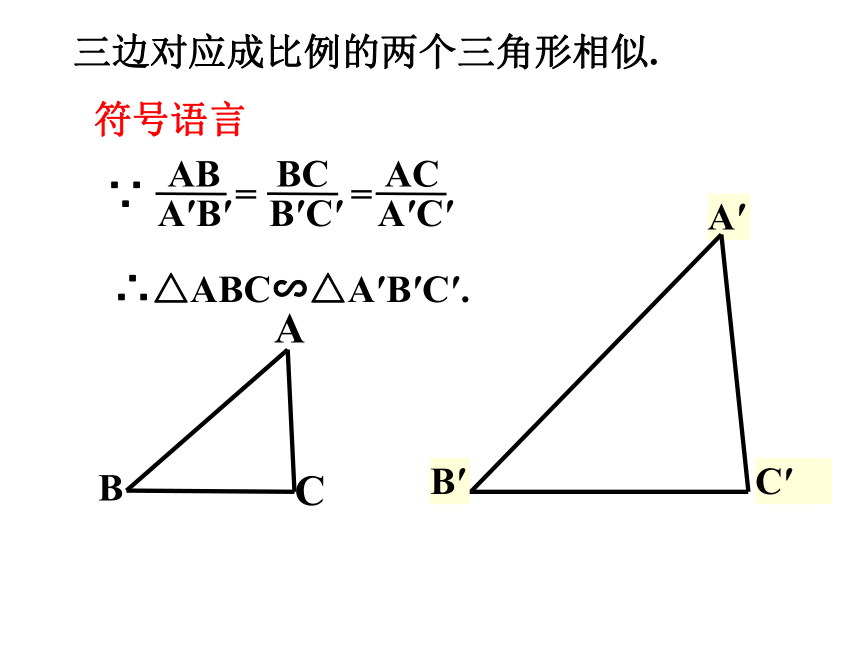
三边对应成比例的两个三角形相似.
∵
符号语言
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=4 , BC=6, AC=8,
A′B′=12, B′C′=18, A′C′=24.
(2) AB=2, BC= , AC= ,
A′B′= , B′C′=1, A′C′= .
2
10
2
5
例题解析
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=4 , BC=6, AC=8,
A′B′=12, B′C′=18, A′C′=24.
解:(1)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
4
12
∵
=
1
3
,
=
BC
B′C′
6
18
=
1
3
,
=
AC
A′C′
8
24
=
1
3
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
解:(2)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
2
∵
=
BC
B′C′
1
=
AC
A′C′
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
1. 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(2) AB=2, BC= , AC= ,
A′B′= , B′C′=1, A′C′= .
2
10
2
5
=
,
2
2
=
,
2
2
=
,
2
10
5
1 . 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=10, BC=8, AC=16,
A′B′=16, B′C′=12.8, A′C′=25.6.
(2) AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
练习巩固
解:(1)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
10
16
∵
=
5
8
,
=
BC
B′C′
8
12.8
=
5
8
,
=
AC
A′C′
16
25.6
=
5
8
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
1. 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=10, BC=8, AC=16,
A′B′=16, B′C′=12.8, A′C′=25.6.
解:(2)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
8
12
∵
=
2
3
,
=
BC
B′C′
12
18
=
2
3
,
=
AC
A′C′
18
27
=
2
3
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
(2) AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
1 . 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
理解对应的意义.
B
A
C
A′
B′
C′
例2. 如图,方格网的小方格是边长为1的正方形, △ABC与△A′B′C′ 的顶点都在格点上,判断△ABC与△A′B′C′ 是否相似, 为什么?
∵△ABC与△A′B′C′ 的顶点都在格点上,
∴AB= = ,
A′B′= = ,
解:(2)△ABC∽△A′B′C′.
理由如下:
12+12
2
AC=2,
BC= = ,
12+32
10
12+22
5
A′C′= = ,
12+32
10
B′C′=5.
A′B′= = ,A′C′= = ,B′C′=5 .
B
A
C
A′
B′
C′
∵△ABC与△A′B′C′ 的顶点都在格点上,
∴AB= = ,AC=2,BC= = ,
解:△ABC∽△A′B′C′.
理由如下:
2
12+12
12+32
10
12+22
5
12+32
10
∴
=
AB
A′B′
5
=
,
2
5
10
=
AC
A′C′
2
10
5
10
=
=
BC
B′C′
5
10
∴
∴
△ABC∽△A′B′C′.
=
=
AB
A′B′
AC
A′C′
BC
B′C′
=
=
8
4
10
x
12
y
解:
=
=
8
x
10
4
12
y
=
=
8
x
10
y
12
4
当 时,
当 时,
当 时,
x=5,
y=6.
x=3.2,
y=4.8.
x= ,
y= .
8
3
10
3
画法不唯一,有三种画法.
3. 要画两个相似三角形,其中一个三角形的三边长分别为8,10,12,另一个三角形的一边长是4,求另一个三角形的其余两边长.你画的三角形唯一吗?
练习巩固
4. 顺次连接三角形三边中点所得的小三角形与原三角形相似吗?为什么?
答: 顺次连接三角形三边中点所得的小三角形与原三角形相似.
A
B
C
D
E
F
因小三角形与原三角形相似
三对应边的比都是1:2,即三边对应成比例,所以它们相似.
1.平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
2.两角分别相等的两三角形相似.
相似三角形的判定方法
3.两边对应成比例且夹角相等的两三角形相似.
课堂小结
4.三边对应成比例的两三角形相似.
如图,AE=4cm, AD=3cm, DE=2.4cm, BD=2cm,CE= cm, 求BC的长.
A
B
C
D
E
8
3
△ADE∽△ABC
BC=?
分析:
=
AD
AB
AE
AC
AB
AC
典型例析
如图,AE=4cm, AD=3cm, DE=2.4cm, BD=2cm,CE= cm, 求BC的长.
A
B
C
D
E
8
3
∵AE=4,AD=3,BD=2,CE= ,
∴AB=AD+BD=3+2=5,
AC=AE+EC=4+ = ,
8
3
20
3
∴AD:AB=3:5,
AE:AC=4:
8
3
20
3
=3:5.
∴AD:AB=AE:AC.
∵∠A=∠A,
∴△ADE∽△ABC.
∴DE:BC=AE:AB.
∴2.4:BC=3:5.
∴BC=4(cm).
解:
如图,在△ABC中,AD=2BD,AE=2CE, DE:BC=2:3 .求证: △ADE∽△ABC.
巩固提高
∴△ABD∽△CBA.
∵AD=2BD,
∵ DE:BC=2:3,
证明:
∴AB=AD+BD=3BD,
∴AD:AB=2:3,
AE=2CE,
AC=AE+CE=3CE.
AE:AC=2:3.
∴AD:AB=AE:AC=DE:BC
A
D
B
C
E
今天作业
课本P86页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.2 相似三角形的判定(4)
用“三边对应成比例”判定三角形相似
教学目标:掌握三边成比例的方法证明三角形相似.
教学重点:
用三边对应成比例法证明三角形相似.
教学难点:
用三边对应成比例等法证明三角形相似.
类比全等三角形与相似三角形的判定方法:
两边对应成比例且夹角
相等的两个三角形相似.
两角对应相等的
两个三角形相似.
角边角
角角边
边角边
全等三角形
的判定方法
相似三角形
的判定方法
复习旧知
类比全等三角形与相似三角形的判定方法:
三边对应成比例的
两个三角形相似.
边边边
全等三角形
的判定方法
相似三角形
的判定方法
A′
C′
B′
已知:如图,在△ABC和△A′B′C′中,
求证:△ABC∽△A′B′C′.
A
B
C
A
B
C
DE =BC,
A′E=AC.
△A′DE≌△ABC.
△ABC∽△A′B′C′.
D
E
=
=
AB
A′B′
BC
B′C′
AC
A′C′
学习新知
A
B
C
C′
B′
A′
过点D作DE∥B′C′交A′C′于点E.
D
E
∴△A′DE∽△A′B′C′,
=
=
A′D
A′B′
DE
B′C′
A′E
A′C′
=
=
AB
A′B′
BC
B′C′
AC
A′C′
A′D =AB,
,
DE
B′C′
=
BC
B′C′
A′E
A′C′
=
AC
A′C′
∴DE =BC,
A′E=AC.
∴△A′DE≌△ABC.
∴△ABC∽△A′B′C′.
∴
∵
.
,
.
证明: 在△A′B′C′的边A′B′上截取A′D =AB,
A
B
C
A′
C′
B′
=
=
AB
A′B′
BC
B′C′
AC
A′C′
∴△ABC∽△A′B′C′.
三边对应成比例的两个三角形相似.
∵
符号语言
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=4 , BC=6, AC=8,
A′B′=12, B′C′=18, A′C′=24.
(2) AB=2, BC= , AC= ,
A′B′= , B′C′=1, A′C′= .
2
10
2
5
例题解析
例1 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=4 , BC=6, AC=8,
A′B′=12, B′C′=18, A′C′=24.
解:(1)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
4
12
∵
=
1
3
,
=
BC
B′C′
6
18
=
1
3
,
=
AC
A′C′
8
24
=
1
3
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
解:(2)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
2
∵
=
BC
B′C′
1
=
AC
A′C′
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
1. 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(2) AB=2, BC= , AC= ,
A′B′= , B′C′=1, A′C′= .
2
10
2
5
=
,
2
2
=
,
2
2
=
,
2
10
5
1 . 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=10, BC=8, AC=16,
A′B′=16, B′C′=12.8, A′C′=25.6.
(2) AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
练习巩固
解:(1)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
10
16
∵
=
5
8
,
=
BC
B′C′
8
12.8
=
5
8
,
=
AC
A′C′
16
25.6
=
5
8
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
1. 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1) AB=10, BC=8, AC=16,
A′B′=16, B′C′=12.8, A′C′=25.6.
解:(2)△ABC∽△A′B′C′.
理由如下:
=
AB
A′B′
8
12
∵
=
2
3
,
=
BC
B′C′
12
18
=
2
3
,
=
AC
A′C′
18
27
=
2
3
,
∴
∴
△ABC∽△A′B′C′.
.
=
=
AB
A′B′
BC
B′C′
AC
A′C′
(2) AB=8 , BC=12 , AC=18
A′B′=12 , B′C′=18 , A′C′=27
1 . 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
理解对应的意义.
B
A
C
A′
B′
C′
例2. 如图,方格网的小方格是边长为1的正方形, △ABC与△A′B′C′ 的顶点都在格点上,判断△ABC与△A′B′C′ 是否相似, 为什么?
∵△ABC与△A′B′C′ 的顶点都在格点上,
∴AB= = ,
A′B′= = ,
解:(2)△ABC∽△A′B′C′.
理由如下:
12+12
2
AC=2,
BC= = ,
12+32
10
12+22
5
A′C′= = ,
12+32
10
B′C′=5.
A′B′= = ,A′C′= = ,B′C′=5 .
B
A
C
A′
B′
C′
∵△ABC与△A′B′C′ 的顶点都在格点上,
∴AB= = ,AC=2,BC= = ,
解:△ABC∽△A′B′C′.
理由如下:
2
12+12
12+32
10
12+22
5
12+32
10
∴
=
AB
A′B′
5
=
,
2
5
10
=
AC
A′C′
2
10
5
10
=
=
BC
B′C′
5
10
∴
∴
△ABC∽△A′B′C′.
=
=
AB
A′B′
AC
A′C′
BC
B′C′
=
=
8
4
10
x
12
y
解:
=
=
8
x
10
4
12
y
=
=
8
x
10
y
12
4
当 时,
当 时,
当 时,
x=5,
y=6.
x=3.2,
y=4.8.
x= ,
y= .
8
3
10
3
画法不唯一,有三种画法.
3. 要画两个相似三角形,其中一个三角形的三边长分别为8,10,12,另一个三角形的一边长是4,求另一个三角形的其余两边长.你画的三角形唯一吗?
练习巩固
4. 顺次连接三角形三边中点所得的小三角形与原三角形相似吗?为什么?
答: 顺次连接三角形三边中点所得的小三角形与原三角形相似.
A
B
C
D
E
F
因小三角形与原三角形相似
三对应边的比都是1:2,即三边对应成比例,所以它们相似.
1.平行于三角形一边的直线与其他两边相交,
所构成的三角形与原三角形相似.
2.两角分别相等的两三角形相似.
相似三角形的判定方法
3.两边对应成比例且夹角相等的两三角形相似.
课堂小结
4.三边对应成比例的两三角形相似.
如图,AE=4cm, AD=3cm, DE=2.4cm, BD=2cm,CE= cm, 求BC的长.
A
B
C
D
E
8
3
△ADE∽△ABC
BC=?
分析:
=
AD
AB
AE
AC
AB
AC
典型例析
如图,AE=4cm, AD=3cm, DE=2.4cm, BD=2cm,CE= cm, 求BC的长.
A
B
C
D
E
8
3
∵AE=4,AD=3,BD=2,CE= ,
∴AB=AD+BD=3+2=5,
AC=AE+EC=4+ = ,
8
3
20
3
∴AD:AB=3:5,
AE:AC=4:
8
3
20
3
=3:5.
∴AD:AB=AE:AC.
∵∠A=∠A,
∴△ADE∽△ABC.
∴DE:BC=AE:AB.
∴2.4:BC=3:5.
∴BC=4(cm).
解:
如图,在△ABC中,AD=2BD,AE=2CE, DE:BC=2:3 .求证: △ADE∽△ABC.
巩固提高
∴△ABD∽△CBA.
∵AD=2BD,
∵ DE:BC=2:3,
证明:
∴AB=AD+BD=3BD,
∴AD:AB=2:3,
AE=2CE,
AC=AE+CE=3CE.
AE:AC=2:3.
∴AD:AB=AE:AC=DE:BC
A
D
B
C
E
今天作业
课本P86页第7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
