22.3 相似三角形的性质(2)课件(共25张PPT)
文档属性
| 名称 | 22.3 相似三角形的性质(2)课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 13:56:10 | ||
图片预览








文档简介
(共25张PPT)
沪科版 九年级上册
22.3相似三角形的性质(2)
教学目标:会利用相似三角形的性质解决简单的实
际问题.
教学重点:
用相似三角形对应的高的比的性质解题.
教学难点:
用相似三角形高的比的性质解题.
(2)相似三角形对应的 高、中线、角平分线
的比等于相似比.
相似三角形的性质:
(4)相似三角形面积的比等于相似比的平方.
(3)相似三角形周长的比等于相似比.
相似三角形的相似比等于面积比的算术平方根.
(1)相似三角形对应角相等,对应边成比例.
(1)已知 △ABC∽△A′B′C′,的相似比为2:1,
则周长比为 ,对应边上中线之比 ,
面积之比为 .
2:1
4:1
2:1
温故知新
(2)已知△ABC∽△A′B′C′,且面积之比为1:9,
则相似比为 ,对应边上的高线之比为 ,周长之比为 .
1:3
1:3
1:3
(4)若两个相似三角形的面积比是3:4,
那么这两个三角形的周长比是_______.
(3)两个相似三角形的周长分别是10和40,
那么这两个三角形的面积比是______.
1:16
:2
3
(5)两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是120cm2 ,则较小三角形的周长___cm,面积为 cm2.
6:18=1:3
1:3=x:42
3x=42
x=14
14
1:9=y:120
y=
40
3
40
3
P
Q
S
R
A
B
C
D
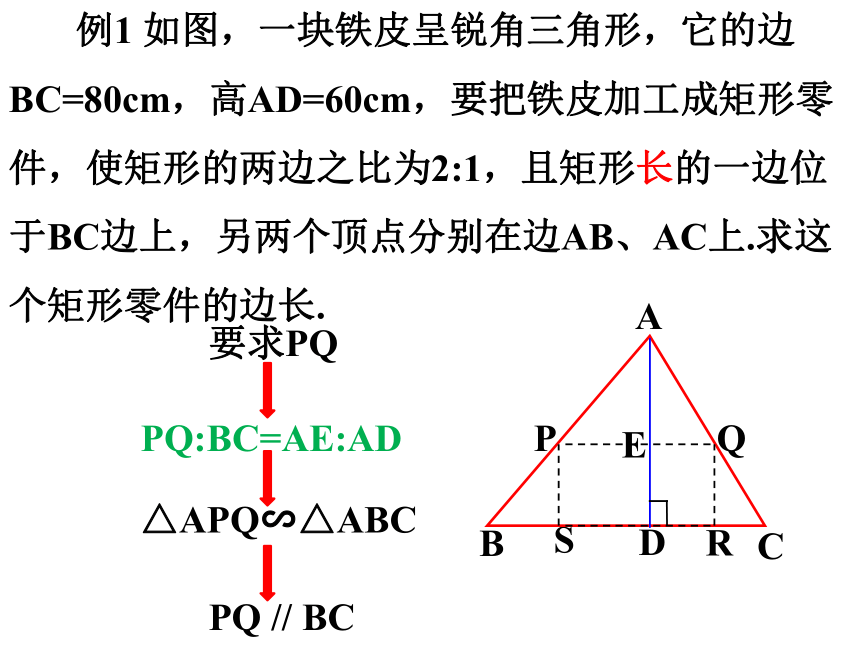
例1 如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形长的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
E
要求PQ
△APQ∽△ABC
PQ // BC
PQ:BC=AE:AD
∴ ,
P
Q
S
R
A
B
C
D
E
解:如图,矩形PQRS为加工后的矩形零件,
长边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PS为xcm,则PQ为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为48cm和 24cm.
PQ
BC
AE
AD
=
x=24,
2x=48.
∴ ,
2x
80
60-x
60
=
∴ 6x=4(60-x),
AE=
AD-ED
=AD-PS
=(60-x)cm.
6x=240-4x
A
B
C
D
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
例1 如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形长的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
A
B
C
D
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
方案(1)矩形长的一边位于边BC上.
方案(2)矩形短的一边位于边BC上.
A
B
C
D
方案(2)矩形短的一边位于边BC上.
P
Q
S
R
A
B
C
D
P
Q
S
R
方案(1)矩形长的一边位于边BC上.
∴ ,
P
Q
S
R
A
B
C
D
E
解:①如图,矩形PQRS为加工后的矩形零件,
长边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PS为xcm,则PQ为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为48cm和 24cm.
PQ
BC
AE
AD
=
x=24,
2x=48.
∴ ,
2x
80
60-x
60
=
∴ 6x=4(60-x),
AE=
AD-ED
=AD-PS
=(60-x)cm.
6x=240-4x
∴ ,
P
Q
S
R
A
B
C
D
E
解:②如图,矩形PQRS为加工后的矩形零件,
短边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PQ为xcm,则PS为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为 cm和 cm.
PQ
BC
AE
AD
=
x= ,
2x= .
∴ ,
x
80
60-2x
60
=
∴ 6x=8(60-2x),
AE=
AD-ED
=AD-PS
=(60-2x)cm.
3x=240-8x
240
11
480
11
240
11
480
11
A
B
C
D
2.已知,在△ABC中,BC=120mm,边BC上的高为80mm,在这个三角形内有一个内接矩形,矩形的一边在BC边上,另两个顶点分别在边AB,AC上.问当这个矩形面积最大时,它的边长各是多少?
P
Q
S
R
E
S矩形PQRS
=PQ · PS
=x · y
∴ ,
P
Q
S
R
A
B
C
D
E
解:如图,
设矩形PQRS的边PQ为xmm,PS
为ymm;
∵ PQ//BC,
∴△APQ∽△ABC,
PQ
BC
AE
AD
=
∴ ,
x
120
80-y
80
=
∴ y=80- x,
则AE=
AD-ED
=AD-PS
=(80-y)mm.
2
3
∵ S矩形PQRS
=PQ · PS
=x · y
∴ S矩形PQRS
=x · (80- x)
2
3
解:如图,
设矩形PQRS的边PQ为xmm,PS
为ymm;
∵ PQ//BC,
∴△APQ∽△ABC,
PQ
BC
AE
AD
=
∴ ,
∴ ,
x
120
80-y
80
=
∴ y=80- x,
则AE=
AD-ED
=AD-PS
=(80-y)mm.
2
3
∵ S矩形PQRS
=PQ · PS
=x · y
∴ S矩形PQRS
=x · (80- x)
2
3
= - x2 + 80x
2
3
∵- <0,
∴ S矩形PQRS有最大值,
2
3
此时,
x=
80
2 · (- )
2
3
-
=60(mm),
∴ y=40mm.
有相似三角形,又有垂直,就有 高的比等于 相似比.充分挖掘题目中隐含的条件、利用相似三角形对应线段的比等于相似比列方程是解题的关键.
解题心得
1.已知相似三角形面积的比为9∶4,那么这两个三角形的周长之比为( ).
A.9∶4 B.4∶9
C.3∶2 D.81∶16
C
巩固提高
2.己知两个相似三角形周长的比为3:2,
其中较小的三角形面积为12,则较大的
三角形的面积是( ).
A.27 B.24 C.18 D.16
A
A
B
C
D
3.如图,一块铁皮呈锐角三角形,它的边BC=120cm,高AD=80cm,要把铁皮加工成正方形零件,使正方形的一边GH位于BC边上,另两个顶点E、F分别在边AB、AC上.则这个正方形零件的边长为 cm.
E
F
G
H
48
今天作业
课本P90页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.3相似三角形的性质(2)
教学目标:会利用相似三角形的性质解决简单的实
际问题.
教学重点:
用相似三角形对应的高的比的性质解题.
教学难点:
用相似三角形高的比的性质解题.
(2)相似三角形对应的 高、中线、角平分线
的比等于相似比.
相似三角形的性质:
(4)相似三角形面积的比等于相似比的平方.
(3)相似三角形周长的比等于相似比.
相似三角形的相似比等于面积比的算术平方根.
(1)相似三角形对应角相等,对应边成比例.
(1)已知 △ABC∽△A′B′C′,的相似比为2:1,
则周长比为 ,对应边上中线之比 ,
面积之比为 .
2:1
4:1
2:1
温故知新
(2)已知△ABC∽△A′B′C′,且面积之比为1:9,
则相似比为 ,对应边上的高线之比为 ,周长之比为 .
1:3
1:3
1:3
(4)若两个相似三角形的面积比是3:4,
那么这两个三角形的周长比是_______.
(3)两个相似三角形的周长分别是10和40,
那么这两个三角形的面积比是______.
1:16
:2
3
(5)两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是120cm2 ,则较小三角形的周长___cm,面积为 cm2.
6:18=1:3
1:3=x:42
3x=42
x=14
14
1:9=y:120
y=
40
3
40
3
P
Q
S
R
A
B
C
D
例1 如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形长的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
E
要求PQ
△APQ∽△ABC
PQ // BC
PQ:BC=AE:AD
∴ ,
P
Q
S
R
A
B
C
D
E
解:如图,矩形PQRS为加工后的矩形零件,
长边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PS为xcm,则PQ为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为48cm和 24cm.
PQ
BC
AE
AD
=
x=24,
2x=48.
∴ ,
2x
80
60-x
60
=
∴ 6x=4(60-x),
AE=
AD-ED
=AD-PS
=(60-x)cm.
6x=240-4x
A
B
C
D
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
例1 如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形长的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
A
B
C
D
如图,一块铁皮呈锐角三角形,它的边BC=80cm,高AD=60cm,要把铁皮加工成矩形零件,使矩形的两边之比为2:1,且矩形的一边位于BC边上,另两个顶点分别在边AB、AC上.求这个矩形零件的边长.
方案(1)矩形长的一边位于边BC上.
方案(2)矩形短的一边位于边BC上.
A
B
C
D
方案(2)矩形短的一边位于边BC上.
P
Q
S
R
A
B
C
D
P
Q
S
R
方案(1)矩形长的一边位于边BC上.
∴ ,
P
Q
S
R
A
B
C
D
E
解:①如图,矩形PQRS为加工后的矩形零件,
长边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PS为xcm,则PQ为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为48cm和 24cm.
PQ
BC
AE
AD
=
x=24,
2x=48.
∴ ,
2x
80
60-x
60
=
∴ 6x=4(60-x),
AE=
AD-ED
=AD-PS
=(60-x)cm.
6x=240-4x
∴ ,
P
Q
S
R
A
B
C
D
E
解:②如图,矩形PQRS为加工后的矩形零件,
短边SR在边BC上,顶点P,Q分别在边AB,AC上,△ABC的高AD交PQ于点E.
设PQ为xcm,则PS为
为2xcm;
∵ PQ//BC,
∴△APQ∽△ABC,
解方程得,
答:这个矩形零件边长分别为 cm和 cm.
PQ
BC
AE
AD
=
x= ,
2x= .
∴ ,
x
80
60-2x
60
=
∴ 6x=8(60-2x),
AE=
AD-ED
=AD-PS
=(60-2x)cm.
3x=240-8x
240
11
480
11
240
11
480
11
A
B
C
D
2.已知,在△ABC中,BC=120mm,边BC上的高为80mm,在这个三角形内有一个内接矩形,矩形的一边在BC边上,另两个顶点分别在边AB,AC上.问当这个矩形面积最大时,它的边长各是多少?
P
Q
S
R
E
S矩形PQRS
=PQ · PS
=x · y
∴ ,
P
Q
S
R
A
B
C
D
E
解:如图,
设矩形PQRS的边PQ为xmm,PS
为ymm;
∵ PQ//BC,
∴△APQ∽△ABC,
PQ
BC
AE
AD
=
∴ ,
x
120
80-y
80
=
∴ y=80- x,
则AE=
AD-ED
=AD-PS
=(80-y)mm.
2
3
∵ S矩形PQRS
=PQ · PS
=x · y
∴ S矩形PQRS
=x · (80- x)
2
3
解:如图,
设矩形PQRS的边PQ为xmm,PS
为ymm;
∵ PQ//BC,
∴△APQ∽△ABC,
PQ
BC
AE
AD
=
∴ ,
∴ ,
x
120
80-y
80
=
∴ y=80- x,
则AE=
AD-ED
=AD-PS
=(80-y)mm.
2
3
∵ S矩形PQRS
=PQ · PS
=x · y
∴ S矩形PQRS
=x · (80- x)
2
3
= - x2 + 80x
2
3
∵- <0,
∴ S矩形PQRS有最大值,
2
3
此时,
x=
80
2 · (- )
2
3
-
=60(mm),
∴ y=40mm.
有相似三角形,又有垂直,就有 高的比等于 相似比.充分挖掘题目中隐含的条件、利用相似三角形对应线段的比等于相似比列方程是解题的关键.
解题心得
1.已知相似三角形面积的比为9∶4,那么这两个三角形的周长之比为( ).
A.9∶4 B.4∶9
C.3∶2 D.81∶16
C
巩固提高
2.己知两个相似三角形周长的比为3:2,
其中较小的三角形面积为12,则较大的
三角形的面积是( ).
A.27 B.24 C.18 D.16
A
A
B
C
D
3.如图,一块铁皮呈锐角三角形,它的边BC=120cm,高AD=80cm,要把铁皮加工成正方形零件,使正方形的一边GH位于BC边上,另两个顶点E、F分别在边AB、AC上.则这个正方形零件的边长为 cm.
E
F
G
H
48
今天作业
课本P90页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
