22.4 图形的位似变换(1)课件(共26张PPT)
文档属性
| 名称 | 22.4 图形的位似变换(1)课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
沪科版 九年级上册
22.4 图形的位似变换 (1)
教学目标:理解位似图形的概念和性质.会根据给
定的位似比画出位似图形.
教学重点:
用位似图形的性质画位似图形.
教学难点:
用位似图形的性质画图.
我们已经学习了图形的哪些变换?
(1)轴对称
对称轴
(2)平移:
平移的方向
平移的距离.
复习旧知
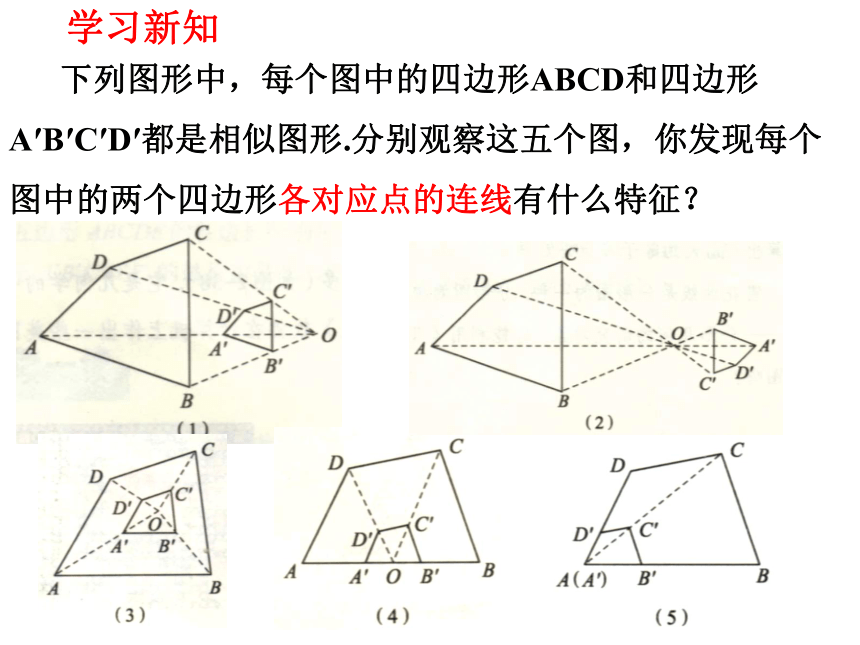
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
学习新知
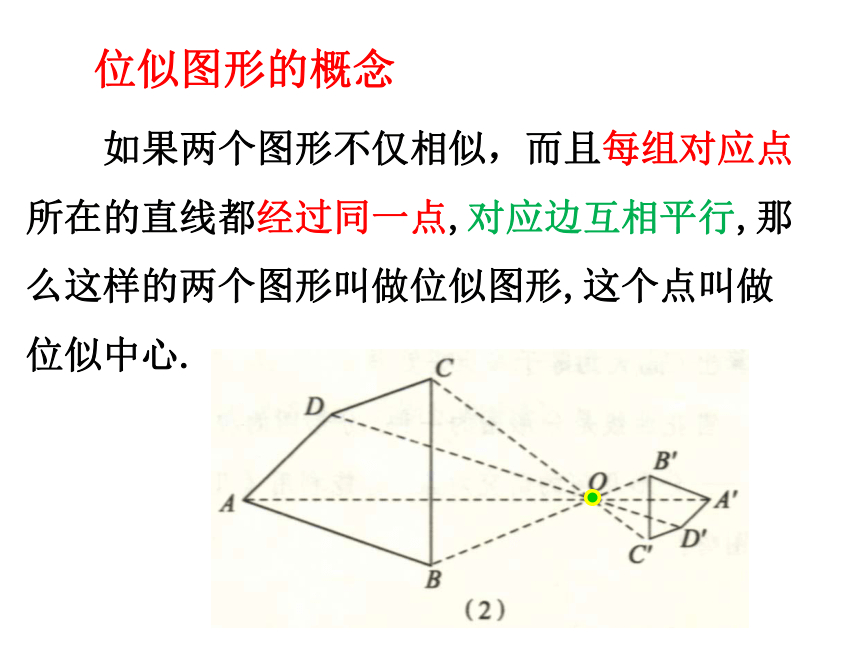
位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
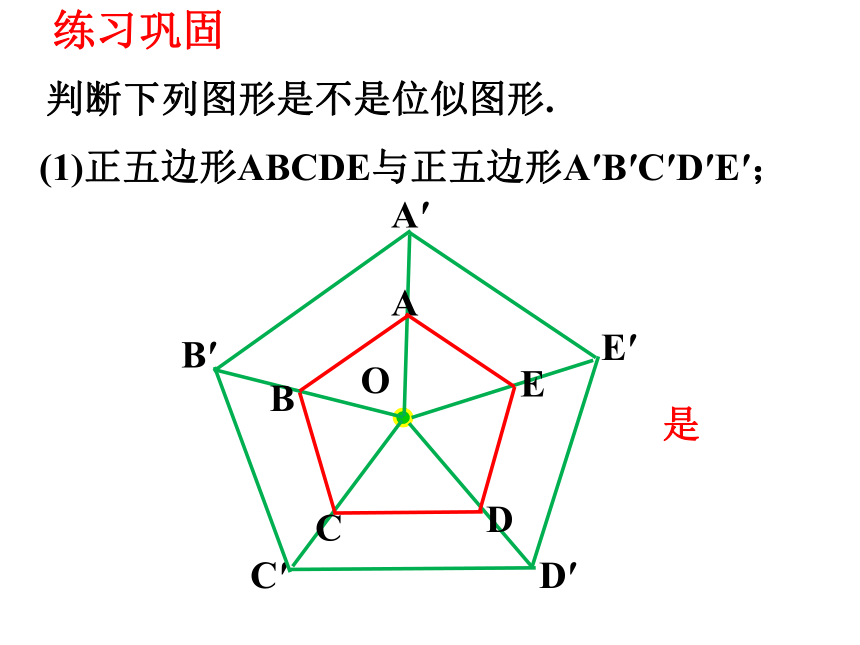
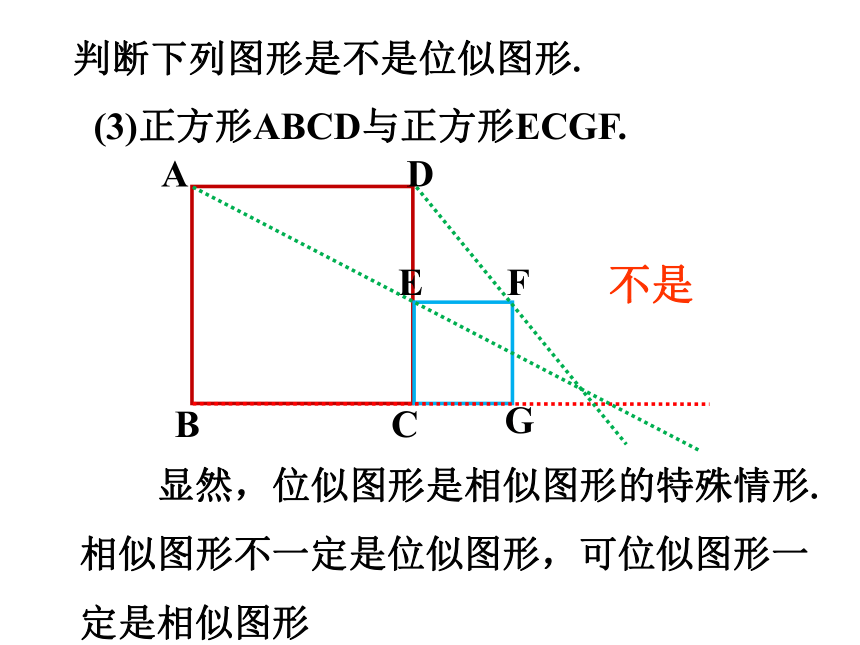
判断下列图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
是
O
A′
B′
C′
D′
E′
A
B
C
D
E
练习巩固
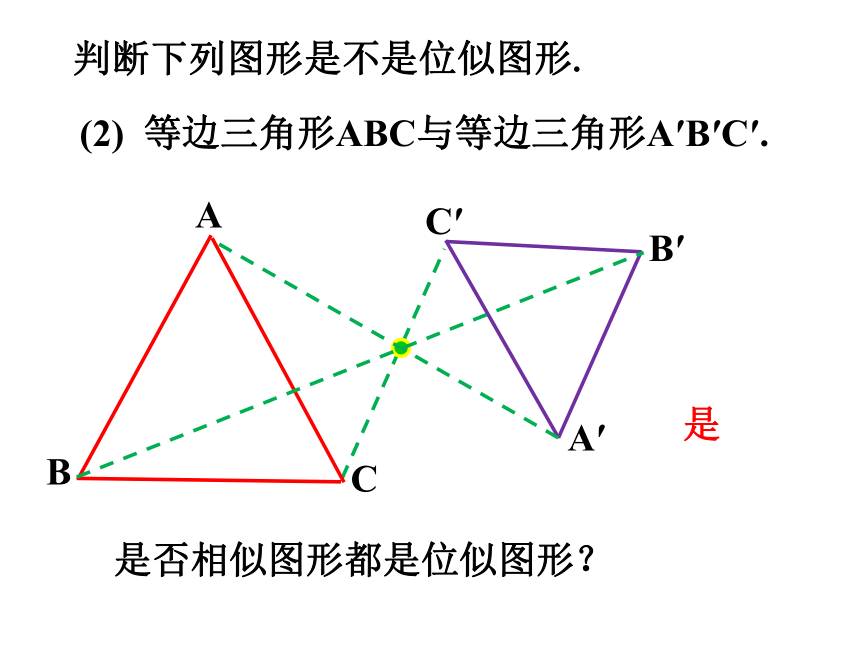
(2) 等边三角形ABC与等边三角形A′B′C′.
是否相似图形都是位似图形?
是
A
B
C
A′
B′
C′
判断下列图形是不是位似图形.
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
判断下列图形是不是位似图形.
(3)正方形ABCD与正方形ECGF.
位似是一种具有位置关系的相似.
位似图形是相似图形的特殊情形.
位似图形必定是相似图形,而相似图形不一定是位似图形.
两个位似图形的位似中心只有一个.
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
位似图形的性质
学习新知
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
O
A′
B′
C′
D′
E′
A
B
C
D
E
∵△OAB∽△OA′B′,
OA
OA′
=
=
OB
OB′
AB
A′B′
∴
2. 位似图形的性质
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
C
B
A
D
E
F
P
=
AP
AD
AF
AC
=
AE
AB
=
PF
DC
EF
BC
=
O
A′
B′
C′
D′
E′
A
B
C
D
E
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
C
B
A
D
E
F
P
(1)对应点与位似中心共线.
(2)不经过位似中心的对应边平行.
(3) 位似图形上任意一对应点到位似中心的距离之比等于位似比.
位似图形的性质
若△ABC与△A′B′C′的相似比为:1:2,则OA:OA′=( )。
1:2
O
A
B
C
C′
B′
A′
OB:OB′=?
练习巩固
O
.
A
B
C
如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
OA:OA′=1:2
A′
B′
C′
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
学习新知
思考:还有没其他作法?
O
.
A
B
A'
C
如果位似中心跑到三角形内部呢?
B'
C'
OA:OA′=1:2
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
O
A
B
C
A'
B'
C'
O
位似中心在三角形内部时
OA:OA′=1:2
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
O
A
B
C
A'
B'
C'
O
画位似图形的步骤:
1. 定中心;
2. 定关键点;
3. 定比例;
4. 连线(关键点与位似中心的连线);
5. 截新点;
6. 成形(连接新截点即画成图形).
学习新知
O
B
C
D
A
方法1:
OA′:OA=2:1
OB′:OB=2:1
OC′:OC=2:1
OD′:OD=2:1
C'
B'
A'
D'
四边形A′B′C′D'为所求.
练习1.把四边形ABCD的边长放大为原来的2倍
(即新图与原图的相似比为2).
O
B
C
D
A
练习1.把四边形ABCD的边长放大为原来的2倍
(即新图与原图的相似比为2).
方法2:
OA′:OA=2:1
OB′:OB=2:1
OC′:OC=2:1
OD′:OD=2:1
C'
B'
A'
D'
四边形A′B′C′D'为所求.
A
B
C
O
练习2 以O为中心把△ABC的边长缩小为原来
的一半.
A'
B'
C'
OA′:OA=1:2
OB′:OB=1:2
OC′:OC=1:2
△A′B′C′为所求.
方法1:
A
B
C
O
A'
B'
C'
OA′:OA=1:2
OB′:OB=1:2
OC′:OC=1:2
△A′B′C′为所求.
A′
B′
C′
方法2:
练习2 以O为中心把△ABC的边长缩小为原来
的一半.
我们学习了几种图形变换?图形经过哪种变换得到的图形与原图形全等?哪些不一定全等?
[答案] 平移、轴对称、位似变换,前两种都是全等变换,只有位似变换不一定全等.
今天作业
课本P99页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级上册
22.4 图形的位似变换 (1)
教学目标:理解位似图形的概念和性质.会根据给
定的位似比画出位似图形.
教学重点:
用位似图形的性质画位似图形.
教学难点:
用位似图形的性质画图.
我们已经学习了图形的哪些变换?
(1)轴对称
对称轴
(2)平移:
平移的方向
平移的距离.
复习旧知
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?
学习新知
位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
判断下列图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
是
O
A′
B′
C′
D′
E′
A
B
C
D
E
练习巩固
(2) 等边三角形ABC与等边三角形A′B′C′.
是否相似图形都是位似图形?
是
A
B
C
A′
B′
C′
判断下列图形是不是位似图形.
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
判断下列图形是不是位似图形.
(3)正方形ABCD与正方形ECGF.
位似是一种具有位置关系的相似.
位似图形是相似图形的特殊情形.
位似图形必定是相似图形,而相似图形不一定是位似图形.
两个位似图形的位似中心只有一个.
两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
位似图形的性质
学习新知
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
O
A′
B′
C′
D′
E′
A
B
C
D
E
∵△OAB∽△OA′B′,
OA
OA′
=
=
OB
OB′
AB
A′B′
∴
2. 位似图形的性质
位似图形上任意一对对应点到位似中心的距离之比等于相似比.
C
B
A
D
E
F
P
=
AP
AD
AF
AC
=
AE
AB
=
PF
DC
EF
BC
=
O
A′
B′
C′
D′
E′
A
B
C
D
E
2. 位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比.
C
B
A
D
E
F
P
(1)对应点与位似中心共线.
(2)不经过位似中心的对应边平行.
(3) 位似图形上任意一对应点到位似中心的距离之比等于位似比.
位似图形的性质
若△ABC与△A′B′C′的相似比为:1:2,则OA:OA′=( )。
1:2
O
A
B
C
C′
B′
A′
OB:OB′=?
练习巩固
O
.
A
B
C
如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
OA:OA′=1:2
A′
B′
C′
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
学习新知
思考:还有没其他作法?
O
.
A
B
A'
C
如果位似中心跑到三角形内部呢?
B'
C'
OA:OA′=1:2
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
O
A
B
C
A'
B'
C'
O
位似中心在三角形内部时
OA:OA′=1:2
OB:OB′=1:2
OC:OC′=1:2
△A′B′C′为所求.
O
A
B
C
A'
B'
C'
O
画位似图形的步骤:
1. 定中心;
2. 定关键点;
3. 定比例;
4. 连线(关键点与位似中心的连线);
5. 截新点;
6. 成形(连接新截点即画成图形).
学习新知
O
B
C
D
A
方法1:
OA′:OA=2:1
OB′:OB=2:1
OC′:OC=2:1
OD′:OD=2:1
C'
B'
A'
D'
四边形A′B′C′D'为所求.
练习1.把四边形ABCD的边长放大为原来的2倍
(即新图与原图的相似比为2).
O
B
C
D
A
练习1.把四边形ABCD的边长放大为原来的2倍
(即新图与原图的相似比为2).
方法2:
OA′:OA=2:1
OB′:OB=2:1
OC′:OC=2:1
OD′:OD=2:1
C'
B'
A'
D'
四边形A′B′C′D'为所求.
A
B
C
O
练习2 以O为中心把△ABC的边长缩小为原来
的一半.
A'
B'
C'
OA′:OA=1:2
OB′:OB=1:2
OC′:OC=1:2
△A′B′C′为所求.
方法1:
A
B
C
O
A'
B'
C'
OA′:OA=1:2
OB′:OB=1:2
OC′:OC=1:2
△A′B′C′为所求.
A′
B′
C′
方法2:
练习2 以O为中心把△ABC的边长缩小为原来
的一半.
我们学习了几种图形变换?图形经过哪种变换得到的图形与原图形全等?哪些不一定全等?
[答案] 平移、轴对称、位似变换,前两种都是全等变换,只有位似变换不一定全等.
今天作业
课本P99页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
