3.1.1一元一次方程 课件(共29张PPT)
文档属性
| 名称 | 3.1.1一元一次方程 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 11:50:00 | ||
图片预览







文档简介
(共29张PPT)
3.1.1一元一次方程
人教版 七年级上册
教学目标
教学目标:
1.通过处理实际问题,让学生体验从算术方法到代数方法是一种进步;
2.初步学会如何寻找问题中的相等关系,列出方程,了解方程的概念;
3.培养学生获取信息,分析问题,处理问题的能力。
重点:从实际问题中寻找相等关系
难点:从实际问题中寻找相等关系
复习回顾
在小学,我们已经见过像 2x=50,3x+1=4,5x-7=8 这样简单的方程,还有下面列出的式子:
又如:
|x+5| =2
x2 –8x+2=0
x+1=2x-5
6x-11=12
如:
含有未知数的等式叫做方程.
复习回顾
你能判断出下列各式哪些是方程吗?
(1) ( ) (2) ( )
(3) ( ) (4) ( )
(5) ( ) (6) ( )
√
×
√
×
√
×
新知探究
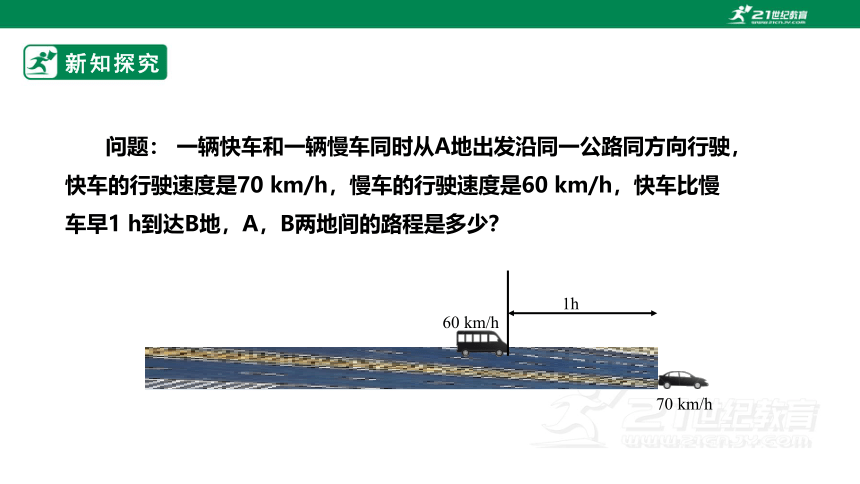
问题: 一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h到达B地,A,B两地间的路程是多少?
1h
60 km/h
70 km/h
新知探究
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
新知探究
(2)如果将AB之间的路程用x表示,用含x的式子表示下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
A
B
快车
慢车
1h
方程
新知探究
(3)如果用y表示快车行完AB的总时间,你能从快车与慢车的路程关系中找到等量关系,从而列出方程吗?
方 程: 70 y =60(y+1)
等量关系: 快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
新知探究
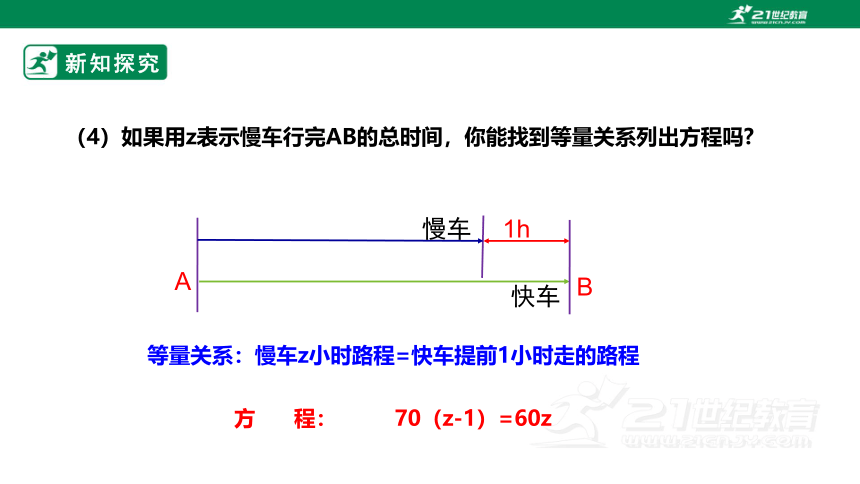
(4)如果用z表示慢车行完AB的总时间,你能找到等量关系列出方程吗
方 程: 70(z-1)=60z
等量关系:慢车z小时路程=快车提前1小时走的路程
A
B
快车
慢车
1h
新知探究
比较用算术方法和列方程解题的特点?
用算术方法解 用方程解
未知数不参加列式 未知数用字母表示来列式
根据题中的已知数和未知数间的关系,确定解答步骤,再列式计算 根据题意找出数量间的相等关系列出含有未知数的等式
提示:通常用x、y、z等字母表示未知数。
新知讲解
列方程时,要先设字母表示未知数,然后根据问题中的相等关系,写出含有未知数的等式——方程.
通常用x,y,z等字母表示未知数,法国数学家笛卡儿是最早这样做的人.我国古代用“天元、地元、人元、物元”等表示未知数.
例题解析
例1 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形
的边长是多少?
解:设正方形的边长为x cm.
列方程
4x = 24.
边长×4 =周长.
分析:
例题解析
(2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定的检修时间2450 h?
解: 设x月后这台计算机的使用时间达到2450 h,那么在x月里这台计算机使用了150x h.
列方程
1700 + 150x = 2450
分析:
已使用时间+再使用时间=规定检修时间
例题解析
(3)某校女生占全体学生人数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x,那么女生数为
0.52x,男生数为(1-0.52)x.
列方程
0.52x-(1 - 0.52)x= 80
分析:
女生人数=0.52×全体学生人数
新知讲解
4x=24;
1700+150x=2450; 0.52x=(1-0.52)x+80.
(1)只含有一个未知数
(2)未知数的次数都是1
(3)等号两边都是整式
观察上面的方程,它们有什么共同特点?
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
对点训练
判断下列方程是否是一元一次方程 并说明理由.
不是
不是
是
数或字母的积
几个单项式的和
不是
新知讲解
列一元一次方程的步骤:
1.设:恰当的设出未知数,用字母x表示问题中的未知量。
2.找:寻找实际问题中的相等关系(关键)。
3.列:利用实际问题中的相等关系列出方程。
实际问题
一元一次方程
设未知数
列方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法。
新知讲解
当x=6时,方程等号左右两边相等,所以x=6是该方程的解,也就是说未知数x的值为6
当x=5时,方程等号左右两边相等,所以x=5是该方程的解,也就是说未知数x的值为5
使方程等号左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
新知讲解
探究:x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80 的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当 x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
归纳总结
1. 将数值代入方程左边进行计算;
2. 将数值代入方程右边进行计算;
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
课堂练习
1.下列各式,哪些是一元一次方程?
(2)3x+1=7
(1)3x+1
(3)3x+y=7
(4)3x2+1=7x
√
×
错因:不是等式.
×
错因:有两个未知数.
×
错因:未知数的次数是2.
×
错因:分母中含有未知数,
不是整式.
课堂练习
2.下列各式是一元一次方程的是( )
A.x2-2x=1 B.x-1=
C.y+3=x-4 D.
3.下列说法正确的是( )
A.方程x-3=1的解是x=-2 B.方程 x-2x=6的解是x=-4
C.方程- x=2的解是x=- D.方程3x-4= (x-3)的解是x=3
D
B
课堂练习
5. 若 x =1是方程x2 -2mx +1=0的一个解,则m的值为( )
A. 0 B. 2 C. 1 D. -1
4. x =1是下列哪个方程的解( )
A. B.
C. D.
B
C
课堂练习
6. 根据条件列出等式:
(1)比a大5的数等于8
___________________
a+5=8
(2)b的三分之一等于9
___________________
b=9
(3)x的2倍与10的和等于18
___________________
2x+10=18
课堂练习
7. 列方程:
(1)某校七年级(1)班共有学生48人,其中女生人数比男生人数的 多3人,这个班有男生多少人?
解:设这个班有男生x人
x+( x+3)=48
(2)把1400元奖学金按照两种奖项奖给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生有多少人?
解:设获得一等奖的学生有x人
200x+50(22-x)=1400
课堂练习
8.若方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程.
(1)求m的值;
(2)判断x=3,x=- ,x= 是否是方程的解.
解:(1)由题意可得|m|-2=0,且m+2≠0,
∴m=2;
(2)由(1)知原方程为-4x-6=0,
故x=- 是方程的解,x=3,x= 不是方程的解.
课堂总结
1.方程:含有未知数的等式.
3.列方程解决实际问题的关键:
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,
且等号两边都是整式,这样的方程叫做一元一次方程.
(1)审(抓关键词句,找相等关系.)
(2)设(设未知数,用代数式表示未知量.)
(3)列(根据相等关系列方程.)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1.1一元一次方程
人教版 七年级上册
教学目标
教学目标:
1.通过处理实际问题,让学生体验从算术方法到代数方法是一种进步;
2.初步学会如何寻找问题中的相等关系,列出方程,了解方程的概念;
3.培养学生获取信息,分析问题,处理问题的能力。
重点:从实际问题中寻找相等关系
难点:从实际问题中寻找相等关系
复习回顾
在小学,我们已经见过像 2x=50,3x+1=4,5x-7=8 这样简单的方程,还有下面列出的式子:
又如:
|x+5| =2
x2 –8x+2=0
x+1=2x-5
6x-11=12
如:
含有未知数的等式叫做方程.
复习回顾
你能判断出下列各式哪些是方程吗?
(1) ( ) (2) ( )
(3) ( ) (4) ( )
(5) ( ) (6) ( )
√
×
√
×
√
×
新知探究
问题: 一辆快车和一辆慢车同时从A地出发沿同一公路同方向行驶,快车的行驶速度是70 km/h,慢车的行驶速度是60 km/h,快车比慢车早1 h到达B地,A,B两地间的路程是多少?
1h
60 km/h
70 km/h
新知探究
(1) 上述问题中涉及到了哪些量?
快车70 km/h,慢车60 km/h
快车比慢车早1h经过B地
AB之间的路程
速度:
时间:
路程:
A
B
快车
慢车
1h
快车每小时比慢车多走10km
60km
相同的时间,快车比慢车多走60km
快车走了6h
算式:60 ÷(70-60)×70=420(km)
新知探究
(2)如果将AB之间的路程用x表示,用含x的式子表示下列时间关系:
快车行完AB全程所用时间:
慢车行完AB全程所用时间:
两车所用的时间关系为:快车比慢车早到1h
即:( )- ( )=1
慢车用时
快车用时
A
B
快车
慢车
1h
方程
新知探究
(3)如果用y表示快车行完AB的总时间,你能从快车与慢车的路程关系中找到等量关系,从而列出方程吗?
方 程: 70 y =60(y+1)
等量关系: 快车y小时路程=慢车(y+1)小时路程
A
B
快车
慢车
1h
新知探究
(4)如果用z表示慢车行完AB的总时间,你能找到等量关系列出方程吗
方 程: 70(z-1)=60z
等量关系:慢车z小时路程=快车提前1小时走的路程
A
B
快车
慢车
1h
新知探究
比较用算术方法和列方程解题的特点?
用算术方法解 用方程解
未知数不参加列式 未知数用字母表示来列式
根据题中的已知数和未知数间的关系,确定解答步骤,再列式计算 根据题意找出数量间的相等关系列出含有未知数的等式
提示:通常用x、y、z等字母表示未知数。
新知讲解
列方程时,要先设字母表示未知数,然后根据问题中的相等关系,写出含有未知数的等式——方程.
通常用x,y,z等字母表示未知数,法国数学家笛卡儿是最早这样做的人.我国古代用“天元、地元、人元、物元”等表示未知数.
例题解析
例1 根据下列问题,设未知数并列出方程:
(1)用一根长24 cm的铁丝围成一个正方形,正方形
的边长是多少?
解:设正方形的边长为x cm.
列方程
4x = 24.
边长×4 =周长.
分析:
例题解析
(2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定的检修时间2450 h?
解: 设x月后这台计算机的使用时间达到2450 h,那么在x月里这台计算机使用了150x h.
列方程
1700 + 150x = 2450
分析:
已使用时间+再使用时间=规定检修时间
例题解析
(3)某校女生占全体学生人数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x,那么女生数为
0.52x,男生数为(1-0.52)x.
列方程
0.52x-(1 - 0.52)x= 80
分析:
女生人数=0.52×全体学生人数
新知讲解
4x=24;
1700+150x=2450; 0.52x=(1-0.52)x+80.
(1)只含有一个未知数
(2)未知数的次数都是1
(3)等号两边都是整式
观察上面的方程,它们有什么共同特点?
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
对点训练
判断下列方程是否是一元一次方程 并说明理由.
不是
不是
是
数或字母的积
几个单项式的和
不是
新知讲解
列一元一次方程的步骤:
1.设:恰当的设出未知数,用字母x表示问题中的未知量。
2.找:寻找实际问题中的相等关系(关键)。
3.列:利用实际问题中的相等关系列出方程。
实际问题
一元一次方程
设未知数
列方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法。
新知讲解
当x=6时,方程等号左右两边相等,所以x=6是该方程的解,也就是说未知数x的值为6
当x=5时,方程等号左右两边相等,所以x=5是该方程的解,也就是说未知数x的值为5
使方程等号左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
新知讲解
探究:x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80 的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当 x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
归纳总结
1. 将数值代入方程左边进行计算;
2. 将数值代入方程右边进行计算;
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
课堂练习
1.下列各式,哪些是一元一次方程?
(2)3x+1=7
(1)3x+1
(3)3x+y=7
(4)3x2+1=7x
√
×
错因:不是等式.
×
错因:有两个未知数.
×
错因:未知数的次数是2.
×
错因:分母中含有未知数,
不是整式.
课堂练习
2.下列各式是一元一次方程的是( )
A.x2-2x=1 B.x-1=
C.y+3=x-4 D.
3.下列说法正确的是( )
A.方程x-3=1的解是x=-2 B.方程 x-2x=6的解是x=-4
C.方程- x=2的解是x=- D.方程3x-4= (x-3)的解是x=3
D
B
课堂练习
5. 若 x =1是方程x2 -2mx +1=0的一个解,则m的值为( )
A. 0 B. 2 C. 1 D. -1
4. x =1是下列哪个方程的解( )
A. B.
C. D.
B
C
课堂练习
6. 根据条件列出等式:
(1)比a大5的数等于8
___________________
a+5=8
(2)b的三分之一等于9
___________________
b=9
(3)x的2倍与10的和等于18
___________________
2x+10=18
课堂练习
7. 列方程:
(1)某校七年级(1)班共有学生48人,其中女生人数比男生人数的 多3人,这个班有男生多少人?
解:设这个班有男生x人
x+( x+3)=48
(2)把1400元奖学金按照两种奖项奖给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生有多少人?
解:设获得一等奖的学生有x人
200x+50(22-x)=1400
课堂练习
8.若方程(|m|-2)x2-(m+2)x-6=0是关于x的一元一次方程.
(1)求m的值;
(2)判断x=3,x=- ,x= 是否是方程的解.
解:(1)由题意可得|m|-2=0,且m+2≠0,
∴m=2;
(2)由(1)知原方程为-4x-6=0,
故x=- 是方程的解,x=3,x= 不是方程的解.
课堂总结
1.方程:含有未知数的等式.
3.列方程解决实际问题的关键:
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,
且等号两边都是整式,这样的方程叫做一元一次方程.
(1)审(抓关键词句,找相等关系.)
(2)设(设未知数,用代数式表示未知量.)
(3)列(根据相等关系列方程.)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
