第一单元长方体和正方体解答题过关练习(专项突破)-小学数学六年级上册苏教版(含解析)
文档属性
| 名称 | 第一单元长方体和正方体解答题过关练习(专项突破)-小学数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 11:58:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一单元长方体和正方体解答题过关练习(专项突破)-小学数学六年级上册苏教版
一、解答题
1.(1)小明家新买了一台洗衣机,请你帮他算一算,放置这台洗衣机要占多大面积?
(2)如果给洗衣机缝制一个布罩,至少需要多大面积的布料?(接缝处忽略不计,底面不需要)
2.惠民超市要做一个长5米、宽0.5米、高0.8米的玻璃柜台,至少需要多大面积的玻璃?
3.笑笑的房间长3.5米,宽3米,高3米,除去门窗4.5平方米,房间的墙壁和房顶都刷上涂料。每平方米用涂料0.28千克,至少需要涂料多少千克?
4.端午节这天,妈妈买了4盒绿豆糕,准备把这4盒绿豆糕包在一起,一盒绿豆糕的长、宽、高分别是15厘米、10厘米和4厘米,怎样包装最节省包装纸?至少需要包装纸多少平方厘米?(接口处不计)
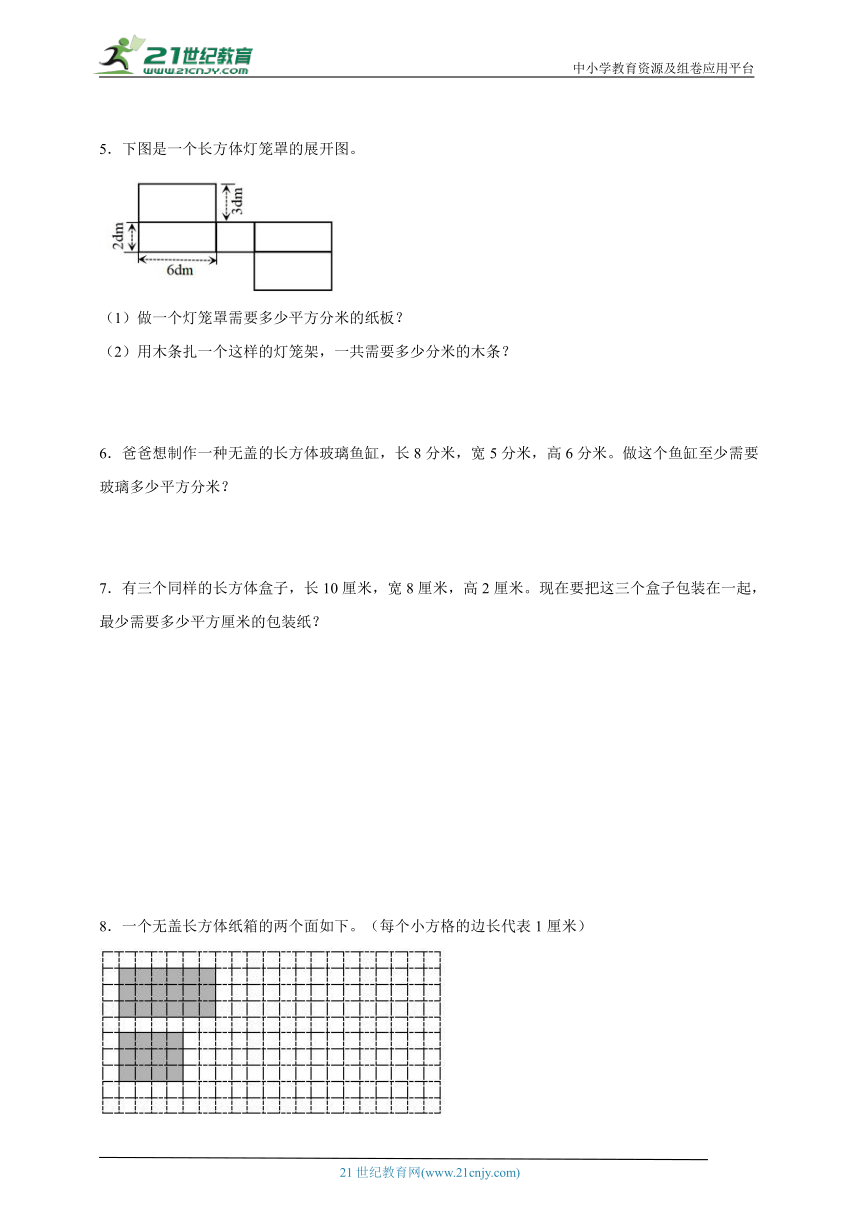
5.下图是一个长方体灯笼罩的展开图。
(1)做一个灯笼罩需要多少平方分米的纸板?
(2)用木条扎一个这样的灯笼架,一共需要多少分米的木条?
6.爸爸想制作一种无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。做这个鱼缸至少需要玻璃多少平方分米?
7.有三个同样的长方体盒子,长10厘米,宽8厘米,高2厘米。现在要把这三个盒子包装在一起,最少需要多少平方厘米的包装纸?
8.一个无盖长方体纸箱的两个面如下。(每个小方格的边长代表1厘米)
(1)请你画出长方体纸箱其他的三个面。
(2)计算长方体纸箱的表面积。
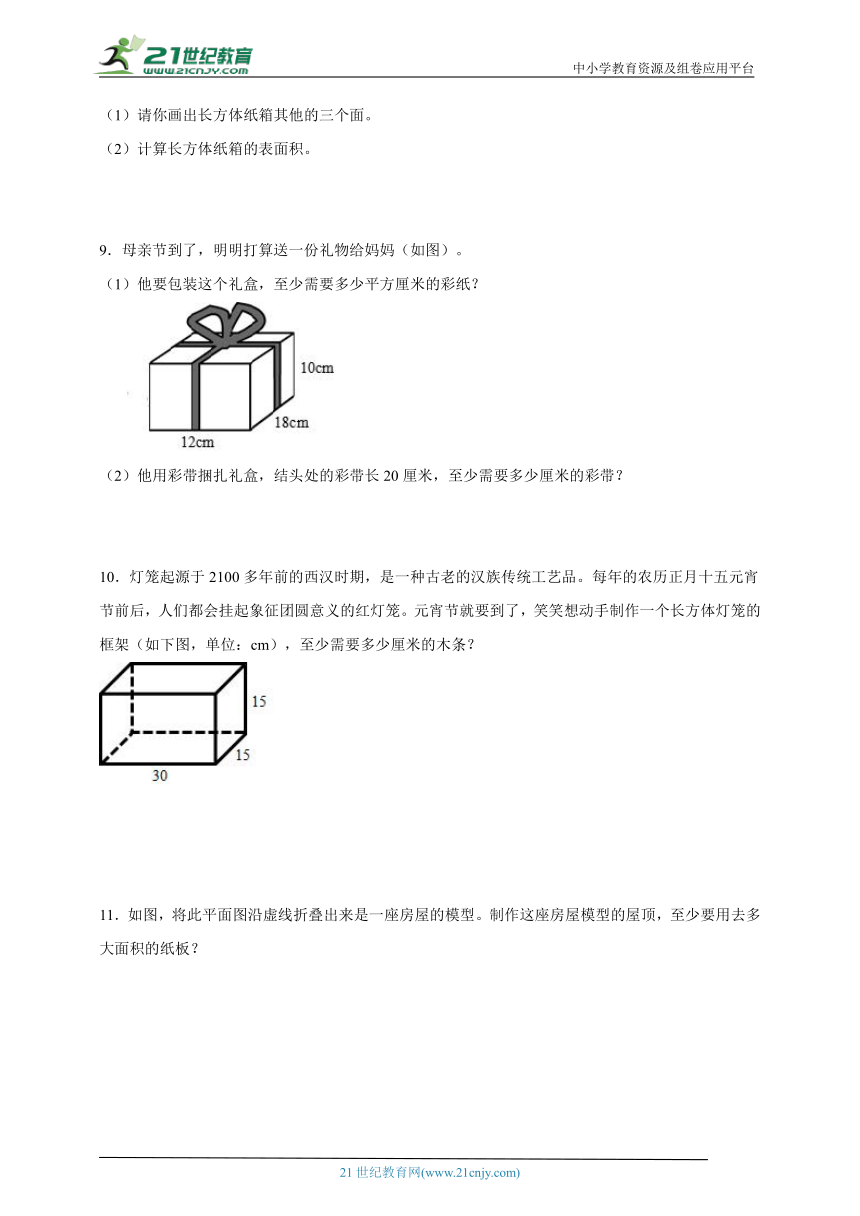
9.母亲节到了,明明打算送一份礼物给妈妈(如图)。
(1)他要包装这个礼盒,至少需要多少平方厘米的彩纸?
(2)他用彩带捆扎礼盒,结头处的彩带长20厘米,至少需要多少厘米的彩带?
10.灯笼起源于2100多年前的西汉时期,是一种古老的汉族传统工艺品。每年的农历正月十五元宵节前后,人们都会挂起象征团圆意义的红灯笼。元宵节就要到了,笑笑想动手制作一个长方体灯笼的框架(如下图,单位:cm),至少需要多少厘米的木条?
11.如图,将此平面图沿虚线折叠出来是一座房屋的模型。制作这座房屋模型的屋顶,至少要用去多大面积的纸板?
12.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是多少?
从上面看 从正面看
13.淘气家有一个长方体玻璃鱼缸,从里面量长8分米,宽4分米,高6分米,里面水深2.5分米。
(1)容器与水接触部分的面积是多少平方分米?
(2)如果全部装满水,能装多少升?
(3)在鱼缸中放入一个假山石(全部浸没在水中),结果水面上升1厘米,假山石的体积是多少立方分米?
14.某快递运货车的车厢是长方体,从里面量长5米、宽2.5米、高2米。它的容积是多少立方米?
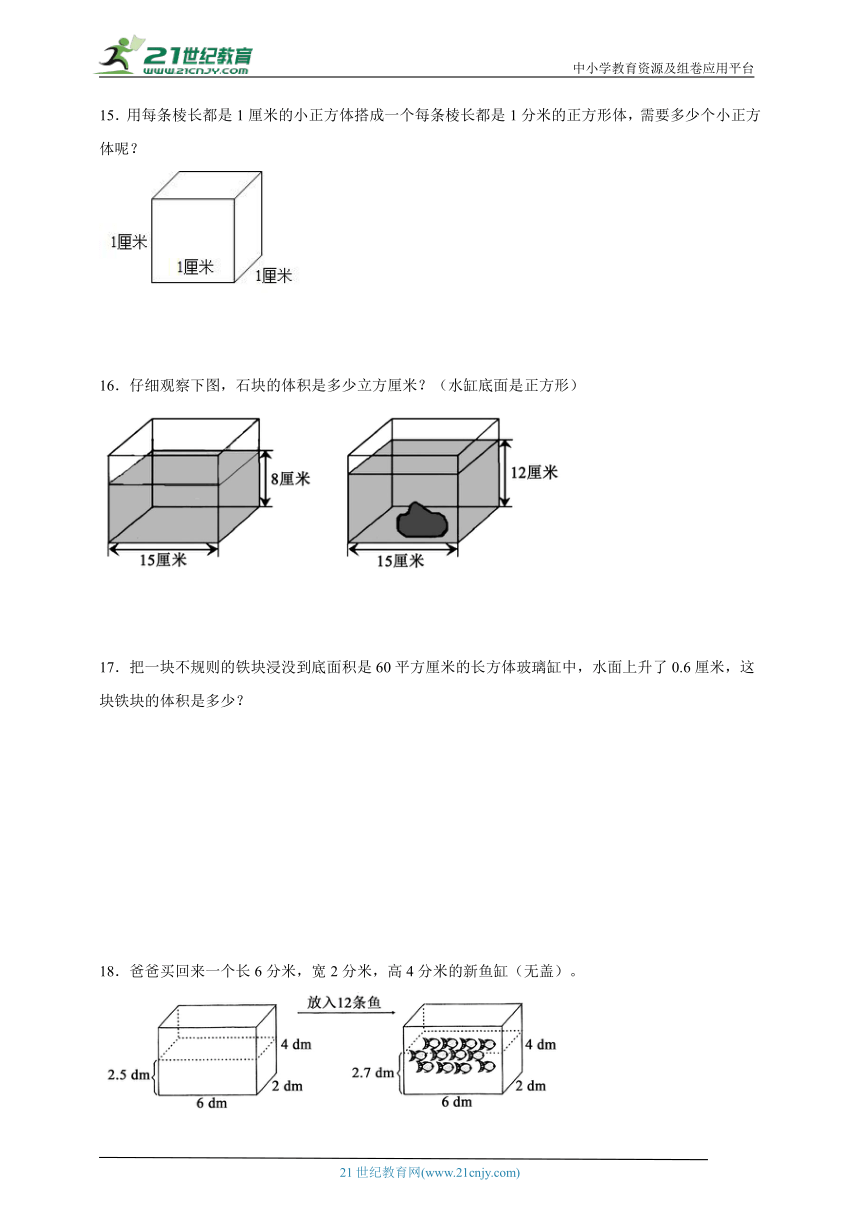
15.用每条棱长都是1厘米的小正方体搭成一个每条棱长都是1分米的正方形体,需要多少个小正方体呢?
16.仔细观察下图,石块的体积是多少立方厘米?(水缸底面是正方形)
17.把一块不规则的铁块浸没到底面积是60平方厘米的长方体玻璃缸中,水面上升了0.6厘米,这块铁块的体积是多少?
18.爸爸买回来一个长6分米,宽2分米,高4分米的新鱼缸(无盖)。
(1)做这个鱼缸至少用了多少平方分米的玻璃?
(2)鱼缸里的每条鱼平均体积是多少?
19.把一块长32cm的长方形铁皮,在四角上剪去边长为4cm的小正方形,再做成无盖的盒子,盒子的容积是768mL。做这个盒子用了多少平方厘米的铁皮?
20.一个长方体玻璃容器长30厘米,宽25厘米,高16厘米。
(1)这个容器的容积是多少升?
(2)把一块石头放入这个盛有水的长方体容器中,石头被水完全浸没,水面高13厘米,把石头取出后,水面降低了2厘米,这块石头的体积是多少立方厘米?
21.一个长5分米、宽4分米、深3分米的长方体水缸里放入一个小石块,然后注满水(水完全浸没小石块),当取出小石块后,水面下降到1.8分米。小石块的体积是多少立方分米?
参考答案:
1.(1)3000平方厘米
(2)21700平方厘米
【分析】(1)观察图形可知,这台洗衣机是一个长方体,求它的占地面积,就是求长方体的底面积,根据长方形面积公式:面积=长×宽,代入数据,求出占地面积;
(2)求需要多大面积的布料,就是求这个长方体洗衣机去掉一个底面的5个面的面积和,根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】(1)60×50=3000(平方厘米)
答:放置这台洗衣机要占3000平方厘米大的面积。
(2)60×50+(60×85+50×85)×2
=3000+(5100+4250)×2
=3000+9350×2
=3000+18700
=21700(平方厘米)
答:至少需要21700平方厘米的布料。
【点睛】利用长方形面积公式和长方体表面积公式进行解答,关键熟记公式。
2.13.8平方米
【分析】求至少需要多大面积的玻璃,即求长方体的表面积,根据长方体表面积公式S=(ab+ah+bh)×2,代入数值计算即可。
【详解】(5×0.5+5×0.8+0.5×0.8)×2
=(2.5+4+0.4)×2
=6.9×2
=13.8(平方米)
答:至少需要13.8平方米面积的玻璃。
【点睛】本题考查长方体表面积公式的应用,关键是牢记公式。
3.12.6千克
【分析】根据题意,先根据长方体表面积公式,求出笑笑房间5个面的面积和,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出笑笑房间的表面积;再减去门窗的面积,就是要刷上涂料的面积,再乘0.28,就是至少需要涂料多少千克。
【详解】3.5×3+(3.5×3+3×3)×2-4.5
=10.5+(10.5+9)×2-4.5
=10.5+19.5×2-4.5
=10.5+39-4.5
=49.5-4.5
=45(平方米)
45×0.28=12.6(千克)
答:至少需要涂料12.6千克。
【点睛】利用长方体表面积公式进行解答,关键是熟记公式。
4.1100平方厘米
【分析】把这两个长方体盒子的15×10面相粘合,得到的大长方体的表面积最小,比原来两个盒子的表面积减少了2个最大的面,最节约包装纸,由此解答即可。
【详解】将15×10这个面重合摞在一起,拼成一个长15cm,宽10cm,高16cm的长方体最节约包装纸。
(15×10+15×16+16×10)×2
=(150+240+160)×2
=550×2
=1100(平方厘米)
答:至少需要包装纸1100平方厘米。
【点睛】抓住两个长方体拼组一个大长方体的方法:最大面相粘合,得到的大长方体的表面积最小;最小面相粘合,得到的大长方体的表面积最大。
5.(1)72平方分米
(2)44分米
【分析】(1)根据图形可知,长方体的长是6分米,宽是2分米,高是3分米,求做一个灯笼需要多少平方分米的纸板,就是求这个长方体的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)求需要多少分米的木条,就是求这个长方体的棱长总和,根据长方体棱长总和公式:(长+宽+高)×4,代入数据,即可解答。
【详解】(6×2+6×3+2×3)×2
=(12+18+6)×2
=(30+6)×2
=36×2
=72(平方分米)
答:做一个灯笼需要72平方分米纸板。
(2)(6+2+3)×4
=(8+3)×4
=11×4
=44(分米)
答:一共需要44分米的木条。
【点睛】利用长方体表面积公式、棱长总和公式进行解答;关键是确定长方体的长、宽和高的长度。
6.196平方分米
【分析】根据无盖长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解。
【详解】8×5+(8×6+5×6)×2
=40+(48+30)×2
=40+78×2
=40+156
=196(平方分米)
答:做这个鱼缸至少需要玻璃196平方分米。
【点睛】本题主要考查无盖长方体的表面积公式,熟练掌握它的公式并灵活运用。
7.376平方厘米
【分析】把三个长方体盒子叠在一起,有3种方式,重叠面积最大的叠法最省包装纸,即重叠底面时最省包装纸,据此解答。
【详解】因为三个面中底面最大,所以重合放在一起最省包装纸。
长方体的长是10厘米,宽是8厘米,高是2×3=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=(140+48)×2
=188×2
=376(平方厘米)
答:最少需要376平方厘米的包装纸。
【点睛】最大面重合,得到的长方体的表面积最小,最小面重合,得到的长方体表面积最大。
8.(1)见详解
(2)90平方厘米
【分析】(1)根据图形可知,长是6厘米,宽是3厘米的长方形是这个长方体的底面;再根据下面图形可知,长方体的高是4厘米;由此画出一个长是4厘米,宽是3厘米的长方形;再画出两个长是6厘米,宽是4厘米的长方形,就是这个长方体纸箱的其他的三个面;
(2)根据长方体的特征,长方体的长是6厘米,宽是3厘米,高是4厘米,根据无盖长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】(1)
(2)长方体的长是6厘米,宽是3厘米,高是4厘米。
表面积:6×3+(6×4+3×4)×2
=18+(24+12)×2
=18+36×2
=18+72
=90(平方厘米)
答:长方体的纸盒箱的表面积是90平方厘米。
【点睛】利用长方体的特征以及长方体表面积公式进行解答。
9.(1)1032平方厘米
(2)120厘米
【分析】(1)求包装这个礼盒需要多少平方厘米的彩纸,就是求这个礼盒的表面积,根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体的特征,它的12条棱分为互相平行(相对)的3组,每组4条棱的长度相等,由题意可知,彩带的长度就是长×2+宽×2+高×4+结头处彩带的长度,代入数据,即可解答。
【详解】(1)(12×18+12×10+18×10)×2
=(216+120+180)×2
=(336+180)×2
=516×2
=1032(平方厘米)
答:至少需要1032平方厘米的彩纸。
(2)12×2+18×2+10×4+20
=24+36+40+20
=60+40+20
=120(厘米)
答:至少需要120厘米的彩带。
【点睛】利用长方体的表面积公式,长方体的特征以及棱长总和公式的应用进行解答。
10.240厘米
【分析】根据题意,求制作这个长方体灯笼的框架,需要多少厘米的木条,就是求这个长方体的棱长总和,根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,代入数据,即可解答。
【详解】(30+15+15)×4
=(45+15)×4
=60×4
=240(厘米)
答:至少需要240厘米的木条。
【点睛】利用长方体棱长总和的公式进行解答,关键是熟记公式。
11.32平方厘米
【分析】先将平面图折叠成立体图,判断出房屋模型中的屋顶面是哪个面,然后根据屋顶面形状,求出它的大小。在此模型中,屋顶面是由两个长方形面组成,所以运用长方形面积计算公式计算即可。
【详解】由分析可知:屋顶是由两个长为8厘米,宽为2厘米的长方形组成的。
8×2×2
=16×2
=32(平方厘米)
答:至少要用去32平方厘米的纸板。
【点睛】本题主要考查对图形的展开与折叠灵活运用。
12.7cm3
【分析】这个图形从正面看到5个小正方体,这5个小正方体可以分成3列,左右两列有2个正方体,中间一列有1个正方体。从上面看到两行,下面一行3个正方体,上面一行1个正方体,左对齐。下面一行的3个正方体是从正面看到的5个正方体中的3个。因为从正面看左面一列有2个正方体,所以上面一行的1个正方体表示这一列最多有2个正方体,则这个几何体最多有5+2=7个正方体,据此解答。
【详解】由分析得:
这个几何体最多有7个正方体,棱长为1cm的小正方体的体积是1cm3,则这个几何体的体积最大是7cm3。
【点睛】本题考查从不同方向观察物体,关键是明确这个几何体最多有几个小正方体,需要学生有较强的空间想象和推理能力。
13.(1)92平方分米;
(2)192升;
(3)3.2立方分米
【分析】(1)求容器与水接触部分的面积,实际上是求这个长方体容器4个侧面和1个底面的面积之和,可根据长方形的表面积公式:S=a×b+a×h×2+b×h×2,代入数据,即可求出长方体的表面积。
(2)求装满水的体积,实际上是求容器的容积,根据长方体的体积(容积)公式:V=abh,代入长宽高的数据,求出结果后,再进行单位换算即可。
(3)放入假山石后,假山的体积等于水面上升的的体积,这部分体积可以看作长为8分米、宽为4分米,高为1厘米的长方体的体积,注意计算前要换算高的单位,再利用长方体的体积公式:V=abh,代入即可求出假山石的体积。
【详解】(1)8×4+8×2.5×2+4×2.5×2
=32+40+20
=92(平方分米)
答:容器与水接触部分的面积是92平方分米。
(2)8×4×6=192(立方分米)
192立方分米=192升
答:如果全部装满水,能装192升。
(3)1厘米=0.1分米
8×4×0.1=3.2(立方分米)
答:假山石的体积是3.2立方分米。
【点睛】此题主要考查长方体表面积、体积的综合运用,熟记表面积和体积的公式,通过转化的数学思想,根据长方体的体积公式,求出不规则物体的体积。
14.25立方米
【分析】首先要清楚这道题是求长方体的容积,容积的计算方法和体积是一样的,就用长乘宽再乘高,列式计算即可解决。
【详解】5×2.5×2=25(立方米)
答:它的容积是25立方米。
【点睛】此题主要考查长方体容积的实际应用,长方体的容积计算公式:长方体的容积=长×宽×高。
15.1000个
【分析】1分米=10厘米,用小正方形撘成大正方体,可以摆10层,每层可以摆10行,10列。则每层有10×10=100个小正方体,一共有100×10=1000个小正方体。据此解答。
【详解】1分米=10厘米
10×10×10=1000(个)
答:需要1000个小正方体。
【点睛】解决本题时应先求出小正方体摆放层数,每层摆放个数,再求出小正方体个数,旨在考查学生的空间想象和推理能力。
16.900立方厘米
【分析】由题可知,水面上升的体积等于石块的体积,根据长方体的体积公式:V=abh,代入数据计算即可。
【详解】
=225×4
=900(立方厘米)
答:石块的体积是900立方厘米。
【点睛】本题的关键是理解石块的体积等于水面上升的体积,还可以用上升后的体积减去上升前的体积,也可以解答。
17.36立方厘米
【分析】根据题意可知,铁块的体积等于水面上升部分的体积;根据长方体体积公式:底面积×高,代入数据,即可解答。
【详解】60×0.6=36(立方厘米)
答:这块铁块的体积是立方厘米。
【点睛】本题考查不规则物体体积的求法,关键明确铁块的体积与水面上升部分之间的关系。
18.(1)76平方分米
(2)0.2立方分米
【分析】(1)求这个鱼缸至少用多少平方分米的玻璃,就是求这个无盖长方体鱼缸的表面积;根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出至少需要玻璃的面积。
(2)水面升高的部分就是12条金鱼的体积,根据长方体体积公式:长×宽×高,代入数据,求出12条金鱼的体积,再乘12,即可求出平均一条金鱼的体积。
【详解】(1)6×2+(6×4+4×2)×2
=12+(24+8)×2
=12+32×2
=12+64
=76(平方分米)
答:做这个鱼缸至少用了76平方分米的玻璃。
(2)6×2×(2.7-2.5)÷12
=12×0.2÷12
=2.4÷12
=0.2(立方分米)
答:鱼缸里的每条鱼的平均体重是0.2立方分米。
【点睛】利用长方体表面积公式、体积公式进行解答,关键熟记公式。
19.448平方厘米
【分析】这块长方形铁皮做成长方体的无盖盒子的长是32-4×2厘米,高是4厘米,无盖的盒子的容积是768毫升,根据根据长方体的体积公式:V=abh,代入数据求出无盖盒子的宽,由无盖盒子的宽加上2个4厘米即长方形的的宽,求出长方形的面积后减去四个小正方形的面积即为做这个盒子用的铁皮。
【详解】
(厘米)
(平方厘米)
答:做这个盒子用了448平方厘米的铁皮。
【点睛】解决本题关键是找出长方体的长宽高和原来长方形的长和宽之间的关系,求出长宽高即可解决问题。
20.(1)12升
(2)1500立方厘米
【分析】(1)长方体的容积=长×宽×高,据此解答。最后要换算单位。
(2)石头被水完全浸没,则石头的体积等于下降的水的体积。根据题意,下降的水的体积=容器的长×宽×水下降的高度,据此代入数据计算。
【详解】(1)30×25×16=12000(立方厘米)=12升
答:这个容器的容积是12升。
(2)30×25×2=1500(立方厘米)
答:这块石头的体积是1500立方厘米。
【点睛】本题考查长方体的容积和不规则物体的体积算法。理解“石头的体积等于下降的水的体积”是解题的关键。
21.24立方分米
【分析】把一块石块放入水中完全浸没,拿出石块后水面下降到1.8分米,那么下降水的体积就是石块的体积,根据长方体体积公式解答即可。
【详解】5×4×(3-1.8)
=20×1.2
=24(立方分米)
答:小石块的体积是24立方分米。
【点睛】此题主要考查求不规则物体的体积,即求下降水的体积,根据长方体的体积公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一单元长方体和正方体解答题过关练习(专项突破)-小学数学六年级上册苏教版
一、解答题
1.(1)小明家新买了一台洗衣机,请你帮他算一算,放置这台洗衣机要占多大面积?
(2)如果给洗衣机缝制一个布罩,至少需要多大面积的布料?(接缝处忽略不计,底面不需要)
2.惠民超市要做一个长5米、宽0.5米、高0.8米的玻璃柜台,至少需要多大面积的玻璃?
3.笑笑的房间长3.5米,宽3米,高3米,除去门窗4.5平方米,房间的墙壁和房顶都刷上涂料。每平方米用涂料0.28千克,至少需要涂料多少千克?
4.端午节这天,妈妈买了4盒绿豆糕,准备把这4盒绿豆糕包在一起,一盒绿豆糕的长、宽、高分别是15厘米、10厘米和4厘米,怎样包装最节省包装纸?至少需要包装纸多少平方厘米?(接口处不计)
5.下图是一个长方体灯笼罩的展开图。
(1)做一个灯笼罩需要多少平方分米的纸板?
(2)用木条扎一个这样的灯笼架,一共需要多少分米的木条?
6.爸爸想制作一种无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。做这个鱼缸至少需要玻璃多少平方分米?
7.有三个同样的长方体盒子,长10厘米,宽8厘米,高2厘米。现在要把这三个盒子包装在一起,最少需要多少平方厘米的包装纸?
8.一个无盖长方体纸箱的两个面如下。(每个小方格的边长代表1厘米)
(1)请你画出长方体纸箱其他的三个面。
(2)计算长方体纸箱的表面积。
9.母亲节到了,明明打算送一份礼物给妈妈(如图)。
(1)他要包装这个礼盒,至少需要多少平方厘米的彩纸?
(2)他用彩带捆扎礼盒,结头处的彩带长20厘米,至少需要多少厘米的彩带?
10.灯笼起源于2100多年前的西汉时期,是一种古老的汉族传统工艺品。每年的农历正月十五元宵节前后,人们都会挂起象征团圆意义的红灯笼。元宵节就要到了,笑笑想动手制作一个长方体灯笼的框架(如下图,单位:cm),至少需要多少厘米的木条?
11.如图,将此平面图沿虚线折叠出来是一座房屋的模型。制作这座房屋模型的屋顶,至少要用去多大面积的纸板?
12.用一些棱长为1cm的小正方体搭建成一个几何体,从两个角度观察所得的图形如下,那么这个几何体的体积最大是多少?
从上面看 从正面看
13.淘气家有一个长方体玻璃鱼缸,从里面量长8分米,宽4分米,高6分米,里面水深2.5分米。
(1)容器与水接触部分的面积是多少平方分米?
(2)如果全部装满水,能装多少升?
(3)在鱼缸中放入一个假山石(全部浸没在水中),结果水面上升1厘米,假山石的体积是多少立方分米?
14.某快递运货车的车厢是长方体,从里面量长5米、宽2.5米、高2米。它的容积是多少立方米?
15.用每条棱长都是1厘米的小正方体搭成一个每条棱长都是1分米的正方形体,需要多少个小正方体呢?
16.仔细观察下图,石块的体积是多少立方厘米?(水缸底面是正方形)
17.把一块不规则的铁块浸没到底面积是60平方厘米的长方体玻璃缸中,水面上升了0.6厘米,这块铁块的体积是多少?
18.爸爸买回来一个长6分米,宽2分米,高4分米的新鱼缸(无盖)。
(1)做这个鱼缸至少用了多少平方分米的玻璃?
(2)鱼缸里的每条鱼平均体积是多少?
19.把一块长32cm的长方形铁皮,在四角上剪去边长为4cm的小正方形,再做成无盖的盒子,盒子的容积是768mL。做这个盒子用了多少平方厘米的铁皮?
20.一个长方体玻璃容器长30厘米,宽25厘米,高16厘米。
(1)这个容器的容积是多少升?
(2)把一块石头放入这个盛有水的长方体容器中,石头被水完全浸没,水面高13厘米,把石头取出后,水面降低了2厘米,这块石头的体积是多少立方厘米?
21.一个长5分米、宽4分米、深3分米的长方体水缸里放入一个小石块,然后注满水(水完全浸没小石块),当取出小石块后,水面下降到1.8分米。小石块的体积是多少立方分米?
参考答案:
1.(1)3000平方厘米
(2)21700平方厘米
【分析】(1)观察图形可知,这台洗衣机是一个长方体,求它的占地面积,就是求长方体的底面积,根据长方形面积公式:面积=长×宽,代入数据,求出占地面积;
(2)求需要多大面积的布料,就是求这个长方体洗衣机去掉一个底面的5个面的面积和,根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】(1)60×50=3000(平方厘米)
答:放置这台洗衣机要占3000平方厘米大的面积。
(2)60×50+(60×85+50×85)×2
=3000+(5100+4250)×2
=3000+9350×2
=3000+18700
=21700(平方厘米)
答:至少需要21700平方厘米的布料。
【点睛】利用长方形面积公式和长方体表面积公式进行解答,关键熟记公式。
2.13.8平方米
【分析】求至少需要多大面积的玻璃,即求长方体的表面积,根据长方体表面积公式S=(ab+ah+bh)×2,代入数值计算即可。
【详解】(5×0.5+5×0.8+0.5×0.8)×2
=(2.5+4+0.4)×2
=6.9×2
=13.8(平方米)
答:至少需要13.8平方米面积的玻璃。
【点睛】本题考查长方体表面积公式的应用,关键是牢记公式。
3.12.6千克
【分析】根据题意,先根据长方体表面积公式,求出笑笑房间5个面的面积和,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出笑笑房间的表面积;再减去门窗的面积,就是要刷上涂料的面积,再乘0.28,就是至少需要涂料多少千克。
【详解】3.5×3+(3.5×3+3×3)×2-4.5
=10.5+(10.5+9)×2-4.5
=10.5+19.5×2-4.5
=10.5+39-4.5
=49.5-4.5
=45(平方米)
45×0.28=12.6(千克)
答:至少需要涂料12.6千克。
【点睛】利用长方体表面积公式进行解答,关键是熟记公式。
4.1100平方厘米
【分析】把这两个长方体盒子的15×10面相粘合,得到的大长方体的表面积最小,比原来两个盒子的表面积减少了2个最大的面,最节约包装纸,由此解答即可。
【详解】将15×10这个面重合摞在一起,拼成一个长15cm,宽10cm,高16cm的长方体最节约包装纸。
(15×10+15×16+16×10)×2
=(150+240+160)×2
=550×2
=1100(平方厘米)
答:至少需要包装纸1100平方厘米。
【点睛】抓住两个长方体拼组一个大长方体的方法:最大面相粘合,得到的大长方体的表面积最小;最小面相粘合,得到的大长方体的表面积最大。
5.(1)72平方分米
(2)44分米
【分析】(1)根据图形可知,长方体的长是6分米,宽是2分米,高是3分米,求做一个灯笼需要多少平方分米的纸板,就是求这个长方体的表面积,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)求需要多少分米的木条,就是求这个长方体的棱长总和,根据长方体棱长总和公式:(长+宽+高)×4,代入数据,即可解答。
【详解】(6×2+6×3+2×3)×2
=(12+18+6)×2
=(30+6)×2
=36×2
=72(平方分米)
答:做一个灯笼需要72平方分米纸板。
(2)(6+2+3)×4
=(8+3)×4
=11×4
=44(分米)
答:一共需要44分米的木条。
【点睛】利用长方体表面积公式、棱长总和公式进行解答;关键是确定长方体的长、宽和高的长度。
6.196平方分米
【分析】根据无盖长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解。
【详解】8×5+(8×6+5×6)×2
=40+(48+30)×2
=40+78×2
=40+156
=196(平方分米)
答:做这个鱼缸至少需要玻璃196平方分米。
【点睛】本题主要考查无盖长方体的表面积公式,熟练掌握它的公式并灵活运用。
7.376平方厘米
【分析】把三个长方体盒子叠在一起,有3种方式,重叠面积最大的叠法最省包装纸,即重叠底面时最省包装纸,据此解答。
【详解】因为三个面中底面最大,所以重合放在一起最省包装纸。
长方体的长是10厘米,宽是8厘米,高是2×3=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=(140+48)×2
=188×2
=376(平方厘米)
答:最少需要376平方厘米的包装纸。
【点睛】最大面重合,得到的长方体的表面积最小,最小面重合,得到的长方体表面积最大。
8.(1)见详解
(2)90平方厘米
【分析】(1)根据图形可知,长是6厘米,宽是3厘米的长方形是这个长方体的底面;再根据下面图形可知,长方体的高是4厘米;由此画出一个长是4厘米,宽是3厘米的长方形;再画出两个长是6厘米,宽是4厘米的长方形,就是这个长方体纸箱的其他的三个面;
(2)根据长方体的特征,长方体的长是6厘米,宽是3厘米,高是4厘米,根据无盖长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,即可解答。
【详解】(1)
(2)长方体的长是6厘米,宽是3厘米,高是4厘米。
表面积:6×3+(6×4+3×4)×2
=18+(24+12)×2
=18+36×2
=18+72
=90(平方厘米)
答:长方体的纸盒箱的表面积是90平方厘米。
【点睛】利用长方体的特征以及长方体表面积公式进行解答。
9.(1)1032平方厘米
(2)120厘米
【分析】(1)求包装这个礼盒需要多少平方厘米的彩纸,就是求这个礼盒的表面积,根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答;
(2)根据长方体的特征,它的12条棱分为互相平行(相对)的3组,每组4条棱的长度相等,由题意可知,彩带的长度就是长×2+宽×2+高×4+结头处彩带的长度,代入数据,即可解答。
【详解】(1)(12×18+12×10+18×10)×2
=(216+120+180)×2
=(336+180)×2
=516×2
=1032(平方厘米)
答:至少需要1032平方厘米的彩纸。
(2)12×2+18×2+10×4+20
=24+36+40+20
=60+40+20
=120(厘米)
答:至少需要120厘米的彩带。
【点睛】利用长方体的表面积公式,长方体的特征以及棱长总和公式的应用进行解答。
10.240厘米
【分析】根据题意,求制作这个长方体灯笼的框架,需要多少厘米的木条,就是求这个长方体的棱长总和,根据长方体棱长总和公式:棱长总和=(长+宽+高)×4,代入数据,即可解答。
【详解】(30+15+15)×4
=(45+15)×4
=60×4
=240(厘米)
答:至少需要240厘米的木条。
【点睛】利用长方体棱长总和的公式进行解答,关键是熟记公式。
11.32平方厘米
【分析】先将平面图折叠成立体图,判断出房屋模型中的屋顶面是哪个面,然后根据屋顶面形状,求出它的大小。在此模型中,屋顶面是由两个长方形面组成,所以运用长方形面积计算公式计算即可。
【详解】由分析可知:屋顶是由两个长为8厘米,宽为2厘米的长方形组成的。
8×2×2
=16×2
=32(平方厘米)
答:至少要用去32平方厘米的纸板。
【点睛】本题主要考查对图形的展开与折叠灵活运用。
12.7cm3
【分析】这个图形从正面看到5个小正方体,这5个小正方体可以分成3列,左右两列有2个正方体,中间一列有1个正方体。从上面看到两行,下面一行3个正方体,上面一行1个正方体,左对齐。下面一行的3个正方体是从正面看到的5个正方体中的3个。因为从正面看左面一列有2个正方体,所以上面一行的1个正方体表示这一列最多有2个正方体,则这个几何体最多有5+2=7个正方体,据此解答。
【详解】由分析得:
这个几何体最多有7个正方体,棱长为1cm的小正方体的体积是1cm3,则这个几何体的体积最大是7cm3。
【点睛】本题考查从不同方向观察物体,关键是明确这个几何体最多有几个小正方体,需要学生有较强的空间想象和推理能力。
13.(1)92平方分米;
(2)192升;
(3)3.2立方分米
【分析】(1)求容器与水接触部分的面积,实际上是求这个长方体容器4个侧面和1个底面的面积之和,可根据长方形的表面积公式:S=a×b+a×h×2+b×h×2,代入数据,即可求出长方体的表面积。
(2)求装满水的体积,实际上是求容器的容积,根据长方体的体积(容积)公式:V=abh,代入长宽高的数据,求出结果后,再进行单位换算即可。
(3)放入假山石后,假山的体积等于水面上升的的体积,这部分体积可以看作长为8分米、宽为4分米,高为1厘米的长方体的体积,注意计算前要换算高的单位,再利用长方体的体积公式:V=abh,代入即可求出假山石的体积。
【详解】(1)8×4+8×2.5×2+4×2.5×2
=32+40+20
=92(平方分米)
答:容器与水接触部分的面积是92平方分米。
(2)8×4×6=192(立方分米)
192立方分米=192升
答:如果全部装满水,能装192升。
(3)1厘米=0.1分米
8×4×0.1=3.2(立方分米)
答:假山石的体积是3.2立方分米。
【点睛】此题主要考查长方体表面积、体积的综合运用,熟记表面积和体积的公式,通过转化的数学思想,根据长方体的体积公式,求出不规则物体的体积。
14.25立方米
【分析】首先要清楚这道题是求长方体的容积,容积的计算方法和体积是一样的,就用长乘宽再乘高,列式计算即可解决。
【详解】5×2.5×2=25(立方米)
答:它的容积是25立方米。
【点睛】此题主要考查长方体容积的实际应用,长方体的容积计算公式:长方体的容积=长×宽×高。
15.1000个
【分析】1分米=10厘米,用小正方形撘成大正方体,可以摆10层,每层可以摆10行,10列。则每层有10×10=100个小正方体,一共有100×10=1000个小正方体。据此解答。
【详解】1分米=10厘米
10×10×10=1000(个)
答:需要1000个小正方体。
【点睛】解决本题时应先求出小正方体摆放层数,每层摆放个数,再求出小正方体个数,旨在考查学生的空间想象和推理能力。
16.900立方厘米
【分析】由题可知,水面上升的体积等于石块的体积,根据长方体的体积公式:V=abh,代入数据计算即可。
【详解】
=225×4
=900(立方厘米)
答:石块的体积是900立方厘米。
【点睛】本题的关键是理解石块的体积等于水面上升的体积,还可以用上升后的体积减去上升前的体积,也可以解答。
17.36立方厘米
【分析】根据题意可知,铁块的体积等于水面上升部分的体积;根据长方体体积公式:底面积×高,代入数据,即可解答。
【详解】60×0.6=36(立方厘米)
答:这块铁块的体积是立方厘米。
【点睛】本题考查不规则物体体积的求法,关键明确铁块的体积与水面上升部分之间的关系。
18.(1)76平方分米
(2)0.2立方分米
【分析】(1)求这个鱼缸至少用多少平方分米的玻璃,就是求这个无盖长方体鱼缸的表面积;根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出至少需要玻璃的面积。
(2)水面升高的部分就是12条金鱼的体积,根据长方体体积公式:长×宽×高,代入数据,求出12条金鱼的体积,再乘12,即可求出平均一条金鱼的体积。
【详解】(1)6×2+(6×4+4×2)×2
=12+(24+8)×2
=12+32×2
=12+64
=76(平方分米)
答:做这个鱼缸至少用了76平方分米的玻璃。
(2)6×2×(2.7-2.5)÷12
=12×0.2÷12
=2.4÷12
=0.2(立方分米)
答:鱼缸里的每条鱼的平均体重是0.2立方分米。
【点睛】利用长方体表面积公式、体积公式进行解答,关键熟记公式。
19.448平方厘米
【分析】这块长方形铁皮做成长方体的无盖盒子的长是32-4×2厘米,高是4厘米,无盖的盒子的容积是768毫升,根据根据长方体的体积公式:V=abh,代入数据求出无盖盒子的宽,由无盖盒子的宽加上2个4厘米即长方形的的宽,求出长方形的面积后减去四个小正方形的面积即为做这个盒子用的铁皮。
【详解】
(厘米)
(平方厘米)
答:做这个盒子用了448平方厘米的铁皮。
【点睛】解决本题关键是找出长方体的长宽高和原来长方形的长和宽之间的关系,求出长宽高即可解决问题。
20.(1)12升
(2)1500立方厘米
【分析】(1)长方体的容积=长×宽×高,据此解答。最后要换算单位。
(2)石头被水完全浸没,则石头的体积等于下降的水的体积。根据题意,下降的水的体积=容器的长×宽×水下降的高度,据此代入数据计算。
【详解】(1)30×25×16=12000(立方厘米)=12升
答:这个容器的容积是12升。
(2)30×25×2=1500(立方厘米)
答:这块石头的体积是1500立方厘米。
【点睛】本题考查长方体的容积和不规则物体的体积算法。理解“石头的体积等于下降的水的体积”是解题的关键。
21.24立方分米
【分析】把一块石块放入水中完全浸没,拿出石块后水面下降到1.8分米,那么下降水的体积就是石块的体积,根据长方体体积公式解答即可。
【详解】5×4×(3-1.8)
=20×1.2
=24(立方分米)
答:小石块的体积是24立方分米。
【点睛】此题主要考查求不规则物体的体积,即求下降水的体积,根据长方体的体积公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
