七年级相交线复习教案[下学期]
文档属性
| 名称 | 七年级相交线复习教案[下学期] | 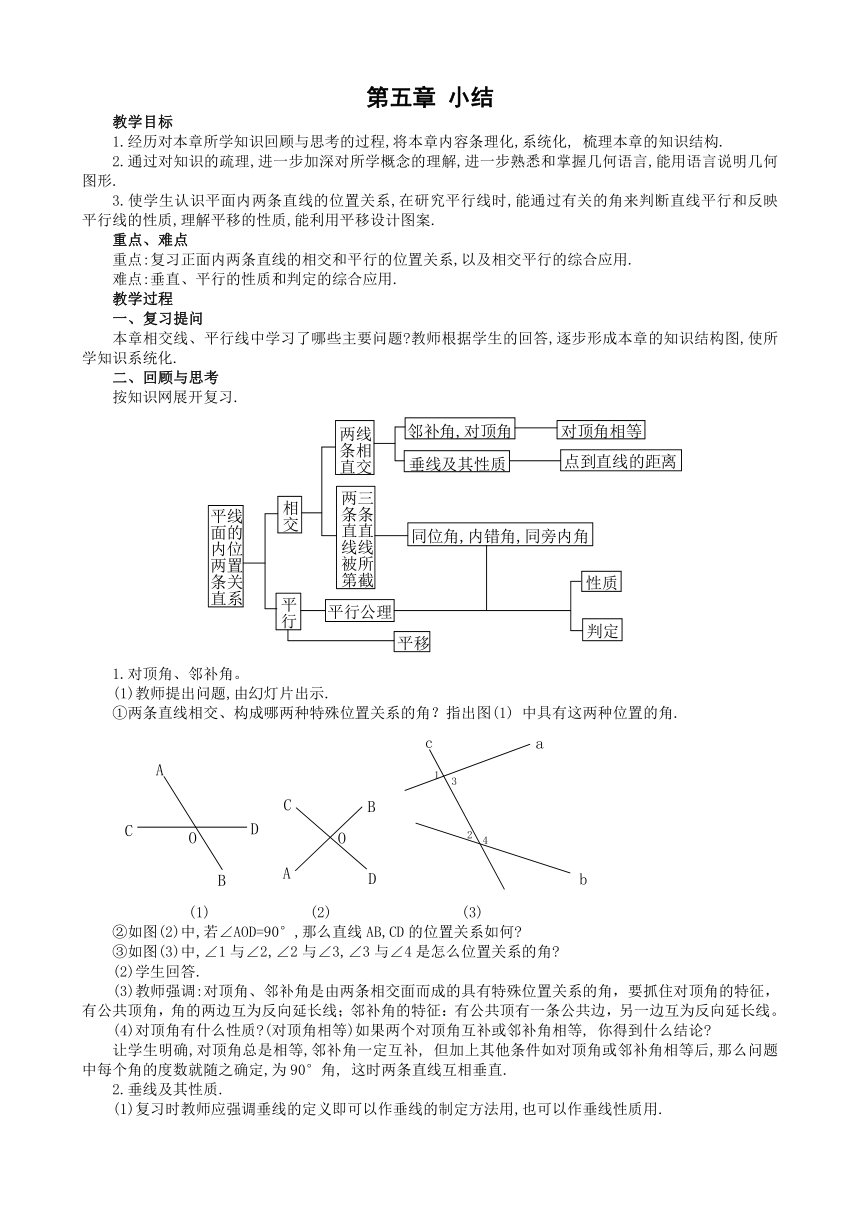 | |
| 格式 | rar | ||
| 文件大小 | 26.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-04 12:33:00 | ||
图片预览

文档简介
第五章 小结
教学目标
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.毛
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
重点、难点
重点:复习正面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
难点:垂直、平行的性质和判定的综合应用.
教学过程
一、复习提问
本章相交线、平行线中学习了哪些主要问题 教师根据学生的回答,逐步形成本章的知识结构图,使所学知识系统化.
二、回顾与思考
按知识网展开复习.
1.对顶角、邻补角。
(1)教师提出问题,由幻灯片出示.
①两条直线相交、构成哪两种特殊位置关系的角?指出图(1) 中具有这两种位置的角.
(1) (2) (3)
②如图(2)中,若∠AOD=90°,那么直线AB,CD的位置关系如何
③如图(3)中,∠1与∠2,∠2与∠3,∠3与∠4是怎么位置关系的角
(2)学生回答.
(3)教师强调:对顶角、邻补角是由两条相交面而成的具有特殊位置关系的角,要抓住对顶角的特征,有公共顶角,角的两边互为反向延长线;邻补角的特征:有公共顶有一条公共边,另一边互为反向延长线。
(4)对顶角有什么性质 (对顶角相等)如果两个对顶角互补或邻补角相等, 你得到什么结论
让学生明确,对顶角总是相等,邻补角一定互补, 但加上其他条件如对顶角或邻补角相等后,那么问题中每个角的度数就随之确定,为90°角, 这时两条直线互相垂直.
2.垂线及其性质.
(1)复习时教师应强调垂线的定义即可以作垂线的制定方法用,也可以作垂线性质用.
作判定用时写成:如图(2),因为∠AOD=90°,所以AB⊥CD, 这是一个角的“数”到两直线垂直的“形”的判断。
作为性质用时写成:如图(2),因为AB⊥CD,所以∠AOD=90°。这是由“形”到“数”的说理。
(2)如图(4),直线AB、CD、EF相交于点O,CD⊥EF,∠1=35°,求∠2的度数.
(4) (5) (6)
鼓励学生用不同方法求解.
(3)垂线性质1和性质2.
让学生叙述垂线的性质,懂得分清这两个命题的题设和结论,垂线性质一说得过一点已知直线的垂线存在并且唯一的.
学生思考:
①请回忆一下后体育课测跳远成绩时,教师是怎样测量的
如图(5),AB⊥L,BC⊥L,B为重足,那么A、B、C三点在同一②条直线上吗 为什么
③点到直线的距离、两条平行线的距离.
初中阶级学习了三种距离,即是距离,就要懂得的共同点:距离都是线段的长度,又要懂得区别:两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是某条直线上的一点到另一点平行线的距离.
学生练习:①如图(6),四边形ABCD,AD∥BC,AB∥CD,过A作AE⊥BC,过A作AF⊥CD,垂足分别是E、F,量出点A到BC的距离和AB、CD平行线间的距离.
②请归纳一下与垂直有关的知识中,有哪些重要结论
如垂线的性质1、2,又如两种直线都垂直于第三条直线,这两条直线平行, 一条直线与平行线中一条垂直,也与另一条垂直……
3.同位角、内错角、同旁内角.
只要求学生从图形中找出同位角,内错角,同旁内角.
练习:如图(7),找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角.
(7)
4.平行线判定与性质
(1)怎样判别两条直线是否平行.
(2)平行线有什么特征
(3)对比平行线的性质和直线平行的条件,它们有什么异同
(4)为什么研究平面内两直线的位置关系总是与角联系起来 围绕这些问题展开讨论,交流.
教师使学生进一步明确: 平行线的判定也是由“数”即角与角的关系到“形”的判断,而性质则是“形”到“数”的说理,在研究两条直线的垂直或平行时共同点是把研究它们的位置关系转化为研究角或角之间的关系。
学生练习:①填空:如图(8),当_______时,a∥c,理由是________;当______时, b∥c,理由是_________;当a∥b,b∥c时,______∥______,理由是_________.
(8) (9) (10)
②如图(9),AB∥CD,∠A=∠C,试判断AD与BC的位置关系 为什么
教师根据学生情况酌情给予引导.
5.关于平移,让学生思考:
(1)图形平移时,连接对应点有什么关系
(2)如何确定图形平移的方向和平移的距离
(3)你能用平移设计一些图案吗
练习:如图(10),平移四边形ABCD,使点B移动到点B′,画出平移后的四边形A′B′C′D′.
三、作业
课本P39.1~8.
教学目标
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.毛
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
重点、难点
重点:复习正面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
难点:垂直、平行的性质和判定的综合应用.
教学过程
一、复习提问
本章相交线、平行线中学习了哪些主要问题 教师根据学生的回答,逐步形成本章的知识结构图,使所学知识系统化.
二、回顾与思考
按知识网展开复习.
1.对顶角、邻补角。
(1)教师提出问题,由幻灯片出示.
①两条直线相交、构成哪两种特殊位置关系的角?指出图(1) 中具有这两种位置的角.
(1) (2) (3)
②如图(2)中,若∠AOD=90°,那么直线AB,CD的位置关系如何
③如图(3)中,∠1与∠2,∠2与∠3,∠3与∠4是怎么位置关系的角
(2)学生回答.
(3)教师强调:对顶角、邻补角是由两条相交面而成的具有特殊位置关系的角,要抓住对顶角的特征,有公共顶角,角的两边互为反向延长线;邻补角的特征:有公共顶有一条公共边,另一边互为反向延长线。
(4)对顶角有什么性质 (对顶角相等)如果两个对顶角互补或邻补角相等, 你得到什么结论
让学生明确,对顶角总是相等,邻补角一定互补, 但加上其他条件如对顶角或邻补角相等后,那么问题中每个角的度数就随之确定,为90°角, 这时两条直线互相垂直.
2.垂线及其性质.
(1)复习时教师应强调垂线的定义即可以作垂线的制定方法用,也可以作垂线性质用.
作判定用时写成:如图(2),因为∠AOD=90°,所以AB⊥CD, 这是一个角的“数”到两直线垂直的“形”的判断。
作为性质用时写成:如图(2),因为AB⊥CD,所以∠AOD=90°。这是由“形”到“数”的说理。
(2)如图(4),直线AB、CD、EF相交于点O,CD⊥EF,∠1=35°,求∠2的度数.
(4) (5) (6)
鼓励学生用不同方法求解.
(3)垂线性质1和性质2.
让学生叙述垂线的性质,懂得分清这两个命题的题设和结论,垂线性质一说得过一点已知直线的垂线存在并且唯一的.
学生思考:
①请回忆一下后体育课测跳远成绩时,教师是怎样测量的
如图(5),AB⊥L,BC⊥L,B为重足,那么A、B、C三点在同一②条直线上吗 为什么
③点到直线的距离、两条平行线的距离.
初中阶级学习了三种距离,即是距离,就要懂得的共同点:距离都是线段的长度,又要懂得区别:两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度, 平行线间的距离是某条直线上的一点到另一点平行线的距离.
学生练习:①如图(6),四边形ABCD,AD∥BC,AB∥CD,过A作AE⊥BC,过A作AF⊥CD,垂足分别是E、F,量出点A到BC的距离和AB、CD平行线间的距离.
②请归纳一下与垂直有关的知识中,有哪些重要结论
如垂线的性质1、2,又如两种直线都垂直于第三条直线,这两条直线平行, 一条直线与平行线中一条垂直,也与另一条垂直……
3.同位角、内错角、同旁内角.
只要求学生从图形中找出同位角,内错角,同旁内角.
练习:如图(7),找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角.
(7)
4.平行线判定与性质
(1)怎样判别两条直线是否平行.
(2)平行线有什么特征
(3)对比平行线的性质和直线平行的条件,它们有什么异同
(4)为什么研究平面内两直线的位置关系总是与角联系起来 围绕这些问题展开讨论,交流.
教师使学生进一步明确: 平行线的判定也是由“数”即角与角的关系到“形”的判断,而性质则是“形”到“数”的说理,在研究两条直线的垂直或平行时共同点是把研究它们的位置关系转化为研究角或角之间的关系。
学生练习:①填空:如图(8),当_______时,a∥c,理由是________;当______时, b∥c,理由是_________;当a∥b,b∥c时,______∥______,理由是_________.
(8) (9) (10)
②如图(9),AB∥CD,∠A=∠C,试判断AD与BC的位置关系 为什么
教师根据学生情况酌情给予引导.
5.关于平移,让学生思考:
(1)图形平移时,连接对应点有什么关系
(2)如何确定图形平移的方向和平移的距离
(3)你能用平移设计一些图案吗
练习:如图(10),平移四边形ABCD,使点B移动到点B′,画出平移后的四边形A′B′C′D′.
三、作业
课本P39.1~8.
