2022-2023学年青岛版九年级数学上册 3.4.3直线与圆的位置关系 (第3课时) 课件(共20张PPT)
文档属性
| 名称 | 2022-2023学年青岛版九年级数学上册 3.4.3直线与圆的位置关系 (第3课时) 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 284.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 20:34:41 | ||
图片预览



文档简介
(共20张PPT)
第3课时 切线的性质
3.4 直线与圆的位置关系
复习引入:
切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
学习目标
1、探索切线的性质;
2、通过应用切线的性质,提高推理判断能力.
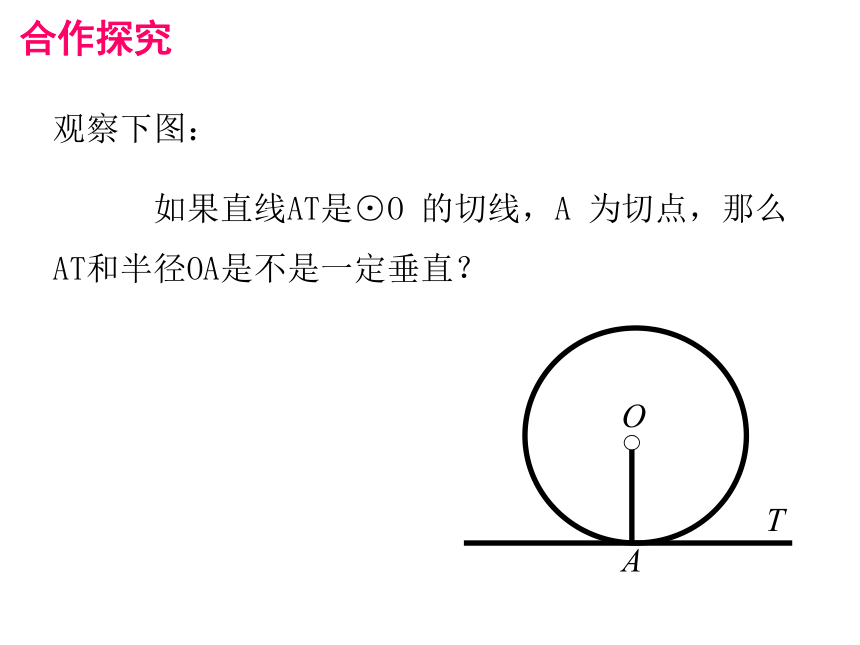
观察下图:
如果直线AT是⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
合作探究
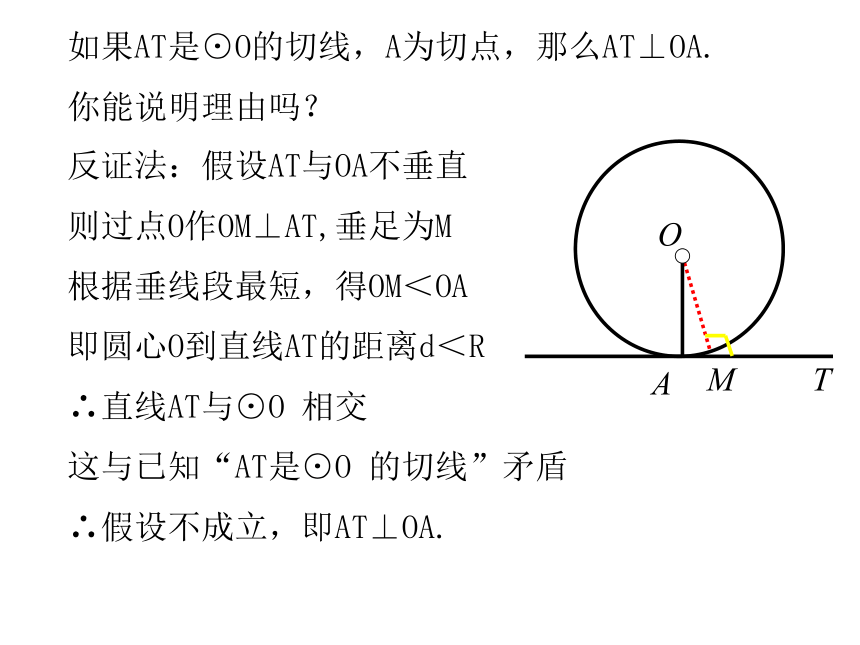
如果AT是⊙O的切线,A为切点,那么AT⊥OA.
你能说明理由吗?
A
T
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT与⊙O 相交
这与已知“AT是⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA.
O
O
A
T
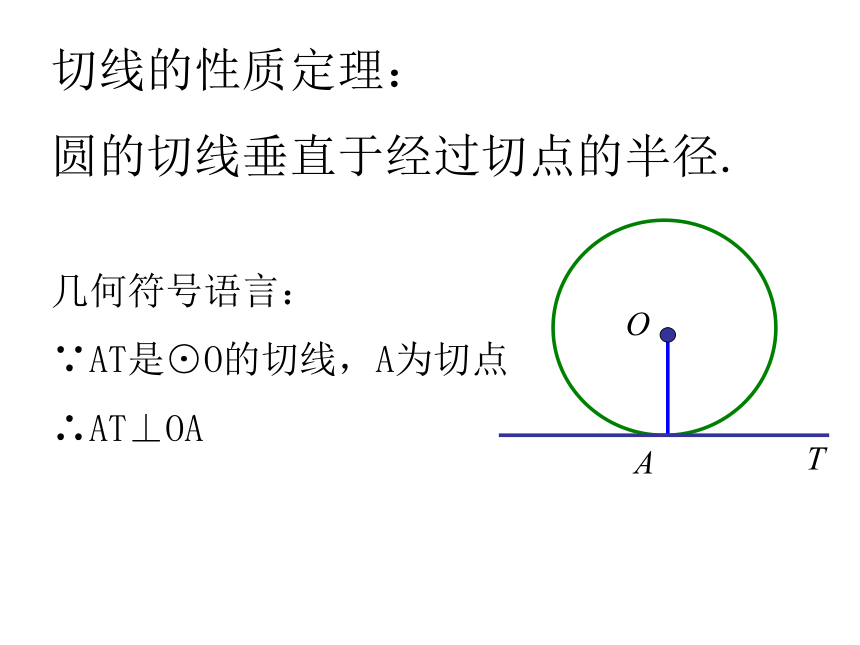
切线的性质定理:
圆的切线垂直于经过切点的半径.
几何符号语言:
∵AT是⊙O的切线,A为切点
∴AT⊥OA
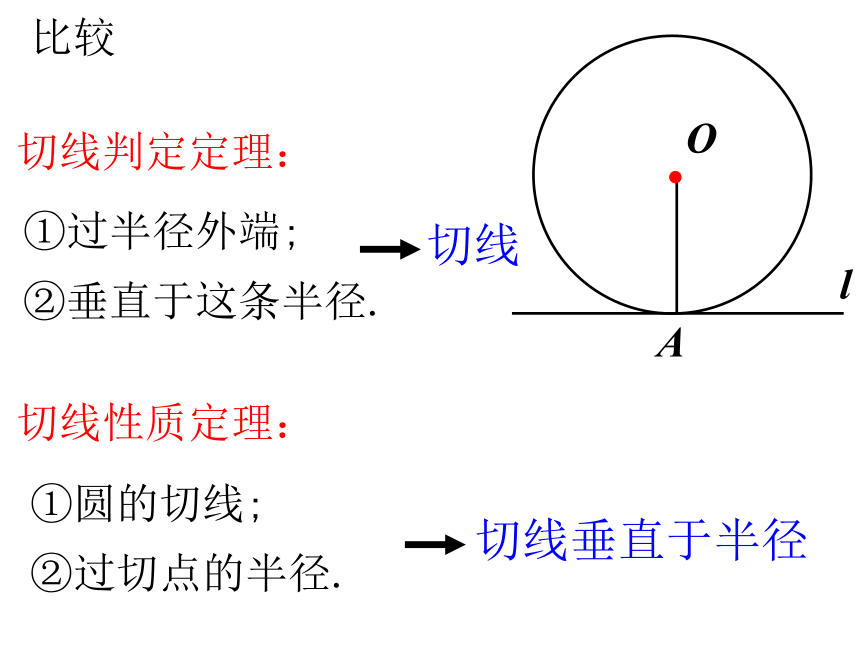
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
O
A
l
比较
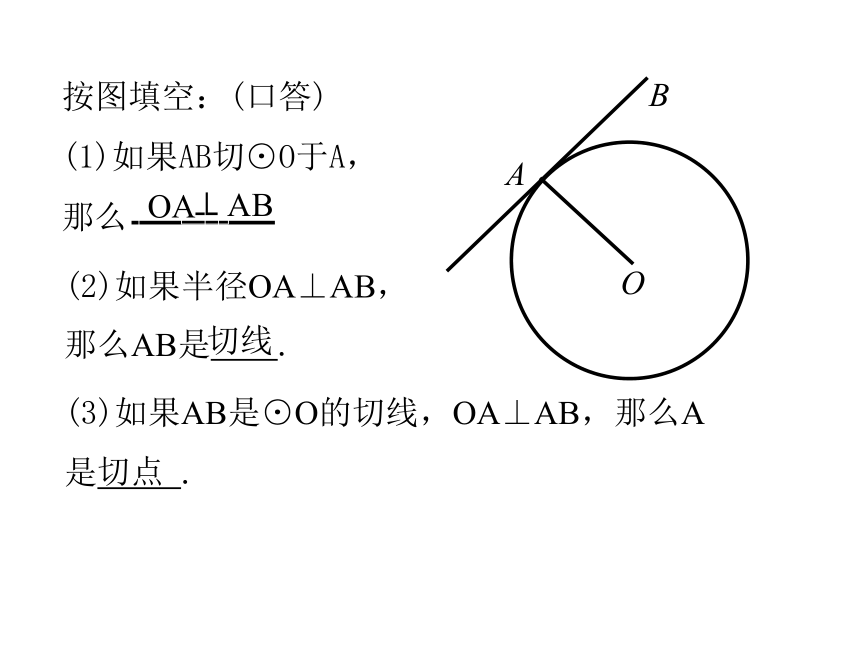
按图填空:(口答)
(1)如果AB切⊙O于A,
那么
A
O
B
(2)如果半径OA⊥AB,那么AB是 .
切点
(3)如果AB是⊙O的切线,OA⊥AB,那么A
是 .
⊥
OA
AB.
切线
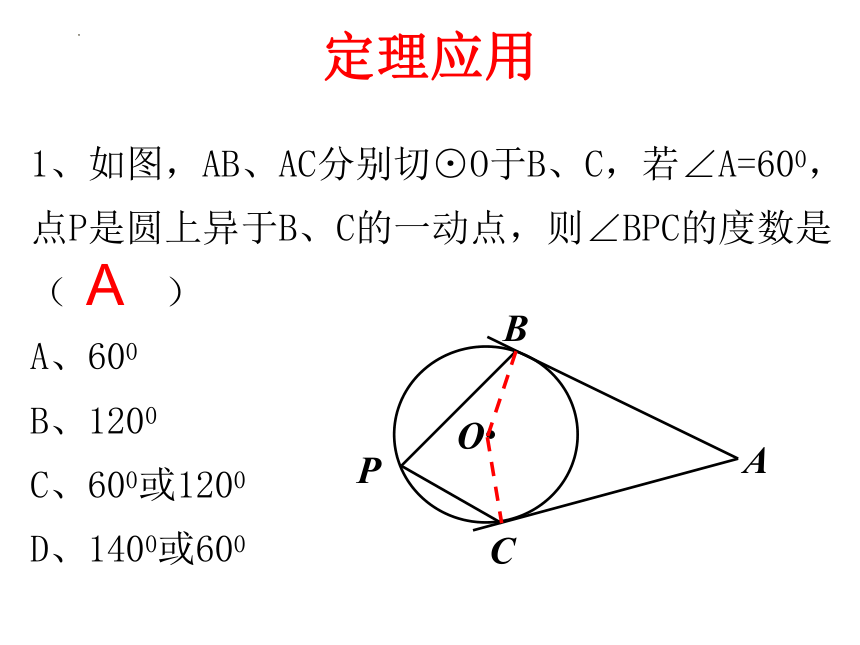
1、如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A、600
B、1200
C、600或1200
D、1400或600
B
P
C
A
O
定理应用
A
2、如图, ⊙O与PB相切,切点为点B,PB=4,PA=2,则⊙O的半径多少?
定理应用
3
例题讲解
例3 A,B,C是⊙O 上的三点,经过点 A,点 B 分别作⊙O 的切线,两切线相交于点 P,如果∠P = 42°,求∠ACB 的度数.
C ′
例3:A,B,C是⊙O上三点,经过点A,点B分别作⊙O的切线,两切线相交于点P,如果∠P=42°,求∠ACB的度数.
(2)如图,当点C在劣弧AB上时,
在优弧AmB上任取一点C′,连接AC′,BC′
由(1)知,∠AC′B=69°,
在圆内接四边形ACBC′中
∵∠ACB+∠AC′B=180°
∴∠ACB=180°-∠AC′B=180°-69°=111°.
归纳:切线的性质及辅助线的作法
1.性质:
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于圆的半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点.
(5)经过切点且垂直于切线的直线必过圆心.
2.辅助线的作法:
见切点,连半径,得垂直
1、已知:如图,AB是⊙O的弦,AC切⊙O于点A,且∠BAC=54°,求∠OBA的度数.
巩固练习
36°
2. 如图,△ABC 内接于⊙O,AB 为直径,直线 BE 切⊙O 于点 B . 求证:∠A =∠CBE .
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
1.切线性质:
2.能运用切线性质定理进行计算与证明
3.掌握常见的关于切线辅助线作法
课堂小结
1.如图,∠MAB=30°,P为AB上的点,且AP=6,☉P与AM相
切,则圆P的半径为__.
达标检测
3
2
1
O
B
A
C
D
2.如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
作业
必做题:课本96页练习2
选做题:课本100页12题
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,试判断△AED的形状,并说明理由.
【解析】△AED为直角三角形,理由如下连接OE.
∵ DE是⊙O的切线,
∴OE⊥DE,∠OED=90°,
即∠OEA+∠AED=90°.
又AE平分∠BAC,∴∠OAE=∠EAD.
∵OA=OE,∴∠OAE=∠OEA.
∴∠AED+∠EAD=90°,
∴∠ADE=90°,
∴△AED为直角三角形.
第3课时 切线的性质
3.4 直线与圆的位置关系
复习引入:
切线的判定定理?
经过半径的外端并且垂直于这条半径的直线是
圆的切线.
学习目标
1、探索切线的性质;
2、通过应用切线的性质,提高推理判断能力.
观察下图:
如果直线AT是⊙O 的切线,A 为切点,那么 AT和半径OA是不是一定垂直?
A
T
O
合作探究
如果AT是⊙O的切线,A为切点,那么AT⊥OA.
你能说明理由吗?
A
T
O
M
反证法:假设AT与OA不垂直
则过点O作OM⊥AT,垂足为M
根据垂线段最短,得OM<OA
即圆心O到直线AT的距离d<R
∴直线AT与⊙O 相交
这与已知“AT是⊙O 的切线”矛盾
∴假设不成立,即AT⊥OA.
O
O
A
T
切线的性质定理:
圆的切线垂直于经过切点的半径.
几何符号语言:
∵AT是⊙O的切线,A为切点
∴AT⊥OA
①过半径外端;
②垂直于这条半径.
切线
①圆的切线;
②过切点的半径.
切线垂直于半径
切线判定定理:
切线性质定理:
O
A
l
比较
按图填空:(口答)
(1)如果AB切⊙O于A,
那么
A
O
B
(2)如果半径OA⊥AB,那么AB是 .
切点
(3)如果AB是⊙O的切线,OA⊥AB,那么A
是 .
⊥
OA
AB.
切线
1、如图,AB、AC分别切⊙O于B、C,若∠A=600,点P是圆上异于B、C的一动点,则∠BPC的度数是( )
A、600
B、1200
C、600或1200
D、1400或600
B
P
C
A
O
定理应用
A
2、如图, ⊙O与PB相切,切点为点B,PB=4,PA=2,则⊙O的半径多少?
定理应用
3
例题讲解
例3 A,B,C是⊙O 上的三点,经过点 A,点 B 分别作⊙O 的切线,两切线相交于点 P,如果∠P = 42°,求∠ACB 的度数.
C ′
例3:A,B,C是⊙O上三点,经过点A,点B分别作⊙O的切线,两切线相交于点P,如果∠P=42°,求∠ACB的度数.
(2)如图,当点C在劣弧AB上时,
在优弧AmB上任取一点C′,连接AC′,BC′
由(1)知,∠AC′B=69°,
在圆内接四边形ACBC′中
∵∠ACB+∠AC′B=180°
∴∠ACB=180°-∠AC′B=180°-69°=111°.
归纳:切线的性质及辅助线的作法
1.性质:
(1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于圆的半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点.
(5)经过切点且垂直于切线的直线必过圆心.
2.辅助线的作法:
见切点,连半径,得垂直
1、已知:如图,AB是⊙O的弦,AC切⊙O于点A,且∠BAC=54°,求∠OBA的度数.
巩固练习
36°
2. 如图,△ABC 内接于⊙O,AB 为直径,直线 BE 切⊙O 于点 B . 求证:∠A =∠CBE .
①切线和圆有且只有一个公共点
③圆的切线垂直于经过切点的半径
②切线和圆心的距离等于半径
1.切线性质:
2.能运用切线性质定理进行计算与证明
3.掌握常见的关于切线辅助线作法
课堂小结
1.如图,∠MAB=30°,P为AB上的点,且AP=6,☉P与AM相
切,则圆P的半径为__.
达标检测
3
2
1
O
B
A
C
D
2.如图,AB为⊙O的直径, C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
作业
必做题:课本96页练习2
选做题:课本100页12题
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E作⊙O的切线交AC于点D,试判断△AED的形状,并说明理由.
【解析】△AED为直角三角形,理由如下连接OE.
∵ DE是⊙O的切线,
∴OE⊥DE,∠OED=90°,
即∠OEA+∠AED=90°.
又AE平分∠BAC,∴∠OAE=∠EAD.
∵OA=OE,∴∠OAE=∠OEA.
∴∠AED+∠EAD=90°,
∴∠ADE=90°,
∴△AED为直角三角形.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
