2022-2023学年青岛版九年级数学上册 3.5 三角形的内切圆 课件(共19张PPT)
文档属性
| 名称 | 2022-2023学年青岛版九年级数学上册 3.5 三角形的内切圆 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 20:43:25 | ||
图片预览



文档简介
(共19张PPT)
C
O
A
B
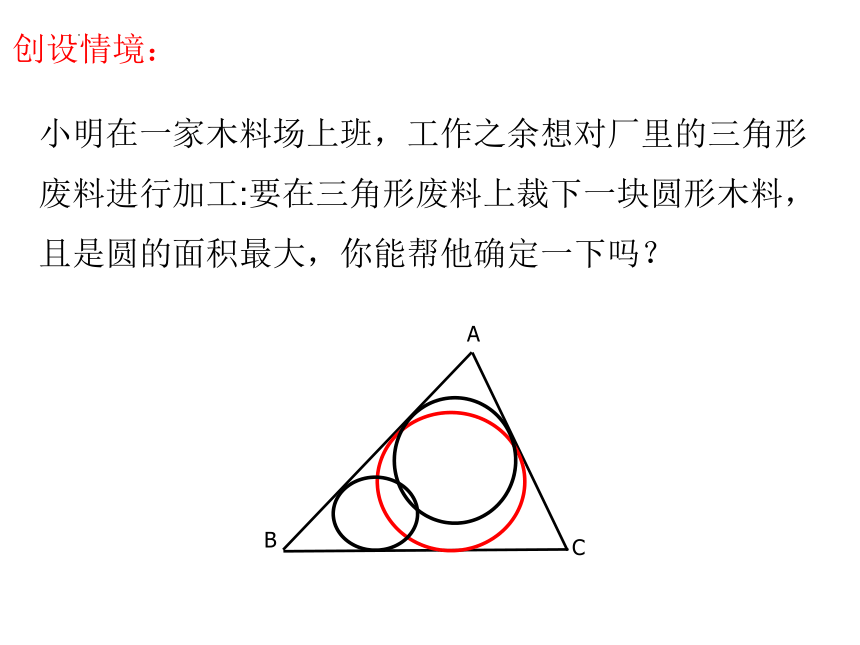
复习回顾
1.什么叫三角形的外接圆.
2.什么叫外心
3.什么叫内接三角形
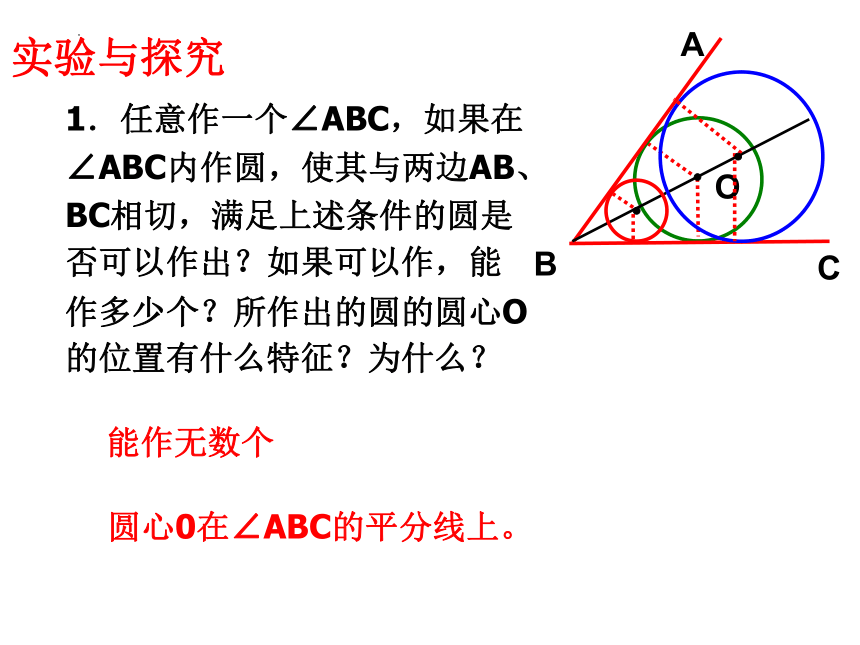
创设情境:
小明在一家木料场上班,工作之余想对厂里的三角形
废料进行加工:要在三角形废料上裁下一块圆形木料,
且是圆的面积最大,你能帮他确定一下吗?
A
B
C
3.5 三角形的内切圆
九年级数学(上)第三章: 对圆的进一步认识
学习目标
1.了解三角形的内切圆、三角形的内心、圆的外
切三角形的概念;
2.了解三角形内心的性质,并会进行有关的计算.
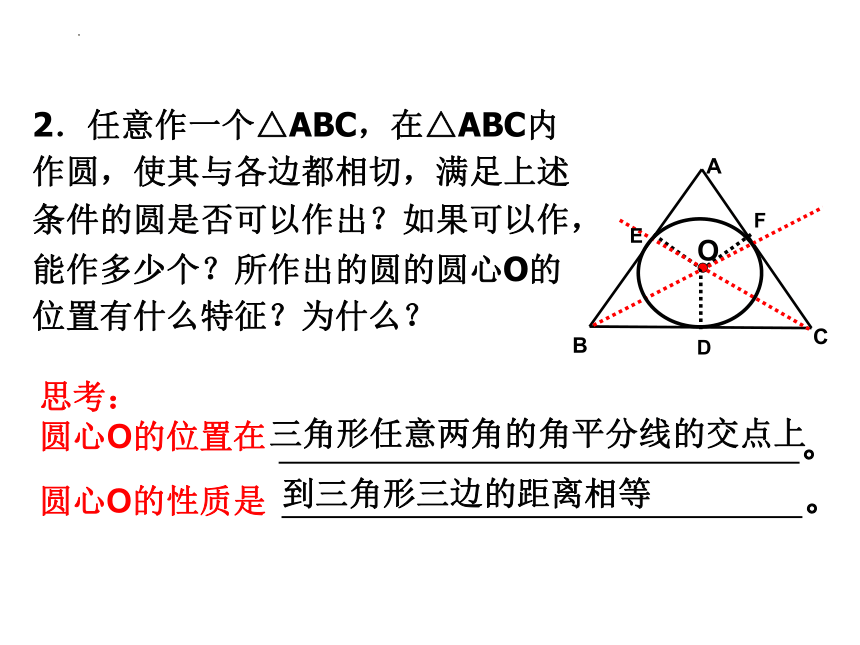
1.任意作一个∠ABC,如果在∠ABC内作圆,使其与两边AB、BC相切,满足上述条件的圆是否可以作出?如果可以作,能作多少个?所作出的圆的圆心O的位置有什么特征?为什么?
圆心0在∠ABC的平分线上。
O
A
B
C
能作无数个
实验与探究
2.任意作一个△ABC,在△ABC内作圆,使其与各边都相切,满足上述条件的圆是否可以作出?如果可以作,能作多少个?所作出的圆的圆心O的位置有什么特征?为什么?
思考:
圆心O的位置在
O
A
B
C
D
F
E
三角形任意两角的角平分线的交点上
。
圆心O的性质是
。
到三角形三边的距离相等
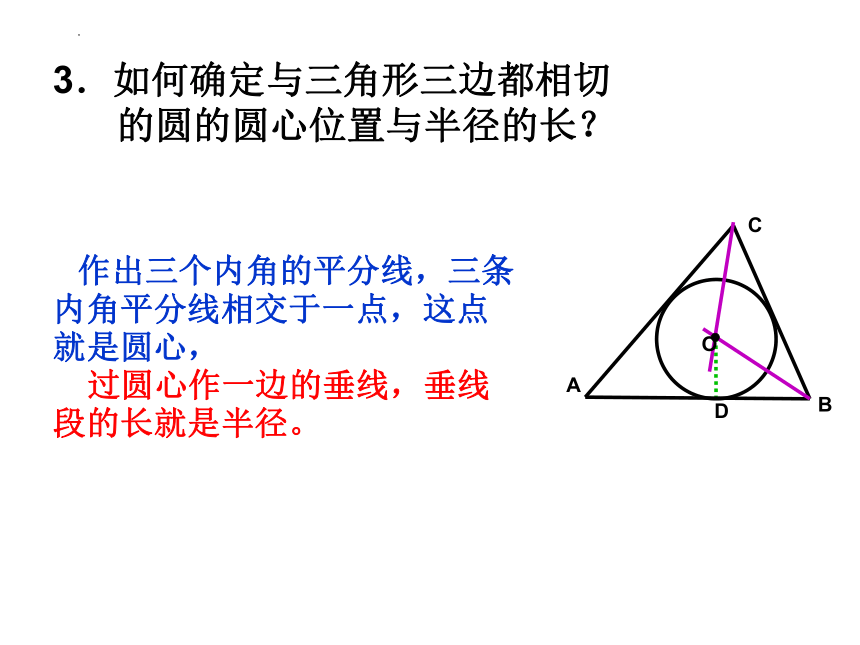
作出三个内角的平分线,三条内角平分线相交于一点,这点就是圆心,
过圆心作一边的垂线,垂线段的长就是半径。
O
C
A
B
D
3.如何确定与三角形三边都相切
的圆的圆心位置与半径的长?
A
B
C
M
已知: △ABC(如图).
求作:和△ABC的各边都相切的圆.
作法:1. 作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
N
I
D
2. 过点I作ID⊥BC,垂足为点D.
3. 以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆.
4.怎样用尺规作一个圆,使它与△ABC的各边都相切?
三角形与圆的位置关系
与三角形各边都相切的圆叫做 .
这个三角形叫做 .
内切圆的圆心叫做 .
三角形的内心是
.
A
B
C
●
I
三角形的内切圆
圆的外切三角形
三角形的内心
三角形三条角平分线的交点
名称 图形 确定方法 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
垂直平分线
的交点
1.OA=OB=OC
2.外心不一定在三角形的外部.
1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
o
A
B
C
O
A
B
C
三角形三条
角平分线的
交点
1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的 交点.
外接
内接
外心
三边垂直平分线
2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点.
外切
内切
内
三条角平分线
A
B
C
O
.
图1
I
D
E
F
.
图2
按图填空
解:
∵点I是△ABC的内心,
∴ (∠1+ ∠2)
例1 如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数.
A
B
C
I
)
1
(
2
4
(
∴ ∠1= ∠ABC.
3
)
同理 ∠2= ∠ACB.
= ( ∠ABC+ )
= ( 180° - ∠A )
= ( 180° - 68° )
= 56°
∠ACB
∴∠BIC= 180° - (∠1+ ∠2)
= 180°- 56°= 124°
如图,在△ABC中,∠A=68°,点I分别是两外角(图一)、一内角一外角(图二)的角平分线交点,
求∠BIC的度数.
图一
图二
∠I=56°
∠I=34°
68°
68°
2
1
3
4
2
1
4
3
挑战自我
1.已知△ABC的三边长分别为a,b,c,它的内切圆
半径为r,你会求△ABC的面积吗?
2.已知Rt△ABC的两直角边和斜边分别为a,b,C,你会求它的内切圆半径吗?
A
B
C
O●
┓
●
C
A
B
┐
●
┓
┓
.
A
B
C
a
b
c
r
r =
a+b-c
2
r
O
已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,求其内切圆O的半径长.
E
D
r
r
a-r
a-r
b-r+a-r=c
b-r
F
b-r
1. 通过类比三角形的外接圆与圆的内接三角形概念得出三角形的内切圆、圆的外切三角形概念.
2. 利用三角形内心的性质解题时,要注意整体思想和化整为零思想的运用.
课堂小结:
1.三角形的内切圆能作____个,圆的外切
三角形有_____ 个,三角形的内心在圆
的_______.
2.如图,O是△ABC的内心,则
(1)OA平分∠______, OB平分
∠______,OC平分∠______.
(2)若∠BAC=100°,则∠BOC=______.
1
无数
内部
C
O
B
A
BAC
140
ABC
ACB
3.直角三角形的两直角边分别5cm,12cm .则其内切圆的半径______。
.
A
B
C
O
2cm
达标检测
必做题:课本103页练习第2题
选做题:课本104页练习第5题
(2)若∠A=80 °,则∠BOC = 度.
(3)若∠BOC=100 °,则∠A = 度.
解:
130
20
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(20°+ 35 °) =125 °.
例1 如图,在△ABC中,点O是内心, (1)若∠ABC=40°, ∠ACB=70°,求∠BOC的度数.
A
B
C
O
)
1
(
3
4
(
∴ ∠1= ∠2= ∠ABC= ×40°= 20°.
2
)
同理 ∠3= ∠4= ∠ACB= ×70° =35 °.
C
O
A
B
复习回顾
1.什么叫三角形的外接圆.
2.什么叫外心
3.什么叫内接三角形
创设情境:
小明在一家木料场上班,工作之余想对厂里的三角形
废料进行加工:要在三角形废料上裁下一块圆形木料,
且是圆的面积最大,你能帮他确定一下吗?
A
B
C
3.5 三角形的内切圆
九年级数学(上)第三章: 对圆的进一步认识
学习目标
1.了解三角形的内切圆、三角形的内心、圆的外
切三角形的概念;
2.了解三角形内心的性质,并会进行有关的计算.
1.任意作一个∠ABC,如果在∠ABC内作圆,使其与两边AB、BC相切,满足上述条件的圆是否可以作出?如果可以作,能作多少个?所作出的圆的圆心O的位置有什么特征?为什么?
圆心0在∠ABC的平分线上。
O
A
B
C
能作无数个
实验与探究
2.任意作一个△ABC,在△ABC内作圆,使其与各边都相切,满足上述条件的圆是否可以作出?如果可以作,能作多少个?所作出的圆的圆心O的位置有什么特征?为什么?
思考:
圆心O的位置在
O
A
B
C
D
F
E
三角形任意两角的角平分线的交点上
。
圆心O的性质是
。
到三角形三边的距离相等
作出三个内角的平分线,三条内角平分线相交于一点,这点就是圆心,
过圆心作一边的垂线,垂线段的长就是半径。
O
C
A
B
D
3.如何确定与三角形三边都相切
的圆的圆心位置与半径的长?
A
B
C
M
已知: △ABC(如图).
求作:和△ABC的各边都相切的圆.
作法:1. 作∠ABC、 ∠ACB的平分线BM和CN,交点为I.
N
I
D
2. 过点I作ID⊥BC,垂足为点D.
3. 以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆.
4.怎样用尺规作一个圆,使它与△ABC的各边都相切?
三角形与圆的位置关系
与三角形各边都相切的圆叫做 .
这个三角形叫做 .
内切圆的圆心叫做 .
三角形的内心是
.
A
B
C
●
I
三角形的内切圆
圆的外切三角形
三角形的内心
三角形三条角平分线的交点
名称 图形 确定方法 性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边
垂直平分线
的交点
1.OA=OB=OC
2.外心不一定在三角形的外部.
1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
o
A
B
C
O
A
B
C
三角形三条
角平分线的
交点
1.如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,
点O叫△ABC的 ,
它是三角形 的 交点.
外接
内接
外心
三边垂直平分线
2.如图2,△DEF是⊙I的 三角形,
⊙I是△DEF的 圆,
点I是 △DEF的 心,
它是三角形 的交点.
外切
内切
内
三条角平分线
A
B
C
O
.
图1
I
D
E
F
.
图2
按图填空
解:
∵点I是△ABC的内心,
∴ (∠1+ ∠2)
例1 如图,在△ABC中,∠A=68°,点I是内心,求∠BIC的度数.
A
B
C
I
)
1
(
2
4
(
∴ ∠1= ∠ABC.
3
)
同理 ∠2= ∠ACB.
= ( ∠ABC+ )
= ( 180° - ∠A )
= ( 180° - 68° )
= 56°
∠ACB
∴∠BIC= 180° - (∠1+ ∠2)
= 180°- 56°= 124°
如图,在△ABC中,∠A=68°,点I分别是两外角(图一)、一内角一外角(图二)的角平分线交点,
求∠BIC的度数.
图一
图二
∠I=56°
∠I=34°
68°
68°
2
1
3
4
2
1
4
3
挑战自我
1.已知△ABC的三边长分别为a,b,c,它的内切圆
半径为r,你会求△ABC的面积吗?
2.已知Rt△ABC的两直角边和斜边分别为a,b,C,你会求它的内切圆半径吗?
A
B
C
O●
┓
●
C
A
B
┐
●
┓
┓
.
A
B
C
a
b
c
r
r =
a+b-c
2
r
O
已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,求其内切圆O的半径长.
E
D
r
r
a-r
a-r
b-r+a-r=c
b-r
F
b-r
1. 通过类比三角形的外接圆与圆的内接三角形概念得出三角形的内切圆、圆的外切三角形概念.
2. 利用三角形内心的性质解题时,要注意整体思想和化整为零思想的运用.
课堂小结:
1.三角形的内切圆能作____个,圆的外切
三角形有_____ 个,三角形的内心在圆
的_______.
2.如图,O是△ABC的内心,则
(1)OA平分∠______, OB平分
∠______,OC平分∠______.
(2)若∠BAC=100°,则∠BOC=______.
1
无数
内部
C
O
B
A
BAC
140
ABC
ACB
3.直角三角形的两直角边分别5cm,12cm .则其内切圆的半径______。
.
A
B
C
O
2cm
达标检测
必做题:课本103页练习第2题
选做题:课本104页练习第5题
(2)若∠A=80 °,则∠BOC = 度.
(3)若∠BOC=100 °,则∠A = 度.
解:
130
20
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(20°+ 35 °) =125 °.
例1 如图,在△ABC中,点O是内心, (1)若∠ABC=40°, ∠ACB=70°,求∠BOC的度数.
A
B
C
O
)
1
(
3
4
(
∴ ∠1= ∠2= ∠ABC= ×40°= 20°.
2
)
同理 ∠3= ∠4= ∠ACB= ×70° =35 °.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
