5.1.1相交线[下学期]
图片预览




文档简介
课件20张PPT。相
交
线
课
件第
五
章
第
一
节相交线课件教学目标教学重点教学难点教学准备时间安排师生互动教学小结教学构想知识与能力数学思考解决问题情感态度与价值观思考题单击某项,出现相关解释,再单击该项,该解释消失。师生互动创设情景问题1:
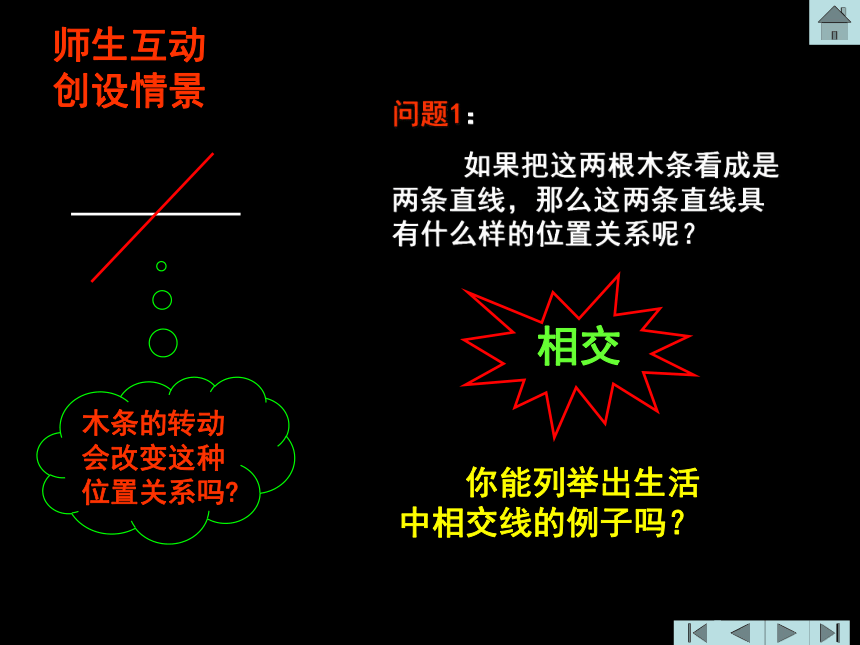
如果把这两根木条看成是两条直线,那么这两条直线具有什么样的位置关系呢? 你能列举出生活中相交线的例子吗?木条的转动会改变这种位置关系吗?师生互动创设情景其实现实生活中处处都有相交线,请看如下图片(共7张):问题2:
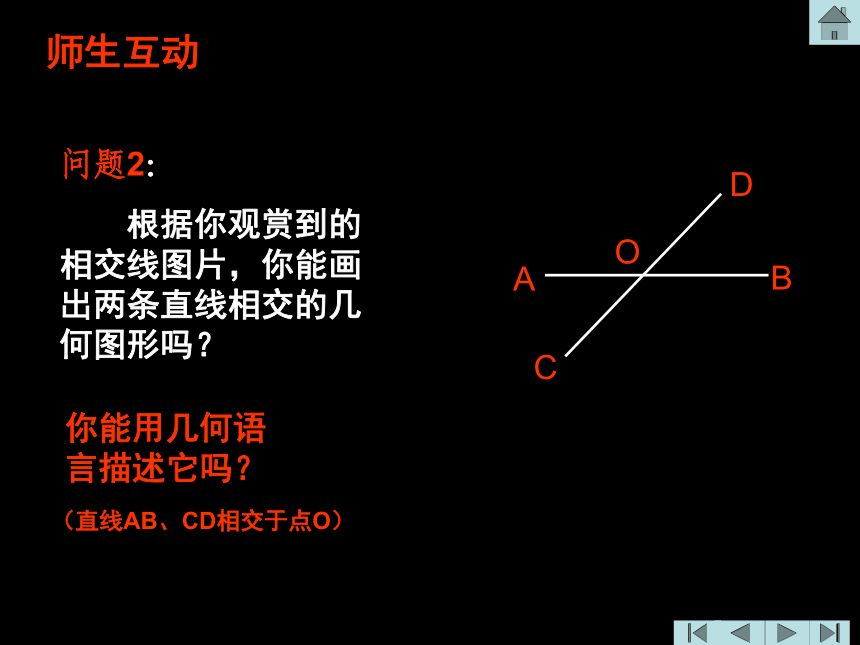
根据你观赏到的相交线图片,你能画出两条直线相交的几何图形吗?O师生互动你能用几何语言描述它吗?(直线AB、CD相交于点O)问题3:
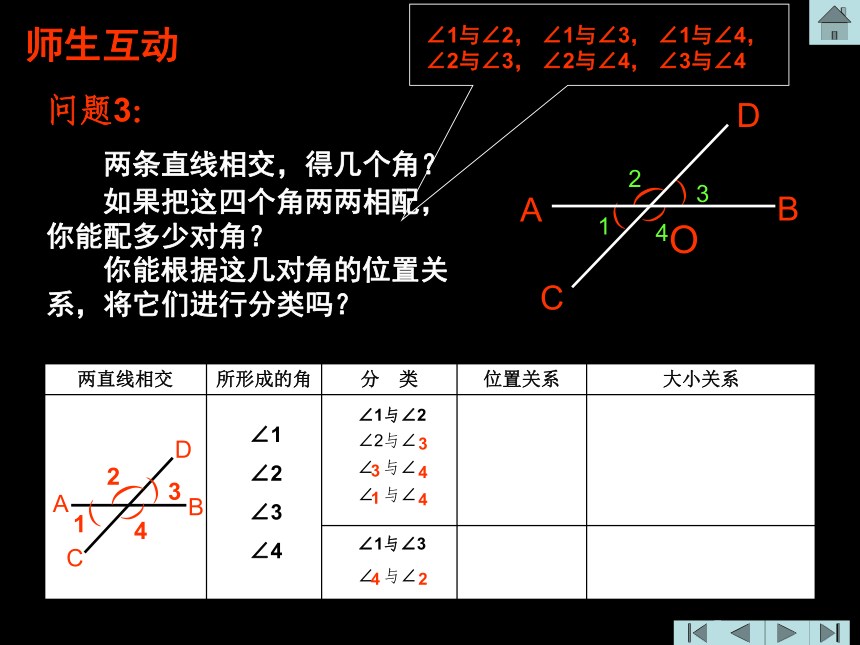
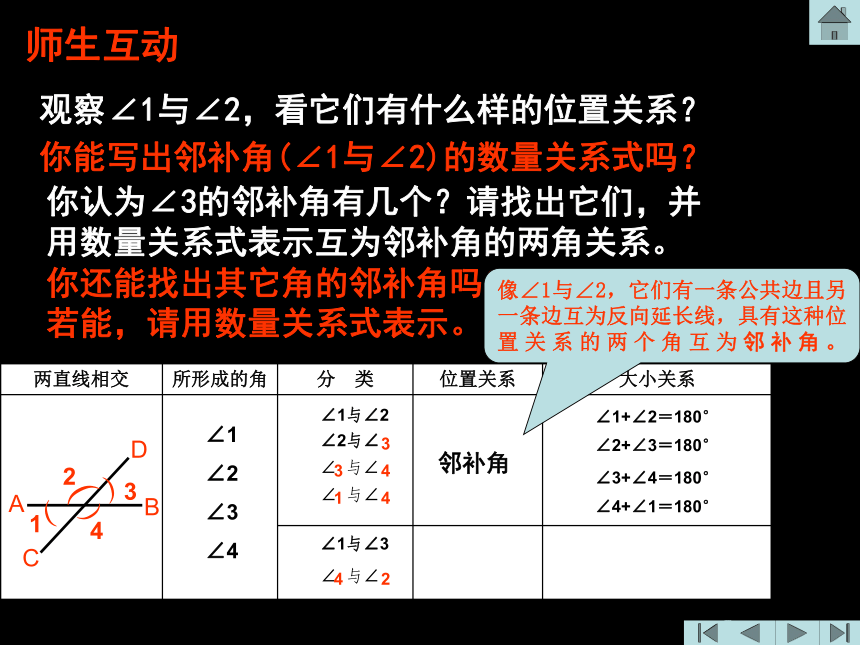
两条直线相交,得几个角? 如果把这四个角两两相配,你能配多少对角? 你能根据这几对角的位置关系,将它们进行分类吗?3344124师生互动观察∠1与∠2,看它们有什么样的位置关系?邻补角你认为∠3的邻补角有几个?请找出它们,并用数量关系式表示互为邻补角的两角关系。你还能找出其它角的邻补角吗?若能,请用数量关系式表示。像∠1与∠2,它们有一条公共边且另一条边互为反向延长线,具有这种位置关系的两个角互为邻补角。∠1+∠2=180°∠2+∠3=180°∠3+∠4=180°∠4+∠1=180°师生互动你能写出邻补角(∠1与∠2)的数量关系式吗?师生互动再观察∠1与∠3,看它们有什么样的位置关系?你从图中还能找到几对对顶角?像∠1与∠3,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角互为对顶角。对顶角对顶角请同学们用量角器度量一下∠1与∠3,观察它们的大小关系。师生互动∠1 = ∠3∠2与∠4相等吗? (可度量说明)∠2 = ∠4对顶角相等问题4:
你能用推理方法,书写出∠2=∠4吗? 为了验证度量结果∠1=∠3 的正确性,我们要用已学过的知识说明道理,怎样书写推理过程呢?解:因为∠1与∠2、∠1与∠4___________解:因为∠1与∠2、∠2与∠3____________所以∠1+∠2=______,∠2+∠3=_____又根据同角的补角相等得:__________所以∠1+∠2=______,∠1+∠4=_____又根据同角的补角相等得:___________师生互动互为邻补角思考:你还能写出不同的推理过程吗?180°180°∠1=∠3∠2=∠4180°180°互为邻补角选择题:1、下面哪个图中的∠1与∠2是对顶角?(2)没有公共顶点,并且一个角的两边也不是另一个角两边的反向延长线。虽有公共顶点,但∠2的两边不是∠1两边的反向延长线。没有公共顶点,不符合对顶角的定义。∠1与∠2符合对顶角的定义。师生互动 2、下列说法正确的是()
A、有公共顶点的角是对顶角
B、相等的两个角是对顶角
C、有公共点且相等的角是对顶角
D、两直线相交所成的四个角中,任意两 个角不是对顶角就是邻补角。答案:D师生互动 3:下列说法正确的是()
A、度数和是180°的两个角是邻补角
B、有公共点且互补的两个角是邻补角
C、一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
D、有公共顶点和一条公共边的两个角是邻补角答案:C师生互动 练习题:你能画出下图中∠1的对顶角和∠2的一个邻补角吗?师生互动轻松时刻谜底:对顶角知识应用培养能力 如下图,直线a、b相交,∠1=40°,求∠ 2、 ∠ 3、 ∠ 4的度数。解:因为 ∠1与∠2__________,且_________所以 ∠2=___________= __________=______ 又因为_________,所以∠3= ∠__= ___ , ∠2=∠_=______互为邻补角∠1=40°180 °-∠1140 °对顶角相等180 °- 40 °140 °140 °4 练习题:如图,直线AB、CD、EF相交于点O.
(1)写出∠AOC、∠BOE的邻补角;(2)写出∠DOA、∠EOC的对顶角;(3)如果∠AOC=50°,求 ∠BOD、
∠COB的度数;解:(1)∠AOC的邻补角为∠COB、∠AOD, (2)∠DOA的对顶角为∠COB,所以∠COB= 180 °-∠AOC=180-50°=130 °(师生互动(((∠BOE的邻补角为∠AOE、∠BOF ∠EOC的对顶角为∠DOF (3)因为∠AOC与∠BOD互为对顶角,且∠AOC=50°所以 ∠BOD=∠AOC=50°又因为∠AOC与∠COB互为邻补角,教学小结 1、对顶角与邻补角的概念、对顶角性质及其形成过程;3、从数形结合的思想方法的渗透过程中,体验数学来源于生活,同时又服务于生活。 2、能用几何语言描述简单的几何图形,并能对推理过程的每一步说明道理。本节课所学内容: 通过本节课的学习,你一定得到了很多启发, 请同学们谈谈你这节课有哪些收获?思考题 1、平面上两条直线相交,有几对对顶角,几对邻补角? 3、平面上有n条直线交于一点,如果每两条直线为一组,一共可组成多少组? 2、平面上三条直线交于一点,有几对对顶角,几对邻补角? 4、平面上 n 条直线相交于一点,有几对对顶角,几对邻补角?(2 对对顶角,4 对邻补角)(很显然,可形成6 对对顶角,12 对邻补角)由上题可知,n条直线相交于一点,两两组合可组成n(n-1)/2组。根据以上所学知识,n条直线相交于一点,有n(n-1)对对顶角2n(n-1)对邻补角反思 这节课我觉得很不错,就是后面的拓广有点难,学生不会把一个复杂的图形分解成几个基本的图形。
五
章
第
一
节相交线课件教学目标教学重点教学难点教学准备时间安排师生互动教学小结教学构想知识与能力数学思考解决问题情感态度与价值观思考题单击某项,出现相关解释,再单击该项,该解释消失。师生互动创设情景问题1:
如果把这两根木条看成是两条直线,那么这两条直线具有什么样的位置关系呢? 你能列举出生活中相交线的例子吗?木条的转动会改变这种位置关系吗?师生互动创设情景其实现实生活中处处都有相交线,请看如下图片(共7张):问题2:
根据你观赏到的相交线图片,你能画出两条直线相交的几何图形吗?O师生互动你能用几何语言描述它吗?(直线AB、CD相交于点O)问题3:
两条直线相交,得几个角? 如果把这四个角两两相配,你能配多少对角? 你能根据这几对角的位置关系,将它们进行分类吗?3344124师生互动观察∠1与∠2,看它们有什么样的位置关系?邻补角你认为∠3的邻补角有几个?请找出它们,并用数量关系式表示互为邻补角的两角关系。你还能找出其它角的邻补角吗?若能,请用数量关系式表示。像∠1与∠2,它们有一条公共边且另一条边互为反向延长线,具有这种位置关系的两个角互为邻补角。∠1+∠2=180°∠2+∠3=180°∠3+∠4=180°∠4+∠1=180°师生互动你能写出邻补角(∠1与∠2)的数量关系式吗?师生互动再观察∠1与∠3,看它们有什么样的位置关系?你从图中还能找到几对对顶角?像∠1与∠3,有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角互为对顶角。对顶角对顶角请同学们用量角器度量一下∠1与∠3,观察它们的大小关系。师生互动∠1 = ∠3∠2与∠4相等吗? (可度量说明)∠2 = ∠4对顶角相等问题4:
你能用推理方法,书写出∠2=∠4吗? 为了验证度量结果∠1=∠3 的正确性,我们要用已学过的知识说明道理,怎样书写推理过程呢?解:因为∠1与∠2、∠1与∠4___________解:因为∠1与∠2、∠2与∠3____________所以∠1+∠2=______,∠2+∠3=_____又根据同角的补角相等得:__________所以∠1+∠2=______,∠1+∠4=_____又根据同角的补角相等得:___________师生互动互为邻补角思考:你还能写出不同的推理过程吗?180°180°∠1=∠3∠2=∠4180°180°互为邻补角选择题:1、下面哪个图中的∠1与∠2是对顶角?(2)没有公共顶点,并且一个角的两边也不是另一个角两边的反向延长线。虽有公共顶点,但∠2的两边不是∠1两边的反向延长线。没有公共顶点,不符合对顶角的定义。∠1与∠2符合对顶角的定义。师生互动 2、下列说法正确的是()
A、有公共顶点的角是对顶角
B、相等的两个角是对顶角
C、有公共点且相等的角是对顶角
D、两直线相交所成的四个角中,任意两 个角不是对顶角就是邻补角。答案:D师生互动 3:下列说法正确的是()
A、度数和是180°的两个角是邻补角
B、有公共点且互补的两个角是邻补角
C、一条直线与端点在这条直线上的一条射线组成的两个角是邻补角
D、有公共顶点和一条公共边的两个角是邻补角答案:C师生互动 练习题:你能画出下图中∠1的对顶角和∠2的一个邻补角吗?师生互动轻松时刻谜底:对顶角知识应用培养能力 如下图,直线a、b相交,∠1=40°,求∠ 2、 ∠ 3、 ∠ 4的度数。解:因为 ∠1与∠2__________,且_________所以 ∠2=___________= __________=______ 又因为_________,所以∠3= ∠__= ___ , ∠2=∠_=______互为邻补角∠1=40°180 °-∠1140 °对顶角相等180 °- 40 °140 °140 °4 练习题:如图,直线AB、CD、EF相交于点O.
(1)写出∠AOC、∠BOE的邻补角;(2)写出∠DOA、∠EOC的对顶角;(3)如果∠AOC=50°,求 ∠BOD、
∠COB的度数;解:(1)∠AOC的邻补角为∠COB、∠AOD, (2)∠DOA的对顶角为∠COB,所以∠COB= 180 °-∠AOC=180-50°=130 °(师生互动(((∠BOE的邻补角为∠AOE、∠BOF ∠EOC的对顶角为∠DOF (3)因为∠AOC与∠BOD互为对顶角,且∠AOC=50°所以 ∠BOD=∠AOC=50°又因为∠AOC与∠COB互为邻补角,教学小结 1、对顶角与邻补角的概念、对顶角性质及其形成过程;3、从数形结合的思想方法的渗透过程中,体验数学来源于生活,同时又服务于生活。 2、能用几何语言描述简单的几何图形,并能对推理过程的每一步说明道理。本节课所学内容: 通过本节课的学习,你一定得到了很多启发, 请同学们谈谈你这节课有哪些收获?思考题 1、平面上两条直线相交,有几对对顶角,几对邻补角? 3、平面上有n条直线交于一点,如果每两条直线为一组,一共可组成多少组? 2、平面上三条直线交于一点,有几对对顶角,几对邻补角? 4、平面上 n 条直线相交于一点,有几对对顶角,几对邻补角?(2 对对顶角,4 对邻补角)(很显然,可形成6 对对顶角,12 对邻补角)由上题可知,n条直线相交于一点,两两组合可组成n(n-1)/2组。根据以上所学知识,n条直线相交于一点,有n(n-1)对对顶角2n(n-1)对邻补角反思 这节课我觉得很不错,就是后面的拓广有点难,学生不会把一个复杂的图形分解成几个基本的图形。
