2022-2023学年华东师大版八年级数学上册12.3.1 两数和乘以这两数的差 课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册12.3.1 两数和乘以这两数的差 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 20:48:43 | ||
图片预览








文档简介
(共23张PPT)
12.3 乘法公式
第12章 整式的乘除
1.两数和乘以这两数的差
学习目标
learning target
1.理解两数和乘以这两数差的几何意义.(重点)
2.理解并掌握两数和乘以这两数差的公式结构,并能正确运算.(难点)
多项式与多项式是如何相乘的?
(x + 2)( x + 3)
= x2+3x+2x+6
= x2+5x+6.
( a + b )( m + n )
= am
+ an
+ bm
+ bn
复习巩固
从前,有-个狡猾的地主,把-块边长为20 米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5 米,相邻的另-边增加 5 米,继续租给你,租金不变,你也没有吃亏,你看如何 ”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.你觉得张老汉是否吃亏了
情景导入
5米
5米
a米
原来
a2
(a - 5)
(a + 5)米
现在
(a + 5)(a - 5)
面积变了吗?
算一算:看谁算得又快又准.
计算下列多项式的积,你能发现什么规律?
① (a+ 1)( a - 1);
② (b+ 3)( m - 3);
③ (3m + 2)(3m - 2);
④ (6y + 2z)(6y - 2z).
想一想:
这些计算结果有什么特点?你发现了什么规律?
= a2 - 12
= b2 - 32
= (3m)2 - 22
两数和与这两数差的积,等于这两数的平方的差.
① (a+ 1)( a - 1) = a2 - 1
② (b + 3)( b - 3) = b2 - 9
③ (3m + 2)( 3m - 2) = 9m2 - 4
④ (6y +2z)(6y -2z) = 36y2 - 4z2
= (6y)2 – (2z)2
(a + b)(a b) = a2 b2.
两数和与这两数差的积等于这两数的平方差.这个公式叫做两数和与这两数差的乘法公式.有时也简称为平方差公式.
公式变形:
(b + a)( b + a ) = a2 b2
字母表达式:
平方差定义:
知识要点:
(a – b) (a + b) = a2 b2
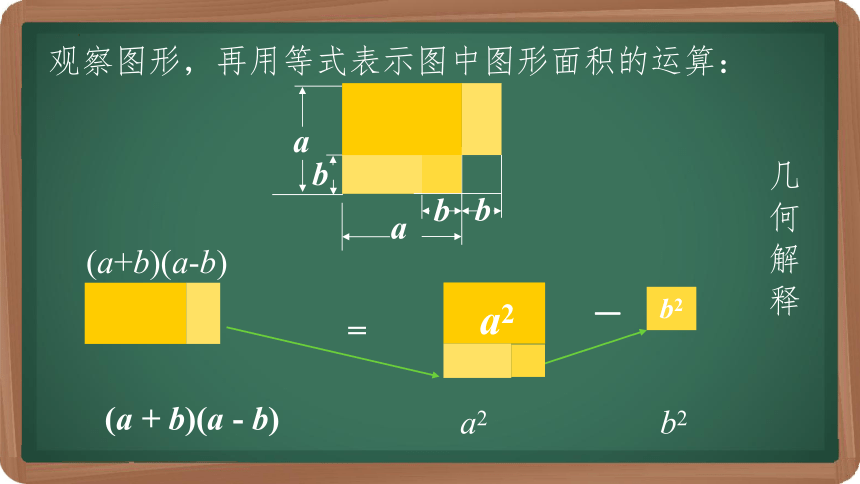
几 何 解 释
观察图形,再用等式表示图中图形面积的运算:
(a+b)(a-b)
=
-
(a + b)(a - b)
a2
b2
b
a
a
b
b
b2
a2
(a + b)(a - b) = a2 - b2
相同项为 a
相反项为 b
适当交换
合理加括号
平方差公式
注:这里的两数可以是两个单项式,也可以是两个多项式等.
练一练:
(l)(-a + b)(a + b) = _________.
(2)(a - b )(b + a) = __________.
(3)(-a - b)(-a + b) = ________.
(4)(a - b)(-a - b) = _________.
a2 - b2
a2 - b2
b2 - a2
b2 - a2
例1 填一填:
(2+ m)(2 - m)
( - 4 + b)( - 4 - b)
(0.6x - 2)(2 + 0.6x)
(3 + c)( - 3 + c)
a
b
a2 - b2
2
m
-4
b
22 - m2
( - 4)2 - b2
c
3
c2 - 32
0.6x
2
( 0.6x)2 - 22
(a - b)(a + b)
巩固应用
例2 计算 2017×2023.
(2020 - 3)(2020 + 3)
= 4080400 - 9
= 4080391.
解:原式=
= 20202 - 32
当式子中有三项或三项以上时,要仔细观察,找出相同项和相反项。
1. 下面各式的计算对不对?如果不对,应当怎样改正?
(1) (x + 2)(x - 2) = x2 - 2;
(2) ( 2a - 3)(-2a - 3) = 4a2 - 9.
不对
改正:x2 - 4
不对
改正方法①:
原式 = - [(2a + 3)(2a - 3)]
= - (4a2 - 9)
= - 4a2 + 9.
改正方法②:
原式 = ( - 3 - 2a)( - 3 + 2a)
= ( - 3)2 - (2a)2
= 9 - 4a2.
当堂练习
(1) (m + 2n)(m – 2n)
解:原式 = (3a + 1)(3a - 1)
= (3a)2 - 12
= 9a2 - 1
= m2 – 4n2
解:原式 = m2 - (2n)2
(3) (1 + 3a)(-1+ 3a)
2. 利用平方差公式计算:
(2) ( - 3x2 -2y)( - 3x2 +2y);
解:原式 = ( - 3x2 )2 – (2y)2
= 9x4 - 4y2
(4) ( - 4 + 3x)( - 3x - 4).
解:原式 = ( - 4 + 3x)( - 4 - 3x)
= ( - 4)2 - (3x)2
= 16 - 9x2
= (60 + 2)(60 – 2)
= 602 – 22
= 3600 – 4
= 3596.
= (9x2 - 4)
– (4x2 + 4x +1)
= 9x2 – 4–4x2 – 4x–1
(5)62×58;
(6)(3x + 2)(3x – 2) – (2x + 1) (2x +1).
= 5x2 –4x–5
先观察题目,然后根据题目特点选用合适的公式。
解:原式
解:原式
3.计算: 20222 - 2021×2023.
解:原式
= 20222 - (2022 - 1)(2022 + 1)
= 20222 - (20222 - 12 )
= 20222 - 20222 + 12
= 1.
4.利用平方差公式计算:
(1)(p - 2)(p+2)(p2 + 4)
解:原式 = (p2 - 4)(p2 + 4)
=p4 - 16
(2)(m+ n)(m - n)(m2 + n2)(m4 + n4).
解:原式 = (m2 - n2)(m2 + n2)(m4 + n4)
= (m4 - n4)(m4 + n4)
= m8 - n8
5.若实数m,n满足(m2+2n2+5)(m2+2n2﹣5)=0,则m2+2n2的值为( )
A.5 B.2.5 C.2.5或﹣5 D.5或﹣5
6.已知a﹣b=﹣2,则a2﹣b2+4b=______
A
4
7.观察下列等式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)= ;
…
(1)猜想规律:(x﹣1)(xn+xn﹣1+…+x2+x+1)= ;
(2)有以上情形,你能求出下面式子的结果吗?
(x6﹣1)÷(x﹣1)= ;
x4-1
xn+1-1
(3)已知x3+x2+x+1=0,分别求出x4和x2020的值.
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.字母表示:(a + b)(a - b) = a2 - b2
2.紧紧抓住 “一同一反”这一特征在应用时,只有两个二项式的积才有可能应用平方差公式;
3.不能直接应用公式的,要经过适当变形才可以应用
平方差公式
12.3 乘法公式
第12章 整式的乘除
1.两数和乘以这两数的差
学习目标
learning target
1.理解两数和乘以这两数差的几何意义.(重点)
2.理解并掌握两数和乘以这两数差的公式结构,并能正确运算.(难点)
多项式与多项式是如何相乘的?
(x + 2)( x + 3)
= x2+3x+2x+6
= x2+5x+6.
( a + b )( m + n )
= am
+ an
+ bm
+ bn
复习巩固
从前,有-个狡猾的地主,把-块边长为20 米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5 米,相邻的另-边增加 5 米,继续租给你,租金不变,你也没有吃亏,你看如何 ”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.你觉得张老汉是否吃亏了
情景导入
5米
5米
a米
原来
a2
(a - 5)
(a + 5)米
现在
(a + 5)(a - 5)
面积变了吗?
算一算:看谁算得又快又准.
计算下列多项式的积,你能发现什么规律?
① (a+ 1)( a - 1);
② (b+ 3)( m - 3);
③ (3m + 2)(3m - 2);
④ (6y + 2z)(6y - 2z).
想一想:
这些计算结果有什么特点?你发现了什么规律?
= a2 - 12
= b2 - 32
= (3m)2 - 22
两数和与这两数差的积,等于这两数的平方的差.
① (a+ 1)( a - 1) = a2 - 1
② (b + 3)( b - 3) = b2 - 9
③ (3m + 2)( 3m - 2) = 9m2 - 4
④ (6y +2z)(6y -2z) = 36y2 - 4z2
= (6y)2 – (2z)2
(a + b)(a b) = a2 b2.
两数和与这两数差的积等于这两数的平方差.这个公式叫做两数和与这两数差的乘法公式.有时也简称为平方差公式.
公式变形:
(b + a)( b + a ) = a2 b2
字母表达式:
平方差定义:
知识要点:
(a – b) (a + b) = a2 b2
几 何 解 释
观察图形,再用等式表示图中图形面积的运算:
(a+b)(a-b)
=
-
(a + b)(a - b)
a2
b2
b
a
a
b
b
b2
a2
(a + b)(a - b) = a2 - b2
相同项为 a
相反项为 b
适当交换
合理加括号
平方差公式
注:这里的两数可以是两个单项式,也可以是两个多项式等.
练一练:
(l)(-a + b)(a + b) = _________.
(2)(a - b )(b + a) = __________.
(3)(-a - b)(-a + b) = ________.
(4)(a - b)(-a - b) = _________.
a2 - b2
a2 - b2
b2 - a2
b2 - a2
例1 填一填:
(2+ m)(2 - m)
( - 4 + b)( - 4 - b)
(0.6x - 2)(2 + 0.6x)
(3 + c)( - 3 + c)
a
b
a2 - b2
2
m
-4
b
22 - m2
( - 4)2 - b2
c
3
c2 - 32
0.6x
2
( 0.6x)2 - 22
(a - b)(a + b)
巩固应用
例2 计算 2017×2023.
(2020 - 3)(2020 + 3)
= 4080400 - 9
= 4080391.
解:原式=
= 20202 - 32
当式子中有三项或三项以上时,要仔细观察,找出相同项和相反项。
1. 下面各式的计算对不对?如果不对,应当怎样改正?
(1) (x + 2)(x - 2) = x2 - 2;
(2) ( 2a - 3)(-2a - 3) = 4a2 - 9.
不对
改正:x2 - 4
不对
改正方法①:
原式 = - [(2a + 3)(2a - 3)]
= - (4a2 - 9)
= - 4a2 + 9.
改正方法②:
原式 = ( - 3 - 2a)( - 3 + 2a)
= ( - 3)2 - (2a)2
= 9 - 4a2.
当堂练习
(1) (m + 2n)(m – 2n)
解:原式 = (3a + 1)(3a - 1)
= (3a)2 - 12
= 9a2 - 1
= m2 – 4n2
解:原式 = m2 - (2n)2
(3) (1 + 3a)(-1+ 3a)
2. 利用平方差公式计算:
(2) ( - 3x2 -2y)( - 3x2 +2y);
解:原式 = ( - 3x2 )2 – (2y)2
= 9x4 - 4y2
(4) ( - 4 + 3x)( - 3x - 4).
解:原式 = ( - 4 + 3x)( - 4 - 3x)
= ( - 4)2 - (3x)2
= 16 - 9x2
= (60 + 2)(60 – 2)
= 602 – 22
= 3600 – 4
= 3596.
= (9x2 - 4)
– (4x2 + 4x +1)
= 9x2 – 4–4x2 – 4x–1
(5)62×58;
(6)(3x + 2)(3x – 2) – (2x + 1) (2x +1).
= 5x2 –4x–5
先观察题目,然后根据题目特点选用合适的公式。
解:原式
解:原式
3.计算: 20222 - 2021×2023.
解:原式
= 20222 - (2022 - 1)(2022 + 1)
= 20222 - (20222 - 12 )
= 20222 - 20222 + 12
= 1.
4.利用平方差公式计算:
(1)(p - 2)(p+2)(p2 + 4)
解:原式 = (p2 - 4)(p2 + 4)
=p4 - 16
(2)(m+ n)(m - n)(m2 + n2)(m4 + n4).
解:原式 = (m2 - n2)(m2 + n2)(m4 + n4)
= (m4 - n4)(m4 + n4)
= m8 - n8
5.若实数m,n满足(m2+2n2+5)(m2+2n2﹣5)=0,则m2+2n2的值为( )
A.5 B.2.5 C.2.5或﹣5 D.5或﹣5
6.已知a﹣b=﹣2,则a2﹣b2+4b=______
A
4
7.观察下列等式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)= ;
…
(1)猜想规律:(x﹣1)(xn+xn﹣1+…+x2+x+1)= ;
(2)有以上情形,你能求出下面式子的结果吗?
(x6﹣1)÷(x﹣1)= ;
x4-1
xn+1-1
(3)已知x3+x2+x+1=0,分别求出x4和x2020的值.
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.字母表示:(a + b)(a - b) = a2 - b2
2.紧紧抓住 “一同一反”这一特征在应用时,只有两个二项式的积才有可能应用平方差公式;
3.不能直接应用公式的,要经过适当变形才可以应用
平方差公式
